Matemática
O grande matemático Húngaro George Pólya $(1887 – 1985)$, recomendava um jeito divertido de se habituar aos fundamentos da matemática e de passar o tempo numa sala de espera de aeroporto ou de consultório médico: relembrar uma prova matemática já conhecida.
Vamos ver aqui, em notação moderna, a demonstração de Euclides sobre a existência de infinitos números primos, há cerca de $300$ anos antes de Cristo, em sua obra Os Elementos.
Números primos são maiores do que $1$ e só tem dois divisores: eles mesmos e o $1$. Por exemplo, o $19$ é primo, já o $60$ não é, pois é divisível por $12$ números inteiros.
Suponha um conjunto $A$ de número primos quaisquer:
\begin{equation*}
A={p_1, p_2, p_3, \cdots , p_n}
\end{equation*}
Suponha que o número $n$ seja o produto de todos os números primos do conjunto $A$:
\begin{equation*}
n = p_1 \cdot p_2 \cdot p_3 \cdot \cdots \cdot p_n
\end{equation*}
Suponha o número $q$ composto pelo número $n$ mais $1$:
\begin{equation*}
q = n+1
\end{equation*}
Se $q$ é um número primo, então existe um número primo fora do conjunto $A$. Se $q$ não é um número primo, então $q$ é divisível por um número primo $P_K$, já que todo número composto pode ser reduzido a um produto de números primos. Por exemplo:
\begin{equation*}
69 = 2^2 \cdot 3 \cdot 5
\end{equation*}
Se todo número composto é produto de números primos, então é divisível por qualquer um deles. Euclides disse que $P_K$ não pode estar dentro do conjunto $A$. Se estivesse, $P_K$ seria divisor de $n$ e de $q$ (que é $n + 1$).
Supondo que $P_K$ fosse divisor de $n$ e de $q$, teríamos:
\begin{gather}
q = n+1\\
\frac{n}{P_K} = i_1 \Longrightarrow n = P_K \cdot i_1\\
\frac{q}{P_K} = i_2 \Longrightarrow q = P_K \cdot i_2
\end{gather}
Nas relações $(2)$ e $(3)$, $i_1$ e $i_2$ são números inteiros e distintos um do outro. Substituindo $(1)$ na relação $(3)$, obtemos:
\begin{equation}
n+1 = P_K \cdot i_2
\end{equation}
E agora, substituímos $(2)$ na relação $(4)$:
\begin{equation*}
(P_K \cdot i_1) + 1 = P_K \cdot i_2\\
\ \\
i_2 = \frac{P_K \cdot i_1}{P_K} + \frac{1}{P_K}
\end{equation*}
\begin{equation}
i_2 = i_1 + \frac{1}{P_K}
\end{equation}
Se $q$ e $n$ são divisíveis por $P_K$, então $n$ dividido por $P_K$ dará o número inteiro $i_1$ e $q$ dividido por $P_K$ dará o número inteiro $i_2$. A relação $(5)$ diz que, para que o número $i_2$ seja inteiro é preciso que $1$ também seja divisível por $P_K$. Mas $1$ não é divisível por nenhum número primo, somente é divisível por si mesmo, caindo numa contradição.
Se $q$ não é um número primo, então, obrigatoriamente, $P_K$ está fora do conjunto $A$. A prova vale para qualquer conjunto de números primos, por mais completo que aparente ser: sempre haverá um número primo que não estará dentro do conjunto. Portanto, há infinitos números primos.
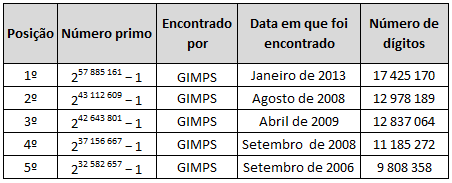
Poucas pessoas sabem de cor os números primos entre $1$ e $100$, e menos pessoas ainda sabem que o maior número primo atualmente conhecido foi descoberto em janeiro de $2013$ e possui $17$ milhões de algarismos:
\begin{equation*}
2^{57.885.161}-1
\end{equation*}
Mas mesmo sabendo tão pouco, graças a Euclides, podemos ter a certeza de que existem infinitos número primos
Um Diamante em Números
Dirichlet e os Números Primos de uma Progressão Aritmética
Construindo uma Sequência de Números Não-Primos

- A Desigualdade De Ptolomeu
Cláudio Ptolomeu foi um grande astrônomo e geômetra grego que viveu no século $I\ \text{d.C.}$. Neste post, provaremos uma desigualdade geométrica muito interessante. Proposição 1Dado o quadrilátero $ABCD$, onde $AC$ e $BD$ são as diagonais,...
- Sobre Os Primos Gêmeos
A conjectura dos números primos gêmeos afirma que existem infinitos números primos gêmeos, mas até hoje tal afirmação ainda não foi provada. Matemáticos acreditam que esta conjectura é verdadeira, baseado apenas nas evidências numéricas e...
- Demonstração Da Derivada Da Função Exponencial
Neste artigo, veremos como encontrar a derivada da função exponencial. Para isso utilizaremos limites e o conceito de derivada. Vamos demonstrar que, se $f(x)=e^x$, então sua derivada será $f '(x)=e^x$. Demonstração:Primeiramente, vamos provar...
- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...
- Demonstração Da Derivada Da Função Produto
A derivada de uma função pode ser representada geometricamente da seguinte maneira: Se $\Delta x$ for tão pequeno quanto quisermos, a reta que passa pelos pontos $[(x,f(x)),(x+\Delta x, f(x+\Delta x))]$, se confunde com a reta tangente no ponto $x$...
Matemática
A demonstração de Euclides sobre a existência de infinitos números primos
O grande matemático Húngaro George Pólya $(1887 – 1985)$, recomendava um jeito divertido de se habituar aos fundamentos da matemática e de passar o tempo numa sala de espera de aeroporto ou de consultório médico: relembrar uma prova matemática já conhecida.
Vamos ver aqui, em notação moderna, a demonstração de Euclides sobre a existência de infinitos números primos, há cerca de $300$ anos antes de Cristo, em sua obra Os Elementos.

[GIMPS: Great Internet Mersenne Prime Search]
Números primos são maiores do que $1$ e só tem dois divisores: eles mesmos e o $1$. Por exemplo, o $19$ é primo, já o $60$ não é, pois é divisível por $12$ números inteiros.
Suponha um conjunto $A$ de número primos quaisquer:
\begin{equation*}
A={p_1, p_2, p_3, \cdots , p_n}
\end{equation*}
Suponha que o número $n$ seja o produto de todos os números primos do conjunto $A$:
\begin{equation*}
n = p_1 \cdot p_2 \cdot p_3 \cdot \cdots \cdot p_n
\end{equation*}
Suponha o número $q$ composto pelo número $n$ mais $1$:
\begin{equation*}
q = n+1
\end{equation*}
Se $q$ é um número primo, então existe um número primo fora do conjunto $A$. Se $q$ não é um número primo, então $q$ é divisível por um número primo $P_K$, já que todo número composto pode ser reduzido a um produto de números primos. Por exemplo:
\begin{equation*}
69 = 2^2 \cdot 3 \cdot 5
\end{equation*}
Se todo número composto é produto de números primos, então é divisível por qualquer um deles. Euclides disse que $P_K$ não pode estar dentro do conjunto $A$. Se estivesse, $P_K$ seria divisor de $n$ e de $q$ (que é $n + 1$).
Supondo que $P_K$ fosse divisor de $n$ e de $q$, teríamos:
\begin{gather}
q = n+1\\
\frac{n}{P_K} = i_1 \Longrightarrow n = P_K \cdot i_1\\
\frac{q}{P_K} = i_2 \Longrightarrow q = P_K \cdot i_2
\end{gather}
Nas relações $(2)$ e $(3)$, $i_1$ e $i_2$ são números inteiros e distintos um do outro. Substituindo $(1)$ na relação $(3)$, obtemos:
\begin{equation}
n+1 = P_K \cdot i_2
\end{equation}
E agora, substituímos $(2)$ na relação $(4)$:
\begin{equation*}
(P_K \cdot i_1) + 1 = P_K \cdot i_2\\
\ \\
i_2 = \frac{P_K \cdot i_1}{P_K} + \frac{1}{P_K}
\end{equation*}
\begin{equation}
i_2 = i_1 + \frac{1}{P_K}
\end{equation}
Se $q$ e $n$ são divisíveis por $P_K$, então $n$ dividido por $P_K$ dará o número inteiro $i_1$ e $q$ dividido por $P_K$ dará o número inteiro $i_2$. A relação $(5)$ diz que, para que o número $i_2$ seja inteiro é preciso que $1$ também seja divisível por $P_K$. Mas $1$ não é divisível por nenhum número primo, somente é divisível por si mesmo, caindo numa contradição.
Se $q$ não é um número primo, então, obrigatoriamente, $P_K$ está fora do conjunto $A$. A prova vale para qualquer conjunto de números primos, por mais completo que aparente ser: sempre haverá um número primo que não estará dentro do conjunto. Portanto, há infinitos números primos.
Poucas pessoas sabem de cor os números primos entre $1$ e $100$, e menos pessoas ainda sabem que o maior número primo atualmente conhecido foi descoberto em janeiro de $2013$ e possui $17$ milhões de algarismos:
\begin{equation*}
2^{57.885.161}-1
\end{equation*}
Mas mesmo sabendo tão pouco, graças a Euclides, podemos ter a certeza de que existem infinitos número primos
Veja mais:
Os Elementos de EuclidesUm Diamante em Números
Dirichlet e os Números Primos de uma Progressão Aritmética
Construindo uma Sequência de Números Não-Primos

- A Desigualdade De Ptolomeu
Cláudio Ptolomeu foi um grande astrônomo e geômetra grego que viveu no século $I\ \text{d.C.}$. Neste post, provaremos uma desigualdade geométrica muito interessante. Proposição 1Dado o quadrilátero $ABCD$, onde $AC$ e $BD$ são as diagonais,...
- Sobre Os Primos Gêmeos
A conjectura dos números primos gêmeos afirma que existem infinitos números primos gêmeos, mas até hoje tal afirmação ainda não foi provada. Matemáticos acreditam que esta conjectura é verdadeira, baseado apenas nas evidências numéricas e...
- Demonstração Da Derivada Da Função Exponencial
Neste artigo, veremos como encontrar a derivada da função exponencial. Para isso utilizaremos limites e o conceito de derivada. Vamos demonstrar que, se $f(x)=e^x$, então sua derivada será $f '(x)=e^x$. Demonstração:Primeiramente, vamos provar...
- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...
- Demonstração Da Derivada Da Função Produto
A derivada de uma função pode ser representada geometricamente da seguinte maneira: Se $\Delta x$ for tão pequeno quanto quisermos, a reta que passa pelos pontos $[(x,f(x)),(x+\Delta x, f(x+\Delta x))]$, se confunde com a reta tangente no ponto $x$...
