Matemática
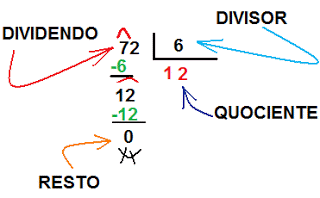 Fonte: Profº Francisco Valdir
Fonte: Profº Francisco Valdir
Blog Matemágicas e Numeros
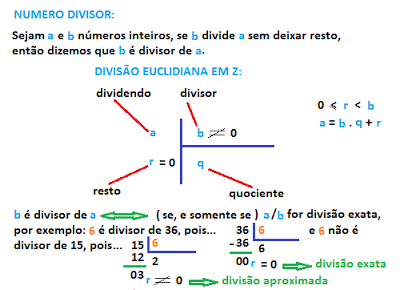




- Divisibilidade
Conhecer os critérios de divisibilidade facilita a resolução de cálculos envolvendo divisões. Vejamos alguns critérios de divisibilidade: DIVISIBILIDADE POR 2 Um número é divisível por 2 quando é par. Números pares são os que terminam em...
- Critérios De Divisibilidade
Conhecer os critérios de divisibilidade facilita a resolução de cálculos envolvendo divisões. Vejamos alguns critérios de divisibilidade: Divisibilidade por 2 Um número é divisível por 2 quando é par. Números pares são os que terminam...
- Critério De Divisibilidade
Critérios de divisibilidade Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se efetuar a divisão. Essas regras são chamadas de critérios de divisibilidade. Divisibilidade por...
- Divisibilidade
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
- Regra De Divisibilidade
Regras de divisibilidade Divisibilidade por 1 Todo número é divisível por 1. Divisibilidade por 2 Todos os números pares são divisíveis por 2, para isto basta terminarem em 0, 2, 4, 6 ou 8. Exemplo: 24 : 2 = 12 132 : 2 = 61 108 : 2 = 54 1024 :...
Matemática
A Divisibilidade Ajuda a Encontrar o 1600 Entre Números!!!

Blog Matemágicas e Numeros
Dado um número inteiro, segundo o Teorema Fundamental da Aritmética ele pode ser: simples ou composto. Diz-se que ele é simples se o conjunto de seus divisores é constituído ou formado por apenas dois divisores, a saber: a unidade e ele próprio, por exemplo: seja o número 19 que tem para divisor ( divisor é um número que divide outro exatamente) a unidade e ele, ou seja: o conjunto dos seus divisores é... D (19) = {1, 19} e nesse caso chamamos esse número de... número primo.

Um processo criado pelo grego Eratóstenes, chefe da biblioteca de Alexandria, nos permite encontrar vários números primos a partir do 2 e que ficou conhecido como o Crivo de Eratóstenes.

Começamos pelo número 2 (único número primo par que existe) vamos ao próximo número depois dele, o 3 e falamos... "um", em seguida falamos "dois" com o 4 que será riscado. Repetimos a fala "um" com o 5 e "dois" com o 6 que também será riscado e assim continua-se com... "um"... "dois" e rísca-se o tal, ou seja: todos os números pares serão riscados.
Passa-se a fazer o mesmo processo a partir do número 3, contando-se "um" no 4, "dois" no 5 e "três" no 6 que será riscado. Repetimos com "um" no 7, "dois" no 8 e três" com o 9 que também será riscado e continuamos aqui até o 99, quando repetimos o mesmo método a partir do número 5, depois o 7, 11, 13... ao final, os números que não foram riscados é porque pertencem ao conjunto dos números primos.

Não sendo primo, um número dado é chamado de... número composto, pois poderá ser obtido... pelo produto de vários números primos menores que ele. Assim, o conjunto de seus divisores além dele e da unidade, apresentará outros dos quais ele é múltiplo, por exemplo: O número 18 é um número composto pois se fizermos a sua fatoração encontraremos... 2 x 3² e assim o conjunto de seus divisores será... D (18) = {1, 2, 3, 6, 9, 18}.
Dado um certo número, saber achar todos os seus divisores é bom e é uma vantagem para o calculista que poderá lançar mão, para isso, do critério de divisibilidade (características e/ou resultados de operações ) ou do processo da fatoração isolada.
Vejamos os critérios da divisibilidade (desde o 2 até o 11):
Dado um número, por exemplo: 1420 podemos afirmar que ele é divisível por:
2 pois é um número par ( todos números os que terminam por: 0, 2, 4, 6 ou 8).
Não é divisível por 3, pois a soma dos algarismos que o forma... 1 + 4 + 2 + 0 = 7 e o 7 não é múltiplo de 3, portanto o 1420 também não será.
É divisível por 4, uma vez que os dois últimos algarismos da direita formam... 20 e o 20 é divisível por 4 (também, todos os números que terminam em 00), então, o 1420 também o será.
Será divisível por 5, pois todo numero que termina por 0 ou por 5 o são.
Também não será divisível por 6 devido não ser simultaneamente múltiplo de 2 e de 3.
Será divisível pelo 7? Vejamos um artifício: de 1420 tomamos o seu último algarismo na direita e o dobramos,assim... 0 x 2 = 0 , agora toma-se esse valor e subtrai-se da parte inteira do quociente... 1420 / 10 = 142. Assim... 142 ? 0 = 142 e se essa diferença der um múltiplo de 7 o número 1420 também seria divisível pelo 7 também, mas, percebemos que 142 não é múltiplo de 7, portanto, o 1420 também não o será. Para que não reste dúvida, se ao fazer as operações que deram o valor 142 e não se consegue ver se 142 é ou não é, um múltiplo de 7, então, a partir dele, mais uma vez podemos aplicar o artifício, i. É: 2 x2 = 4 depois a parte inteira do quociente... 142 / 10 = 14 e 14 ? 4 = 10 e como o 10 não é divisível por 7 assim podemos afirmar que o número 1420 também não é.
Um número é divisível por 8, se terminar por 000 ou os seus três últimos algarismos formarem um múltiplo de 8. O que é o caso de 1420, pois os seus três últimos algarismos da direita formam 420 que tem divisão exata pelo 8 e portanto, 1420 é divisível por 8.
1420 não tem divisão exata por 9 pois a soma... 1 + 4 + 2 + 0 = 7 dos seus algarismos ( como fizemos para o 3) não dão um número múltiplo de 9.
Todo número que termina por 0, é divisível por 10, portanto 1420 é múltiplo de 10.
Para saber se um número é divisível por 11, devemos achar as somas dos algarismos que se encontram nas ordens pares e fazemos o mesmo somando os valores colocados nas ordens ímpares, depois achamos a diferença entre essas somas e se derem um múltiplo de 11 é porque o número que foi dado também é divisível pelo 11. assim, o 1420 não é divisível por 11, pois: a soma dos algarismos nas ordens pares... 2 + 1 = 3 e a soma dos algarismos nas ordens ímpares... 0 + 4 = 4 dão a diferença... 4 ? 3 = 1 e como a diferença 1 não é múltipla de 11, impõe que o 1420 não é divisível por 11.
FATORAÇÃO ISOLADA:
Consiste em utilizar o dispositivo que se usa para encontrar os fatores primos de um número, traça-se linhas horizontais separando cada um dos fatores e acima do 1º colocamos o 1 e passamos a fazer o produto, de cima para baixo, de cada fator e colocamos o produto encontrado à sua direita caso ele não tenha sido ainda encontrado acima. Depois denotamos o conjunto dos seus divisores que começam pela unidade e terminam pelo próprio número. As imagens esclarecem todo o proceder:


- Divisibilidade
Conhecer os critérios de divisibilidade facilita a resolução de cálculos envolvendo divisões. Vejamos alguns critérios de divisibilidade: DIVISIBILIDADE POR 2 Um número é divisível por 2 quando é par. Números pares são os que terminam em...
- Critérios De Divisibilidade
Conhecer os critérios de divisibilidade facilita a resolução de cálculos envolvendo divisões. Vejamos alguns critérios de divisibilidade: Divisibilidade por 2 Um número é divisível por 2 quando é par. Números pares são os que terminam...
- Critério De Divisibilidade
Critérios de divisibilidade Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se efetuar a divisão. Essas regras são chamadas de critérios de divisibilidade. Divisibilidade por...
- Divisibilidade
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
- Regra De Divisibilidade
Regras de divisibilidade Divisibilidade por 1 Todo número é divisível por 1. Divisibilidade por 2 Todos os números pares são divisíveis por 2, para isto basta terminarem em 0, 2, 4, 6 ou 8. Exemplo: 24 : 2 = 12 132 : 2 = 61 108 : 2 = 54 1024 :...
