Matemática

A Equação do Número Prateado

Neste post veremos como encontrar a equação do número de prata, utilizando para isso proporções no retângulo prateado.

Definição $1$: O número prateado ou número de prata, ou ainda razão prateada, é uma constante irracional simbolizada por $\delta_S$ e numericamente vale:

\begin{equation}
\delta_S=1+\sqrt{2}
\end{equation}

Definição $2$: Um retângulo prateado é aquele cuja razão entre dois de seus lados adjacentes seja igual ao número prateado. Assim, tomando um retângulo de lados iguais a $AB$ e $AD$, a razão:
\begin{equation}
\frac{AB}{AD}=\delta_S=1+\sqrt{2}
\end{equation}
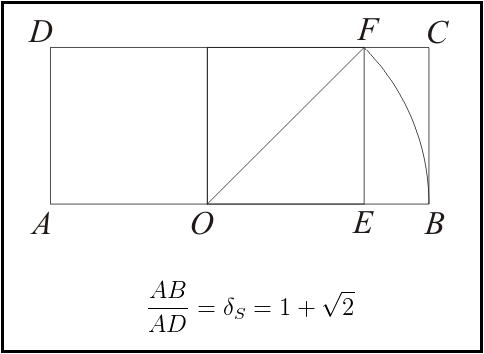
Partindo da construção geométrica do retângulo prateado, podemos deduzir a equação do número prateado. Considere o retângulo da figura acima. Pela definição de retângulo prateado, temos que a razão de prata é dada por:

\begin{equation}
\delta_S=\frac{AB}{AD}
\end{equation}

Usando semelhança de trângulos entre os retângulos $ABCD$ e $EBCF$, podemos deduzir que:

\begin{equation}
\frac{AD}{AB}=\frac{BE}{BC}
\end{equation}

No entanto, $BE=AB-2AD$, já que $AE=2AD$, e também $BC=AD$. Assim, podemos fazer estas substituições em $(4)$, obtendo:

\begin{equation}
\frac{AD}{AB}=\frac{AB-2AD}{AD}
\end{equation}

Mas, pela relação $(3)$, temos que $\delta_S=AB/AD$, e seu inverso será $\displaystyle \frac{1}{\delta_S}=\frac{AD}{AB}$. Assim:

\begin{equation}
\begin{matrix}
\frac{1}{\delta_S}=\frac{AB-2AD}{AD}\\
\frac{1}{\delta_S}=\frac{AB}{AD}-\frac{2AD}{AD}\\
\frac{1}{\delta_S}=\delta_S-2
\end{matrix}
\end{equation}

Multiplicando ambos os lados da equação por $\delta_S$ para eliminar o denominador:

\begin{equation}
1=\delta_S^2-2\delta_S
\end{equation}
E assim obtemos:
\begin{equation}
\delta_S^2-2\delta_S-1=0
\end{equation}

A equação obtida em $(8)$ é a equação do Número prateado. Podemos resolver esta equação utilizando a fórmula para a equação de segundo grau:

\begin{equation}
\begin{matrix}
\delta_S=\frac{2\pm \sqrt{8}}{2}\\
\delta_{S_1}=1+\sqrt{2}\\
\delta_{S_2}=1-\sqrt{2}
\end{matrix}
\end{equation}

Tomamos então a raiz positiva: $\delta_S=1+\sqrt{2}$ como solução da equação, encontrando o número prateado.

Veja mais:

O Número Prateado
O Retângulo Prateado
O Número Prateado na Trigonometria
O Número Prateado e a Área do Octógono Regular
Algumas Propriedades do Número Prateado no blog Fatos Matemáticos

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...

- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a}\ Dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq...

- Resolução Da Integral $\int \frac{1}{a\ E^{bx}}dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{a\ e^{bx}}dx = -\frac{e^{-bx}}{ab}+C \end{equation*} onde $a$ e $b \in \mathbb{R}$ e $a$ e $b \neq 0$. Seja a integral: \begin{equation*} I = \int \frac{1}{a\ e^{bx}}dx = \int \frac{e^{-bx}}{a}...

- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...

- A Equação Da Elipse
Consideremos num plano, dois pontos $F_1$ e $F_2$ distantes um do outro por $2c>0$ e seja $a>c$. Definição $1$:Elipse é o lugar geométrico dos pontos de um plano onde a soma das distâncias a dois pontos fixos desse plano é constante. Dá-se...

Matemática