Matemática
A função erro $erf(x)$ tem uma longa história que começa com os artigos de De Moivre $(1718-1733)$ e Laplace $(1774)$, onde foi expressa através da seguinte integral:$$\int e^{-t^2}dt$$
\begin{equation}
erf(x)=\frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}dt
\end{equation}
A função erro complementar é definida por:
\begin{equation}
erfc(x)=1-erf(x)=\frac{2}{\sqrt{\pi}}\int_x^\infty e^{-t^2}dt
\end{equation}
A função erro imaginário introduzida por Gauss é definida por:
\begin{equation}
erfi(z)=-ierf(iz)=-\frac{2i}{\sqrt{\pi}}\int_0^{iz}e^{-t^2}dt
\end{equation}
Fazemos uma mudança de variável:
$$t=iy \Rightarrow dt=idy$$
Vejam que na integral dada em $(3)$, $t$ assume valores de $0$ a $iz$ e com a mudança de variável, teremos que:
\begin{matrix}
\bullet &\text{ se } &t=0 &\Rightarrow &y=0\\
\bullet &\text{ se } &t=iz &\Rightarrow &iz=iy &\Rightarrow z=y
\end{matrix}
Obtemos então:
\begin{equation}
erfi(z)=-\frac{2i}{\sqrt{\pi}}\int_0^z e^{-(iy)^2}idy
\end{equation}
Como $i^2=-1$, temos:
\begin{equation}
erfi(z)=\frac{2}{\sqrt{\pi}}\int_0^z e^{y^2}dy
\end{equation}
Podemos expressar $(5)$ em termos de $t$:
\begin{equation}
erfi(z)=\frac{2}{\sqrt{\pi}}\int _0^z e^{t^2}dt
\end{equation}
Proposição 1: $\displaystyle \lim_{x \rightarrow +\infty}erf(x)=1$
Demonstração: Seja $I$ o limite acima. Assim:
\begin{equation}
\begin{matrix}
I=\lim_{x \rightarrow +\infty} erf(x)&=&\lim_{x \rightarrow +\infty}\frac{2}{\sqrt{\pi}}\int _0^xe^{-u^2}du\\
&=&\frac{2}{\sqrt{\pi}}\int _0^{+\infty}e^{-u^2}du
\end{matrix}
\end{equation}
e
\begin{equation}
\begin{matrix}
I=\lim_{x \rightarrow +\infty} erf(x)&=&\lim_{x \rightarrow +\infty}\frac{2}{\sqrt{\pi}}\int _0^xe^{-v^2}dv\\
&=&\frac{2}{\sqrt{\pi}}\int _0^{+\infty}e^{-v^2}dv
\end{matrix}
\end{equation} Multiplicando as expressões $(7)$ e $(8)$, obtemos:
\begin{equation}
\begin{matrix}
I^2&=&\frac{4}{\pi}\cdot \int_0^{+\infty}e^{-u^2}du \cdot \int_0^{+\infty} e^{-v^2}dv\\
&=&\frac{4}{\pi}\cdot \int_0^{+\infty}\int_0^{+\infty}e^{-u^2-v^2}dudv
\end{matrix}
\end{equation}
onde $J$ é o Jacobiano da transformação dado por:
$$J=\frac{\partial (u,v)}{\partial (r,\theta)}=\begin{vmatrix}
\frac{\partial u}{\partial r} & \frac{\partial u}{\partial \theta}\\
\\
\frac{\partial v}{\partial r} & \frac{\partial v}{\partial \theta}
\end{vmatrix} =\begin{vmatrix}
\cos(\theta) & -r\text{sen}(\theta)\\
\\
\text{sen}(\theta) & r\cos(\theta)
\end{vmatrix} = r\cos^2(\theta)+r\text{sen}^2(\theta)=r$$
Assim, $dudv=rdrd\theta$, de modo que:
\begin{matrix}
I^2&=& \frac{4}{\pi}\int_0^{\pi/2}\int_0^{+\infty}e^{-r^2}\cdot rdrd\theta\\
&=& \frac{4}{\pi}\int_0^{\pi/2}d\theta \cdot \lim_{p \rightarrow +\infty}\int_0^pe^{-r^2}\cdot rdr\\
&=&\frac{4}{\pi}\cdot \frac{\pi}{2}\cdot \lim_{p \rightarrow +\infty}\left[-\frac{1}{2}e^{-r^2}\right]_0^p\\
&=&2\cdot \lim_{p \rightarrow +\infty} \left[-\frac{1}{2}e^{-p^2}+\frac{1}{2}\right]\Rightarrow\\
\end{matrix} $$I^2=1\Rightarrow I=1$$
Corolário $1$: $\displaystyle \lim_{x \rightarrow -\infty}erf(x)=1$
Demonstração:
$$\lim_{x \rightarrow -\infty}erf(x)=\lim_{y \rightarrow +\infty}erf(-y)=\lim_{y \rightarrow +\infty}erf(y)=1$$
$y=-x$. Se $x \rightarrow -\infty$, então $y\rightarrow +\infty$.
No penúltimo passo, usamos o fato de que a função $erf(x)$ é par.
Exemplo $1$: A função gama denotada por $\Gamma(x)$ é definida por:
$$\Gamma(x)=\int_0^{+\infty}t^{x-1}e^{-t}dt\text{ , }x>0$$
Mostre que $\Gamma (1/2)=\sqrt{\pi}$.
Façamos $t=u^2$ na integral acima. Note que $dt=2udu$ e que os limites de integração são os mesmo. Assim:
$$\Gamma(1/2)=\int_0^{+\infty}(u^2)^{\frac{1}{2}-1}e^{-u^2}\cdot 2udu$$
$$\Gamma(1/2)=2\cdot \int_0^{+\infty}u^{-1}\cdot e^{-u^2}\cdot udu$$
$$\Gamma(1/2)=2\cdot \int_0^{+\infty}e^{-u^2}du$$
$$\Gamma(1/2)=\sqrt{\pi}\cdot \frac{2}{\sqrt{\pi}}\int_0^{+\infty}e^{-u^2}du$$
$$\Gamma(1/2)=\sqrt{\pi} \cdot \lim_{p \rightarrow +\infty}\frac{2}{\sqrt{\pi}}\int_0^pe^{-u^2}du$$
$$\Gamma(1/2)=\sqrt{\pi} \cdot \lim_{p \rightarrow +\infty}erf(p)=\sqrt{\pi}\cdot 1=\sqrt{\pi}$$
Aplicamos o método de integração por partes, de modo que:
$$u=x \Rightarrow \frac{du}{dx}=1 \Rightarrow du=dx$$
e
$$dv=xe^{x^2}dx \Rightarrow v=\frac{e^{x^2}}{2}$$
Seja $u=x^2$ e $du=2xdx$. Assim:
\begin{matrix}
dv=xe^{x^2}dx \Rightarrow &v&=\int xe^{x^2}dx\\
&v&=\int \frac{xe^u}{2x}du\\
&v&=\frac{1}{2}\int e^udu\\
\end{matrix}
Como a integral de $e^u=e^u$, temos:
\begin{matrix}
v&=&\frac{1}{2}e^u+C\\
v&=&\frac{e^u}{2}+C\\
v&=&\frac{e^{x^2}}{2}+C\\
\end{matrix}
Retomando as ideias, temos pela integração por partes que:
$$\int udv=uv-\int vdu$$
Assim:
$$\int x^2e^{x^2}dx=x\cdot \frac{e^{x^2}}{2}-\int \frac{e^{x^2}}{2}\cdot dx+C$$
$$\int x^2e^{x^2}dx=\frac{xe^{x^2}}{2}-\frac{1}{2}\int e^{x^2} dx+C$$
$$\int x^2e^{x^2}dx=\frac{xe^{x^2}}{2}-\frac{1}{2}\cdot \frac{\sqrt{\pi}}{2}\cdot \frac{2}{\sqrt{\pi}}\int e^{x^2} dx+C$$
\begin{equation}
\int x^2e^{x^2}dx=\frac{xe^{x^2}}{2}-\frac{\sqrt{\pi}}{4} erfi(x)+C
\end{equation}
Veja mais:
Método de Integração por Partes
Método de Integração por Substituição
Sobre as Funções Gama e Beta Partes: 1, 2, 3 e 4 no blog Fatos Matemáticos
Versões Discretas da Transformada de Laplace e da Função Gama no blog Elementos

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integrais Impróprias Com Limites Finitos
Quando escrevemos uma integral definida como: \begin{equation} \int_a^b f(x)dx \end{equation} admitimos que o limite de integração são números finitos e que o integrando $f(x)$ é uma função contínua no intervalo limitado $a \leq x \leq b$. Sua...
- Teste Da Integral Para Convergência De Séries
O teorema conhecido como teste da integral (ou teste de Leibniz) para verificar convergências de séries, faz uso da teoria de integrais impróprias. Teorema $1$:Se $f(n)$ representa o termo geral $u_n$ de uma série numérica infinita de termos positivos,...
- Demonstração Do Limite Fundamental Exponencial
O número e tem grande importância em diversos ramos das ciências, pois está presente em vários fenômenos naturais como por exemplo: crescimento populacional, crescimento de população de bactérias, datação por carbono, circuitos elétricos,...
Matemática
A Função Erro e Outras Funções Relacionadas
Por:
Kleber Kilhian
Paulo Sérgio Costa Lino
A função erro $erf(x)$ tem uma longa história que começa com os artigos de De Moivre $(1718-1733)$ e Laplace $(1774)$, onde foi expressa através da seguinte integral:
Mais tarde, Kramp $(1799)$ utilizou esta integral para a definição da função de erro complementar $erfc(x)$.
A integral de probabilidade foi assim chamada porque é amplamente utilizada na teoria da probabilidade e estatística, aparecendo também em equações diferenciais parciais.
A função erro imaginário $erfi(z)$ também chamada de Função Erro de Gauss, foi desenvolvida para calcular a integral da distribuição normal. Gauss mostrou como a probabilidade pode ser representada por uma curva em forma de sino ou normal, onde o erro se distribui simetricamente com picos na média e caindo rapidamente para mais e menos infinito. Em $1809$, Gauss usou esta função para analisar dados astronômicos.
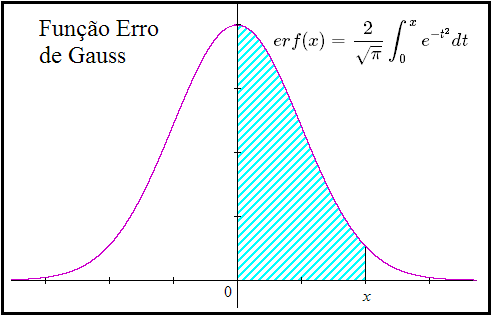
A função erro é definida por:\begin{equation}
erf(x)=\frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}dt
\end{equation}
A função erro complementar é definida por:
\begin{equation}
erfc(x)=1-erf(x)=\frac{2}{\sqrt{\pi}}\int_x^\infty e^{-t^2}dt
\end{equation}
A função erro imaginário introduzida por Gauss é definida por:
\begin{equation}
erfi(z)=-ierf(iz)=-\frac{2i}{\sqrt{\pi}}\int_0^{iz}e^{-t^2}dt
\end{equation}
Fazemos uma mudança de variável:
$$t=iy \Rightarrow dt=idy$$
Vejam que na integral dada em $(3)$, $t$ assume valores de $0$ a $iz$ e com a mudança de variável, teremos que:
\begin{matrix}
\bullet &\text{ se } &t=0 &\Rightarrow &y=0\\
\bullet &\text{ se } &t=iz &\Rightarrow &iz=iy &\Rightarrow z=y
\end{matrix}
Obtemos então:
\begin{equation}
erfi(z)=-\frac{2i}{\sqrt{\pi}}\int_0^z e^{-(iy)^2}idy
\end{equation}
Como $i^2=-1$, temos:
\begin{equation}
erfi(z)=\frac{2}{\sqrt{\pi}}\int_0^z e^{y^2}dy
\end{equation}
Podemos expressar $(5)$ em termos de $t$:
\begin{equation}
erfi(z)=\frac{2}{\sqrt{\pi}}\int _0^z e^{t^2}dt
\end{equation}
Proposição 1: $\displaystyle \lim_{x \rightarrow +\infty}erf(x)=1$
Demonstração: Seja $I$ o limite acima. Assim:
\begin{equation}
\begin{matrix}
I=\lim_{x \rightarrow +\infty} erf(x)&=&\lim_{x \rightarrow +\infty}\frac{2}{\sqrt{\pi}}\int _0^xe^{-u^2}du\\
&=&\frac{2}{\sqrt{\pi}}\int _0^{+\infty}e^{-u^2}du
\end{matrix}
\end{equation}
e
\begin{equation}
\begin{matrix}
I=\lim_{x \rightarrow +\infty} erf(x)&=&\lim_{x \rightarrow +\infty}\frac{2}{\sqrt{\pi}}\int _0^xe^{-v^2}dv\\
&=&\frac{2}{\sqrt{\pi}}\int _0^{+\infty}e^{-v^2}dv
\end{matrix}
\end{equation} Multiplicando as expressões $(7)$ e $(8)$, obtemos:
\begin{equation}
\begin{matrix}
I^2&=&\frac{4}{\pi}\cdot \int_0^{+\infty}e^{-u^2}du \cdot \int_0^{+\infty} e^{-v^2}dv\\
&=&\frac{4}{\pi}\cdot \int_0^{+\infty}\int_0^{+\infty}e^{-u^2-v^2}dudv
\end{matrix}
\end{equation}
Observe que a região de integração é o $1^\circ$ quadrante. Para resolver a integral dupla $(9)$, De Moivre teve a ideia de usar coordenadas polares, fazendo $u=r\cos (\theta)$ e $v=r \text{sen}(\theta)$. O elemento de área $dudv$ está relacionado com o elemento $drd\theta$ através da expressão:
$$dudv=\left | J \right |drd \theta$$onde $J$ é o Jacobiano da transformação dado por:
$$J=\frac{\partial (u,v)}{\partial (r,\theta)}=\begin{vmatrix}
\frac{\partial u}{\partial r} & \frac{\partial u}{\partial \theta}\\
\\
\frac{\partial v}{\partial r} & \frac{\partial v}{\partial \theta}
\end{vmatrix} =\begin{vmatrix}
\cos(\theta) & -r\text{sen}(\theta)\\
\\
\text{sen}(\theta) & r\cos(\theta)
\end{vmatrix} = r\cos^2(\theta)+r\text{sen}^2(\theta)=r$$
Assim, $dudv=rdrd\theta$, de modo que:
\begin{matrix}
I^2&=& \frac{4}{\pi}\int_0^{\pi/2}\int_0^{+\infty}e^{-r^2}\cdot rdrd\theta\\
&=& \frac{4}{\pi}\int_0^{\pi/2}d\theta \cdot \lim_{p \rightarrow +\infty}\int_0^pe^{-r^2}\cdot rdr\\
&=&\frac{4}{\pi}\cdot \frac{\pi}{2}\cdot \lim_{p \rightarrow +\infty}\left[-\frac{1}{2}e^{-r^2}\right]_0^p\\
&=&2\cdot \lim_{p \rightarrow +\infty} \left[-\frac{1}{2}e^{-p^2}+\frac{1}{2}\right]\Rightarrow\\
\end{matrix} $$I^2=1\Rightarrow I=1$$
Observação: Os limites de integração foram $0\leq\theta\leq\pi/2$ e $0\leq r <+\infty$, pois desta forma, preenchemos o $1^\circ$ quadrante, que é a região de integração das variáveis antigas.
Corolário $1$: $\displaystyle \lim_{x \rightarrow -\infty}erf(x)=1$
Demonstração:
$$\lim_{x \rightarrow -\infty}erf(x)=\lim_{y \rightarrow +\infty}erf(-y)=\lim_{y \rightarrow +\infty}erf(y)=1$$
$y=-x$. Se $x \rightarrow -\infty$, então $y\rightarrow +\infty$.
No penúltimo passo, usamos o fato de que a função $erf(x)$ é par.
Exemplo $1$: A função gama denotada por $\Gamma(x)$ é definida por:
$$\Gamma(x)=\int_0^{+\infty}t^{x-1}e^{-t}dt\text{ , }x>0$$
Mostre que $\Gamma (1/2)=\sqrt{\pi}$.
Façamos $t=u^2$ na integral acima. Note que $dt=2udu$ e que os limites de integração são os mesmo. Assim:
$$\Gamma(1/2)=\int_0^{+\infty}(u^2)^{\frac{1}{2}-1}e^{-u^2}\cdot 2udu$$
$$\Gamma(1/2)=2\cdot \int_0^{+\infty}u^{-1}\cdot e^{-u^2}\cdot udu$$
$$\Gamma(1/2)=2\cdot \int_0^{+\infty}e^{-u^2}du$$
$$\Gamma(1/2)=\sqrt{\pi}\cdot \frac{2}{\sqrt{\pi}}\int_0^{+\infty}e^{-u^2}du$$
$$\Gamma(1/2)=\sqrt{\pi} \cdot \lim_{p \rightarrow +\infty}\frac{2}{\sqrt{\pi}}\int_0^pe^{-u^2}du$$
$$\Gamma(1/2)=\sqrt{\pi} \cdot \lim_{p \rightarrow +\infty}erf(p)=\sqrt{\pi}\cdot 1=\sqrt{\pi}$$
Exemplo $2$: Vamos calcular a integral $\displaystyle \int x^2 e^{x^2}dx$. Temos que:
$$\int x^2e^{x^2}dx=\int x \cdot xe^{x^2}dx$$Aplicamos o método de integração por partes, de modo que:
$$u=x \Rightarrow \frac{du}{dx}=1 \Rightarrow du=dx$$
e
$$dv=xe^{x^2}dx \Rightarrow v=\frac{e^{x^2}}{2}$$
Observação: Para integrarmos $\displaystyle dv=xe^{x^2}dx$, aplicamos o método de integração por substituição.
Seja $u=x^2$ e $du=2xdx$. Assim:
\begin{matrix}
dv=xe^{x^2}dx \Rightarrow &v&=\int xe^{x^2}dx\\
&v&=\int \frac{xe^u}{2x}du\\
&v&=\frac{1}{2}\int e^udu\\
\end{matrix}
Como a integral de $e^u=e^u$, temos:
\begin{matrix}
v&=&\frac{1}{2}e^u+C\\
v&=&\frac{e^u}{2}+C\\
v&=&\frac{e^{x^2}}{2}+C\\
\end{matrix}
Retomando as ideias, temos pela integração por partes que:
$$\int udv=uv-\int vdu$$
Assim:
$$\int x^2e^{x^2}dx=x\cdot \frac{e^{x^2}}{2}-\int \frac{e^{x^2}}{2}\cdot dx+C$$
$$\int x^2e^{x^2}dx=\frac{xe^{x^2}}{2}-\frac{1}{2}\int e^{x^2} dx+C$$
$$\int x^2e^{x^2}dx=\frac{xe^{x^2}}{2}-\frac{1}{2}\cdot \frac{\sqrt{\pi}}{2}\cdot \frac{2}{\sqrt{\pi}}\int e^{x^2} dx+C$$
\begin{equation}
\int x^2e^{x^2}dx=\frac{xe^{x^2}}{2}-\frac{\sqrt{\pi}}{4} erfi(x)+C
\end{equation}
Veja mais:
Método de Integração por Partes
Método de Integração por Substituição
Sobre as Funções Gama e Beta Partes: 1, 2, 3 e 4 no blog Fatos Matemáticos
Versões Discretas da Transformada de Laplace e da Função Gama no blog Elementos

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integrais Impróprias Com Limites Finitos
Quando escrevemos uma integral definida como: \begin{equation} \int_a^b f(x)dx \end{equation} admitimos que o limite de integração são números finitos e que o integrando $f(x)$ é uma função contínua no intervalo limitado $a \leq x \leq b$. Sua...
- Teste Da Integral Para Convergência De Séries
O teorema conhecido como teste da integral (ou teste de Leibniz) para verificar convergências de séries, faz uso da teoria de integrais impróprias. Teorema $1$:Se $f(n)$ representa o termo geral $u_n$ de uma série numérica infinita de termos positivos,...
- Demonstração Do Limite Fundamental Exponencial
O número e tem grande importância em diversos ramos das ciências, pois está presente em vários fenômenos naturais como por exemplo: crescimento populacional, crescimento de população de bactérias, datação por carbono, circuitos elétricos,...
