Matemática
No século $XVII$, pouco antes da invenção do Cálculo Diferencial e Integral, existiam muitos métodos para os problemas de quadratura (cálculo de áreas), cubatura e retificação de uma curva.
O problema de calcular o comprimento de arco de uma curva é em alguns casos extremamente difícil, pois pode nos levar a integrais elípticas. Com a invenção do Cálculo Diferencial e Integral, este procedimento nos leva a resolução de uma integral definida em que o integrando envolve uma raiz quadrada e a derivada da função dada.
Para curvas geradas por funções do primeiro grau, basta aplicarmos o Teorema pitagórico no intervalo desejado que encontramos o comprimento da curva rapidamente.

O segmento $\ell$ é a hipotenusa do triângulo retângulo de catetos $\Delta x$ e $\Delta y$ e seu comprimento é dado por:
\begin{equation}
\ell = \sqrt{\Delta x^2 + \Delta y^2}
\end{equation}
Para as demais funções, temos que usar o Cálculo para determinarmos o comprimento desejado de um arco.
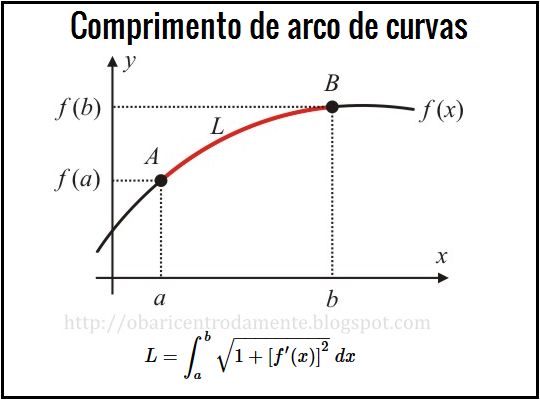
Considere a função $y=f(x)$, contínua no intervalo $[a,b]$ e derivável em $(a,b)$, cujo gráfico pode ser esboçado como:

Para determinarmos o comprimento do arco da curva entre os pontos $A=\left(a,f(a)\right)$ e $B=\left(b, f(b)\right)$, podemos subdividir a curva em segmentos infinitesimais de reta, que já sabemos calcular pela relação $(1)$, onde:
\begin{equation*}
x_0 = a < x_1 <x_2 < \cdots < x_{k-1} < x_k < \cdots < x_n = b
\end{equation*}
Conforme podemos observar na figura abaixo:

Seja $P_k$ o ponto $(x_k , y_k)$ onde $y_k = f(x_k)$. O comprimento total da poligonal $P_0P_1P_2\cdots P_{k-1}P_k\cdots P_n$ é a soma dos comprimentos das cordas que ligam cada ponto ao próximo.
Sejam $\Delta x_k = x_k - x_{k-1}$ e $\Delta y_k = y_k - y_{k-1}$ para $k=1,2,3, \cdots, n$.
Assim, temos triângulos retângulos e o problema se resumiria em encontrarmos os comprimentos infinitesimais de suas hipotenusas de tamanho $\ell_k$:

Pelo teorema pitagórico, o comprimento da k-ésima corda, denotada por $\ell _k$, é igual a:
\begin{equation*}
\ell_k = \sqrt{\left(\Delta x_k \right)^2 + \left(\Delta y_k \right)^2}\\
\ \\
\ell_k = \sqrt{\frac{\left(\Delta x_k \right)^2 + \left(\Delta y_k \right)^2}{\left(\Delta x_k \right)^2}\cdot \left(\Delta x_k \right)^2}\\
\ \\
\ell_k = \sqrt{1+\frac{\left(\Delta y_k \right)^2}{\left(\Delta x_k \right)^2}} \cdot \Delta x_k
\end{equation*}
\begin{equation}
\ell_k = \sqrt{1 + \left( \frac{\Delta y_k}{\Delta x_k}\right)^2} \Delta x_k
\end{equation}
Considerando $f(x)$ contínua no intervalo $[a,b]$ e derivável em $(a,b)$, então $f(x)$ é derivável no intervalo $[x_{k-1}, x_k]$ e pelo teorema do valor médio, existe $\xi_k \in (x_{k-1}, x_k)$, tal que:
\begin{equation}
\frac{\Delta y_k}{\Delta x_k} = f^{\prime} (\xi _k)
\end{equation}
Substituindo $(3)$ em $(2)$, temos que:
\begin{equation}
\ell _k = \sqrt{1+ \left[ f^{\prime} (\xi _k)\right]^2} \cdot \Delta x_k
\end{equation}
Mas, $\ell_k$ é somente o comprimento de um segmento infinitesimal da curva. Para o comprimento total da poligonal $L$, fazemos:
\begin{equation*}
L = \sum_{k=1}^n \ell_k = \sum_{k=1}^n \sqrt{1+\left[ f^{\prime} (\xi_k)\right]^2} \cdot \Delta x_k
\end{equation*}
Quando tende ao infinito, o comprimento do subintervalo tende a zero. Assim, se $L$ denota o comprimento do arco $AB$, então:
\begin{equation*}
L = \lim_{\max \Delta x_k \rightarrow 0} \sum_{k=1}^n \sqrt{1+ \left[ f^{\prime}(\xi _k)\right]^2} \cdot \Delta x_k
\end{equation*}
\begin{equation}
L = \int_a^b \sqrt{1+\left[ f^{\prime} (x) \right]^2} \ dx
\end{equation}
Isso com a hipótese adicional que $f^{\prime} (x)$ seja contínua para que a integral dada na relação $(5)$ exista.
Vejamos alguns exemplos para melhor ilustrar esta ideia.
Primeiramente calculamos a derivada da função:
\begin{equation*}
f(x) = 2x-1 \quad \Longrightarrow \quad f^{\prime}(x)=2
\end{equation*}
Em seguida, substituímos na fórmula $(5)$ para o comprimento do arco:
\begin{equation*}
L=\int_1^2 \sqrt{1+(2)^2}\ dx = \int_1^2 \sqrt{5}\ dx = \left[\sqrt{5} x\right]_1^2=\sqrt{5}~~u.c.
\end{equation*}
Graficamente temos:

Se utilizarmos o teorema pitagórico, obteríamos:
\begin{equation*}
L^2 = (3-1)^2 +(2-1)^2 \\
L=\sqrt{5}~~u.c.
\end{equation*}
Que é exatamente o que encontramos utilizando o cálculo diferencial e integral.
Podemos aplicar este conceito para diversas curvas mais complexas, mas dependendo da função original, podemos obter uma integral com bastante dificuldade de resolução. Vejamos outro exemplo:

A função $f(x)=x^{3/2}$ tem como derivada $f^{\prime}(x)= \frac{3}{2}x^{1/2}$. Aplicamos a fórmula dada em $(5)$:
\begin{equation*}
L = \int_1^4 \sqrt{1+\left(\frac{3}{2}x^{1/2}\right)^2}\ dx = \int_1^4 \sqrt{1+\frac{9}{4}x} \ dx
\end{equation*}
Para o integrando, fazemos a substituição $\displaystyle u = \frac{9}{4}x + 1$. Assim, $\displaystyle du = \frac{9}{4}dx$ e $\displaystyle dx = \frac{4}{9}du$.
Precisamos calcular os novos limites de integração para a variável $u$.
Para o limite inferior, substituímos $x$ por $1$:
\begin{equation*}
u=\frac{9}{4}x + 1 = \frac{9}{4}\cdot 1 + 1 = \frac{13}{4}
\end{equation*}
Para o limite superior, substituímos $x$ por $4$:
\begin{equation*}
u=\frac{9}{4}x + 1 = \frac{9}{4} \cdot 4 + 1 = 10
\end{equation*}
Assim:
\begin{equation*}
L = \frac{4}{9}\int_{13/4}^{10} \sqrt{u}\ du
\end{equation*}
A integral de $\displaystyle \sqrt{u}$ é $\displaystyle \frac{2u^{3/2}}{3}+C$. Assim:
\begin{equation*}
L = \frac{4}{9} \left[ \frac{2u^{3/2}}{3}\right]_{13/4}^{10}\\
\ \\
L=\frac{4}{9}\left[ \frac{2\cdot 10^{3/1}}{3} - \frac{\displaystyle 2\left(\frac{13}{4}\right)^{3/2}}{3} \right]\\
\ \\
L \approx 7,6337~~u.c.
\end{equation*}

A função $f(x)=\cosh (x)$ tem como derivada $f^{\prime} (x) = \text{senh}(x)$. Aplicando na relação $(5)$:
\begin{equation}
L = \int_{-e}^{e} \sqrt{1+\text{senh}^2(x)} \ dx
\end{equation}
Pela identidade fundamental trigonométrica hiperbólica, temos que:
\begin{equation}
\cosh^2 (x) - \text{senh}^2(x) = 1
\end{equation}
Substituinfo $(8)$ em $(7)$, obtemos:
\begin{equation*}
L = 2 \int_0^e \sqrt{\cosh ^2(x)}\ dx = 2 \int_0^e \cosh (x)\ dx\\
\ \\
L = \left[ 2\ \text{senh}(x) \right]_0^e = 2\ \text{senh}(e) \approx 15,088~~u.c.
\end{equation*}
Área em coordenadas polares
Método de Integração por substituição

- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a}\ Dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...
- Demonstração Da Derivada Da Função Produto
A derivada de uma função pode ser representada geometricamente da seguinte maneira: Se $\Delta x$ for tão pequeno quanto quisermos, a reta que passa pelos pontos $[(x,f(x)),(x+\Delta x, f(x+\Delta x))]$, se confunde com a reta tangente no ponto $x$...
Matemática
Como calcular o comprimento de um arco de curva

No século $XVII$, pouco antes da invenção do Cálculo Diferencial e Integral, existiam muitos métodos para os problemas de quadratura (cálculo de áreas), cubatura e retificação de uma curva.
O problema de calcular o comprimento de arco de uma curva é em alguns casos extremamente difícil, pois pode nos levar a integrais elípticas. Com a invenção do Cálculo Diferencial e Integral, este procedimento nos leva a resolução de uma integral definida em que o integrando envolve uma raiz quadrada e a derivada da função dada.
Para curvas geradas por funções do primeiro grau, basta aplicarmos o Teorema pitagórico no intervalo desejado que encontramos o comprimento da curva rapidamente.

O segmento $\ell$ é a hipotenusa do triângulo retângulo de catetos $\Delta x$ e $\Delta y$ e seu comprimento é dado por:
\begin{equation}
\ell = \sqrt{\Delta x^2 + \Delta y^2}
\end{equation}
Para as demais funções, temos que usar o Cálculo para determinarmos o comprimento desejado de um arco.
Considere a função $y=f(x)$, contínua no intervalo $[a,b]$ e derivável em $(a,b)$, cujo gráfico pode ser esboçado como:

Para determinarmos o comprimento do arco da curva entre os pontos $A=\left(a,f(a)\right)$ e $B=\left(b, f(b)\right)$, podemos subdividir a curva em segmentos infinitesimais de reta, que já sabemos calcular pela relação $(1)$, onde:
\begin{equation*}
x_0 = a < x_1 <x_2 < \cdots < x_{k-1} < x_k < \cdots < x_n = b
\end{equation*}
Conforme podemos observar na figura abaixo:

Seja $P_k$ o ponto $(x_k , y_k)$ onde $y_k = f(x_k)$. O comprimento total da poligonal $P_0P_1P_2\cdots P_{k-1}P_k\cdots P_n$ é a soma dos comprimentos das cordas que ligam cada ponto ao próximo.
Sejam $\Delta x_k = x_k - x_{k-1}$ e $\Delta y_k = y_k - y_{k-1}$ para $k=1,2,3, \cdots, n$.
Assim, temos triângulos retângulos e o problema se resumiria em encontrarmos os comprimentos infinitesimais de suas hipotenusas de tamanho $\ell_k$:

Pelo teorema pitagórico, o comprimento da k-ésima corda, denotada por $\ell _k$, é igual a:
\begin{equation*}
\ell_k = \sqrt{\left(\Delta x_k \right)^2 + \left(\Delta y_k \right)^2}\\
\ \\
\ell_k = \sqrt{\frac{\left(\Delta x_k \right)^2 + \left(\Delta y_k \right)^2}{\left(\Delta x_k \right)^2}\cdot \left(\Delta x_k \right)^2}\\
\ \\
\ell_k = \sqrt{1+\frac{\left(\Delta y_k \right)^2}{\left(\Delta x_k \right)^2}} \cdot \Delta x_k
\end{equation*}
\begin{equation}
\ell_k = \sqrt{1 + \left( \frac{\Delta y_k}{\Delta x_k}\right)^2} \Delta x_k
\end{equation}
Considerando $f(x)$ contínua no intervalo $[a,b]$ e derivável em $(a,b)$, então $f(x)$ é derivável no intervalo $[x_{k-1}, x_k]$ e pelo teorema do valor médio, existe $\xi_k \in (x_{k-1}, x_k)$, tal que:
\begin{equation}
\frac{\Delta y_k}{\Delta x_k} = f^{\prime} (\xi _k)
\end{equation}
Substituindo $(3)$ em $(2)$, temos que:
\begin{equation}
\ell _k = \sqrt{1+ \left[ f^{\prime} (\xi _k)\right]^2} \cdot \Delta x_k
\end{equation}
Mas, $\ell_k$ é somente o comprimento de um segmento infinitesimal da curva. Para o comprimento total da poligonal $L$, fazemos:
\begin{equation*}
L = \sum_{k=1}^n \ell_k = \sum_{k=1}^n \sqrt{1+\left[ f^{\prime} (\xi_k)\right]^2} \cdot \Delta x_k
\end{equation*}
Quando tende ao infinito, o comprimento do subintervalo tende a zero. Assim, se $L$ denota o comprimento do arco $AB$, então:
\begin{equation*}
L = \lim_{\max \Delta x_k \rightarrow 0} \sum_{k=1}^n \sqrt{1+ \left[ f^{\prime}(\xi _k)\right]^2} \cdot \Delta x_k
\end{equation*}
\begin{equation}
L = \int_a^b \sqrt{1+\left[ f^{\prime} (x) \right]^2} \ dx
\end{equation}
Isso com a hipótese adicional que $f^{\prime} (x)$ seja contínua para que a integral dada na relação $(5)$ exista.
Vejamos alguns exemplos para melhor ilustrar esta ideia.
Exemplo $1$
Seja a função $f(x)=2x-1$. Determinar o comprimento do arco da curva no intervalo $[1,2]$.Primeiramente calculamos a derivada da função:
\begin{equation*}
f(x) = 2x-1 \quad \Longrightarrow \quad f^{\prime}(x)=2
\end{equation*}
Em seguida, substituímos na fórmula $(5)$ para o comprimento do arco:
\begin{equation*}
L=\int_1^2 \sqrt{1+(2)^2}\ dx = \int_1^2 \sqrt{5}\ dx = \left[\sqrt{5} x\right]_1^2=\sqrt{5}~~u.c.
\end{equation*}
Graficamente temos:

Se utilizarmos o teorema pitagórico, obteríamos:
\begin{equation*}
L^2 = (3-1)^2 +(2-1)^2 \\
L=\sqrt{5}~~u.c.
\end{equation*}
Que é exatamente o que encontramos utilizando o cálculo diferencial e integral.
Podemos aplicar este conceito para diversas curvas mais complexas, mas dependendo da função original, podemos obter uma integral com bastante dificuldade de resolução. Vejamos outro exemplo:
Exemplo $2$
Seja a função $f(x) = x^{3/2}$. Determinar o comprimento da curva no intervalo $[1,4]$.
A função $f(x)=x^{3/2}$ tem como derivada $f^{\prime}(x)= \frac{3}{2}x^{1/2}$. Aplicamos a fórmula dada em $(5)$:
\begin{equation*}
L = \int_1^4 \sqrt{1+\left(\frac{3}{2}x^{1/2}\right)^2}\ dx = \int_1^4 \sqrt{1+\frac{9}{4}x} \ dx
\end{equation*}
Para o integrando, fazemos a substituição $\displaystyle u = \frac{9}{4}x + 1$. Assim, $\displaystyle du = \frac{9}{4}dx$ e $\displaystyle dx = \frac{4}{9}du$.
Precisamos calcular os novos limites de integração para a variável $u$.
Para o limite inferior, substituímos $x$ por $1$:
\begin{equation*}
u=\frac{9}{4}x + 1 = \frac{9}{4}\cdot 1 + 1 = \frac{13}{4}
\end{equation*}
Para o limite superior, substituímos $x$ por $4$:
\begin{equation*}
u=\frac{9}{4}x + 1 = \frac{9}{4} \cdot 4 + 1 = 10
\end{equation*}
Assim:
\begin{equation*}
L = \frac{4}{9}\int_{13/4}^{10} \sqrt{u}\ du
\end{equation*}
A integral de $\displaystyle \sqrt{u}$ é $\displaystyle \frac{2u^{3/2}}{3}+C$. Assim:
\begin{equation*}
L = \frac{4}{9} \left[ \frac{2u^{3/2}}{3}\right]_{13/4}^{10}\\
\ \\
L=\frac{4}{9}\left[ \frac{2\cdot 10^{3/1}}{3} - \frac{\displaystyle 2\left(\frac{13}{4}\right)^{3/2}}{3} \right]\\
\ \\
L \approx 7,6337~~u.c.
\end{equation*}
Exemplo $3$
Seja a função $f(x)=\cosh (x)$. Determinar o comprimento do arco da curva no intervalo $[e,-e]$.
A função $f(x)=\cosh (x)$ tem como derivada $f^{\prime} (x) = \text{senh}(x)$. Aplicando na relação $(5)$:
\begin{equation}
L = \int_{-e}^{e} \sqrt{1+\text{senh}^2(x)} \ dx
\end{equation}
Pela identidade fundamental trigonométrica hiperbólica, temos que:
\begin{equation}
\cosh^2 (x) - \text{senh}^2(x) = 1
\end{equation}
Substituinfo $(8)$ em $(7)$, obtemos:
\begin{equation*}
L = 2 \int_0^e \sqrt{\cosh ^2(x)}\ dx = 2 \int_0^e \cosh (x)\ dx\\
\ \\
L = \left[ 2\ \text{senh}(x) \right]_0^e = 2\ \text{senh}(e) \approx 15,088~~u.c.
\end{equation*}
Referências
[1] Cálculo com Geometria Analítica V1 - Simmons - Ed. McGraw Hill, São Paulo, 1987Veja mais
O Cálculo IntegralÁrea em coordenadas polares
Método de Integração por substituição

- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a}\ Dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...
- Demonstração Da Derivada Da Função Produto
A derivada de uma função pode ser representada geometricamente da seguinte maneira: Se $\Delta x$ for tão pequeno quanto quisermos, a reta que passa pelos pontos $[(x,f(x)),(x+\Delta x, f(x+\Delta x))]$, se confunde com a reta tangente no ponto $x$...
