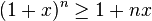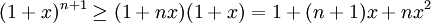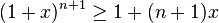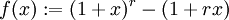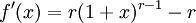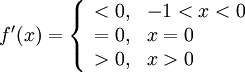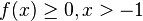Matemática

Em matemática, a desigualdade de Bernoulli afirma que:
Esta desigualdade pode ser generalizada substituindo n por r um real maior ou igual a 1.
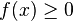 quando x > ? 1.
quando x > ? 1.
Tomando derivada em x, temos:
REFERÊNCIAS
http://pt.wikipedia.org/wiki/Desigualdade_de_Bernoulli
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- O Algoritmo Da Divisão Parte Ii
Nesta série de postagens estamos nos dedicando a demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
- A Desigualdade De Ptolomeu
Cláudio Ptolomeu foi um grande astrônomo e geômetra grego que viveu no século $I\ \text{d.C.}$. Neste post, provaremos uma desigualdade geométrica muito interessante. Proposição 1Dado o quadrilátero $ABCD$, onde $AC$ e $BD$ são as diagonais,...
- Valor Absoluto E A Desigualdade Triangular
Na reta real, podemos representar geometricamente um número real como um ponto. Convencionando que a reta é crescente da esquerda para a direita, podemos representar dois números arbitrários quaisquer: Temos representado os números a e b tal...
- Teste Da Integral Para Convergência De Séries
O teorema conhecido como teste da integral (ou teste de Leibniz) para verificar convergências de séries, faz uso da teoria de integrais impróprias. Teorema $1$:Se $f(n)$ representa o termo geral $u_n$ de uma série numérica infinita de termos positivos,...
Matemática
Desigualdade de Bernoulli

Em matemática, a desigualdade de Bernoulli afirma que:
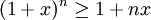
- sempre que x > ? 1 e n um número inteiro não negativo.
Esta desigualdade pode ser generalizada substituindo n por r um real maior ou igual a 1.
Demostração
Esta desigualdade pode ser provada por indução matemática, como se segue:- Base:
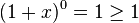 .
.
- Indução:
Demonstração da Versão mais Geral
Defina a função auxiliar f(x) por: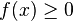 quando x > ? 1.
quando x > ? 1.Tomando derivada em x, temos:
REFERÊNCIAS
http://pt.wikipedia.org/wiki/Desigualdade_de_Bernoulli
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- O Algoritmo Da Divisão Parte Ii
Nesta série de postagens estamos nos dedicando a demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
- A Desigualdade De Ptolomeu
Cláudio Ptolomeu foi um grande astrônomo e geômetra grego que viveu no século $I\ \text{d.C.}$. Neste post, provaremos uma desigualdade geométrica muito interessante. Proposição 1Dado o quadrilátero $ABCD$, onde $AC$ e $BD$ são as diagonais,...
- Valor Absoluto E A Desigualdade Triangular
Na reta real, podemos representar geometricamente um número real como um ponto. Convencionando que a reta é crescente da esquerda para a direita, podemos representar dois números arbitrários quaisquer: Temos representado os números a e b tal...
- Teste Da Integral Para Convergência De Séries
O teorema conhecido como teste da integral (ou teste de Leibniz) para verificar convergências de séries, faz uso da teoria de integrais impróprias. Teorema $1$:Se $f(n)$ representa o termo geral $u_n$ de uma série numérica infinita de termos positivos,...