Matemática
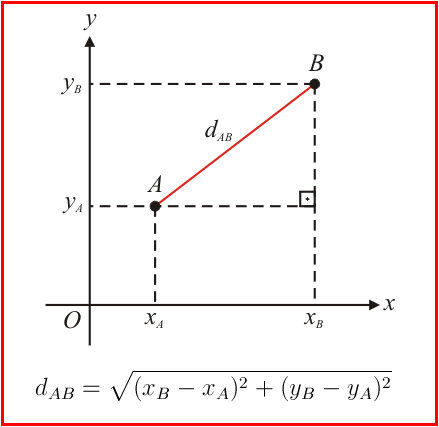No plano, dado dois ponto, o segmento formado por eles pode ser paralelo ao eixo dos $x$ ou ao eixo dos $y$, ou mesmo oblíquo a eles.
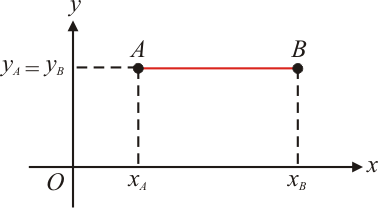Neste caso, as ordenadas dos pontos $A$ e $B$ são iguais, ou seja, $y_A=y_B$. A distância entre os pontos $A$ e $B$, ou o comprimento do segmento $\overline{AB}$, é dada pelo módulo da diferença entre as abscissas de $A$ e $B$, de modo que:
\begin{equation}
d_{AB}=\mid x_A-x_B \mid
\end{equation}
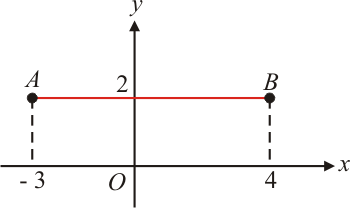
Exemplo $1$: Determinar a distância entre os pontos $A(-3,2)$ e $B(4,2)$.
\begin{aligned}
d_{AB}=\mid x_A-x_B \mid=\mid -3-4\mid=\mid -7\mid=7
\end{aligned}
d_{AB}=\mid y_A-y_B \mid
\end{equation}
\begin{aligned}
d_{AB}=\mid y_A-y_B \mid=\mid -2-3\mid=\mid -5\mid=5
\end{aligned}
\overline{AB}^2=\overline{AC}^2+\overline{BC}^2
\end{equation}
\overline{AB}^2=\mid x_A-x_B\mid ^2+\mid y_A-y_B\mid ^2
\end{equation}
(d_{AB})^2=(x_A-x_B)^2+(y_A-y_B)^2
\end{aligned}
Agora, basta extrairmos as raízes de ambos os lados da equação acima:
\begin{equation}
d_{AB}=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}
\end{equation}
d_{AB}=\sqrt{(\Delta x)^2+(\Delta y)^2}
\end{equation}
Exemplo $3$: Determine a distância entre os pontos $A(1,-1)$ e $B(4,-5)$.
\begin{aligned}
d_{AB}=\sqrt{(1-4)^2+(-1-(-5))^2}=\sqrt{(-3)^2+(4)^2}=\sqrt{9+16}=\sqrt{25}=5
\end{aligned}
d_{AB}=\sqrt{(2+4)^2+(2+6)^2}=\sqrt{36+64}=\sqrt{100}=10\\
d_{BC}=\sqrt{(-4-4)^2+(-6+12)^2}=\sqrt{64+36}=\sqrt{100}=10\\
d_{AC}=\sqrt{(2-4)^2+(2+12)^2}=\sqrt{4+196}=\sqrt{200}=10\sqrt{2}\\
\end{matrix}
(d_{AC})^2=(d_{AB})^2+(d_{BC})^2\\
(10\sqrt{2})^2=10^2+10^2\\
200=100+100
\end{matrix}
P=d_{AB}+d_{BC}+d_{AC}=10+10+10\sqrt{2}=10(2+\sqrt{2})
\end{aligned}
d_{AP}=\sqrt{(x_A-x_P)^2+(y_A-y_P)^2}=\sqrt{(2-x_P)^2+(4-0)^2}=\sqrt{(2-x_P)^2+16}\\
d_{BP}=\sqrt{x_B-x_P)^2+(y_B-y_P)^2}=\sqrt{(7-x_P)^2+(3-0)^2}=\sqrt{(7-x_P)^2+9}
\end{matrix}
Fazendo $d_{AP}=d_{BP}$, vem que:
\begin{matrix}
\sqrt{(2-x_P)^2+16}=\sqrt{(7-x_P)+9}\\
(2-x_P)^2+16=(7-x_P)^2+9\\
4-4x_P+x_P^2+16=49-14x_P+x_P^2+9\\
x_P=\frac{38}{10}=\frac{19}{5}=3 \frac{4}{5}
\end{matrix}Logo, $\displaystyle P \left ( \frac{19}{5},0\right )$.
Veja mais:
Retas Perpendiculares
Reta Tangente a uma Curva
Distância entre Dois Pontos na Superfície Terrestre no blog Fatos Matemáticos
- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...
- Distância De Um Ponto A Uma Reta
Veremos nesta postagem como determinar a fórmula para calcular a distância entre um ponto e uma reta. Seja $P$ um ponto qualquer e seja $r$ uma reta dada. A distância entre o ponto $P$ e a reta $r$ é a distância entre $P$ e sua projeção ortogonal...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...
Matemática
Distância Entre Dois Pontos No Plano
Nesta postagem, veremos como determinar a distância entre dois pontos distintos no plano cartesiano.
Definição: Sejam dois pontos distintos $A(x_A,y_A)$ e $B(x_B,y_B)$ no plano cartesiano. Distância é a medida do segmento de reta que tem os pontos $A$ e $B$ como extremidades.
$1^{\circ}$ caso: O segmento $\overline{AB}$ é paralelo ao eixo dos $x$
\begin{equation}
d_{AB}=\mid x_A-x_B \mid
\end{equation}
Exemplo $1$: Determinar a distância entre os pontos $A(-3,2)$ e $B(4,2)$.
\begin{aligned}
d_{AB}=\mid x_A-x_B \mid=\mid -3-4\mid=\mid -7\mid=7
\end{aligned}
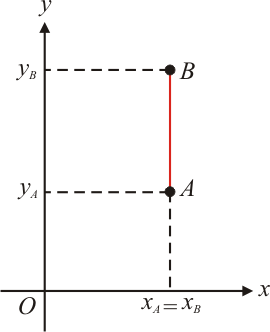
$2^{\circ}$ caso: O segmento $\overline{AB}$ é paralelo ao eixo dos $y$
Neste caso, as abscissas dos pontos $A$ e $B$ são iguais, ou seja, $x_A=x_B$. A distância entre os pontos $A$ e $B$, ou o comprimento do segmento $\overline{AB}$, é dada pelo módulo da diferença das ordenadas de $A$ e $B$, de modo que:
\begin{equation}d_{AB}=\mid y_A-y_B \mid
\end{equation}
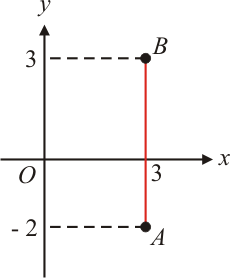
Exemplo $2$: Determinar a distância entre os pontos $A(3,-2)$ e $B(3,3)$.
\begin{aligned}
d_{AB}=\mid y_A-y_B \mid=\mid -2-3\mid=\mid -5\mid=5
\end{aligned}
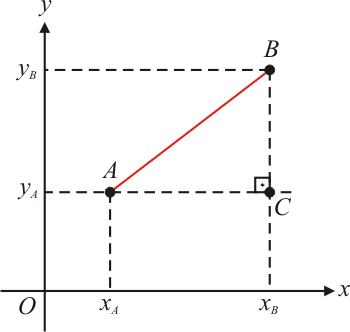
$3^{\circ}$ caso: O segmento $\overline{AB}$ é oblíquo aos eixos
Este é o caso geral, pois a fórmula que encontraremos também resolve os dois casos anteriores. Vejam que as retas que passam pelo ponto $x_B$ paralela ao eixo dos $y$ e pelo ponto $y_A$ paralela ao eixo dos $x$, definem um triângulo retângulo com hipotenusa $\overline{AB}$. Aplicando o Teorema de Pitágoras no triângulo $ABC$, obtemos:
\begin{equation}\overline{AB}^2=\overline{AC}^2+\overline{BC}^2
\end{equation}
No entanto, temos que $\overline{BC}=\mid y_A-y_B\mid$ e $\overline{AC}=\mid x_A-x_B\mid$. Se substituirmos em $(3)$, vem que:
\begin{equation}\overline{AB}^2=\mid x_A-x_B\mid ^2+\mid y_A-y_B\mid ^2
\end{equation}
Como para todo $a \in \mathbb {R}$, então $\mid a \mid ^2=a^2$, reescrevemos a equação $(4)$:
\begin{aligned}(d_{AB})^2=(x_A-x_B)^2+(y_A-y_B)^2
\end{aligned}
Agora, basta extrairmos as raízes de ambos os lados da equação acima:
\begin{equation}
d_{AB}=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}
\end{equation}
Vejam ainda que $(x_A-x_B)^2=(x_B-x_A)^2$ do mesmo modo que $(y_A-y_B)^2=(y_B-y_A)^2$. Assim, ainda podemos reescrever a equação $(5)$ como:
\begin{equation}d_{AB}=\sqrt{(\Delta x)^2+(\Delta y)^2}
\end{equation}
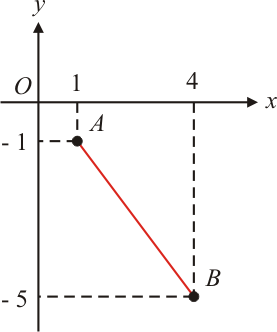
Exemplo $3$: Determine a distância entre os pontos $A(1,-1)$ e $B(4,-5)$.
\begin{aligned}
d_{AB}=\sqrt{(1-4)^2+(-1-(-5))^2}=\sqrt{(-3)^2+(4)^2}=\sqrt{9+16}=\sqrt{25}=5
\end{aligned}
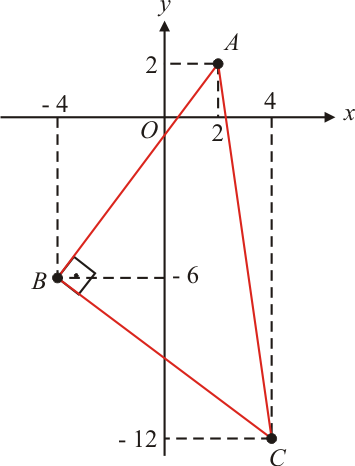
Exemplo $4$: Mostrar que os pontos $A(2,2)$, $B(-4,-6)$ e $C(4,-12)$ formam um triângulo retângulo e isósceles e calcule seu perímetro.
Primeiramente vamos calcular as medidas dos lados do triângulo $ABC$ e ver se formam uma terna pitagórica.
\begin{matrix}d_{AB}=\sqrt{(2+4)^2+(2+6)^2}=\sqrt{36+64}=\sqrt{100}=10\\
d_{BC}=\sqrt{(-4-4)^2+(-6+12)^2}=\sqrt{64+36}=\sqrt{100}=10\\
d_{AC}=\sqrt{(2-4)^2+(2+12)^2}=\sqrt{4+196}=\sqrt{200}=10\sqrt{2}\\
\end{matrix}
Agora, aplicamos os valores encontrados acima no Teorema de Pitágoras e verificamos se o satisfaz. Como a maior distância é do segmento $\overline{AC}=10\sqrt{2}$, concluímos que a hipotenusa é o segmento $\overline{AC}$.
\begin{matrix}(d_{AC})^2=(d_{AB})^2+(d_{BC})^2\\
(10\sqrt{2})^2=10^2+10^2\\
200=100+100
\end{matrix}
Logo, o triângulo $ABC$ é retângulo e é isósceles, pois ambos os catetos são iguais. O perímetro do triângulo é dado pela soma dos lados:
\begin{aligned}P=d_{AB}+d_{BC}+d_{AC}=10+10+10\sqrt{2}=10(2+\sqrt{2})
\end{aligned}
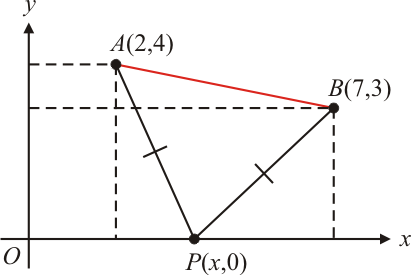
Exemplo $5$: Dados os pontos $A(2,4)$ e $B(7,3)$, determinar o ponto $P$ sobre o eixo dos $x$ de modo que seja equidistante a $A$ e a $B$.
Como o ponto $P \in Ox \Rightarrow P(x,0)$ e como $P$ é equidistante a $A$ e $B$, então $d_{AP}=d_{BP}$. Então:
\begin{matrix}d_{AP}=\sqrt{(x_A-x_P)^2+(y_A-y_P)^2}=\sqrt{(2-x_P)^2+(4-0)^2}=\sqrt{(2-x_P)^2+16}\\
d_{BP}=\sqrt{x_B-x_P)^2+(y_B-y_P)^2}=\sqrt{(7-x_P)^2+(3-0)^2}=\sqrt{(7-x_P)^2+9}
\end{matrix}
Fazendo $d_{AP}=d_{BP}$, vem que:
\begin{matrix}
\sqrt{(2-x_P)^2+16}=\sqrt{(7-x_P)+9}\\
(2-x_P)^2+16=(7-x_P)^2+9\\
4-4x_P+x_P^2+16=49-14x_P+x_P^2+9\\
x_P=\frac{38}{10}=\frac{19}{5}=3 \frac{4}{5}
\end{matrix}Logo, $\displaystyle P \left ( \frac{19}{5},0\right )$.
Veja mais:
Retas Perpendiculares
Reta Tangente a uma Curva
Distância entre Dois Pontos na Superfície Terrestre no blog Fatos Matemáticos
- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...
- Distância De Um Ponto A Uma Reta
Veremos nesta postagem como determinar a fórmula para calcular a distância entre um ponto e uma reta. Seja $P$ um ponto qualquer e seja $r$ uma reta dada. A distância entre o ponto $P$ e a reta $r$ é a distância entre $P$ e sua projeção ortogonal...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...