Matemática
Construção Geométrica
Equação das Bissetrizes
d_{Pr}=d_{Ps}
\end{equation}
d_{PP'}=\frac{\mid ax + by +c \mid}{\sqrt{a^2+b^2}}
\end{equation}
Assim temos que:
\begin{equation}
\left\{
\begin{matrix}
d_{Pr}=\frac{\mid a_1x+b_1y+c_1=0\mid}{\sqrt{a_1^2+b_1^2}}\\
d_{Ps}=\frac{\mid a_2x+b_2y+c_2=0\mid}{\sqrt{a_2^2+b_2^2}}\end{matrix}
\right.
\end{equation}
E pela equação dada em $(1)$:
\begin{equation}
\frac{\mid a_1x+b_1y+c_1=0\mid}{\sqrt{a_1^2+b_1^2}}=\frac{\mid a_2x+b_2y+c_2=0\mid}{\sqrt{a_2^2+b_2^2}}
\end{equation}
\frac{ a_1x+b_1y+c_1=0}{\sqrt{a_1^2+b_1^2}}=\pm \frac{a_2x+b_2y+c_2=0}{\sqrt{a_2^2+b_2^2}}
\end{equation}
\alpha+\beta=\alpha+\frac{1}{2}(180°-2\alpha)=\alpha+90°-\alpha=90°
\end{equation}
\begin{matrix}
4\alpha + 4\beta=360°\\
4(\alpha+\beta)=360°\\
\alpha + \beta=90°
\end{matrix}
\end{equation}
Aplicando a fórmula das bissetrizes dada em $(5)$, temos:
$$\frac{ a_1x+b_1y+c_1=0}{\sqrt{a_1^2+b_1^2}}=\pm \frac{a_2x+b_2y+c_2=0}{\sqrt{a_2^2+b_2^2}}$$
$$\frac{ 3x+2y-7=0}{\sqrt{3^2+2^2}}=\pm \frac{2x-3y+1=0}{\sqrt{2^2+(-3)^2}}$$
$$\frac{ 3x+2y-7=0}{\sqrt{13}}=\pm \frac{2x-3y+1=0}{\sqrt{13}}$$
$$3x+2y-7=\pm 2x-3y+1$$
$$b_1: 3x+2y-7=2x-3y+1 \Rightarrow x+5y-8=0$$
$$b_2: 3x+2y-7=-2x+3y-1 \Rightarrow 5x-y-6=0$$
Os coeficientes angulares de $b_1$ e $b_2$ são dados respectivamente por:
$$m_1=-\frac{a_1}{b_1} \qquad \text{e} \qquad m_2=-\frac{a_2}{b_2}$$
Assim:
$$m_1\cdot m_2=-\frac{1}{5}\cdot 5=-1$$
Comprovando a perpendicularidade entre as bissetrizes.
Exemplo $2$: Sejam as retas $r: x-3y+5=0$ e $s: 6x-2y-3=0$. Obter as equações das bissetrizes.
Aplicando a fórmula das bissetrizes, obtemos:
$$\frac{ a_1x+b_1y+c_1=0}{\sqrt{a_1^2+b_1^2}}=\pm \frac{a_2x+b_2y+c_2=0}{\sqrt{a_2^2+b_2^2}}$$
$$\frac{ x-3y+5=0}{\sqrt{1^2+(-3)^2}}=\pm \frac{6x-2y-3=0}{\sqrt{6^2+(-2)^2}}$$
$$\frac{x-3y+5=0}{\sqrt{10}}=\pm \frac{6x-2y-3=0}{2\sqrt{10}}$$
$$\frac{2(x-3y+5=0)}{\sqrt{10}}=\pm \frac{6x-2y-3=0}{\sqrt{10}}$$
$$2x-6y+10=\pm 6x-2y-3$$
$$b_1: 2x-6y+10=6x-2y-3 \Rightarrow 4x+4y-13=0$$
$$b_2: 2x-6y+10=-6x+2y+3 \Rightarrow 8x-8y+7=0$$
Para comprovar a perpendicularidade entre as bissetrizes, fazemos:
$$m_1=-\frac{a_1}{b_1}=-\frac{4}{4}=-1 \qquad \text{e} \qquad m_2=-\frac{a_2}{b_2}=\frac{8}{8}=1$$
Assim:
$$m_1\cdot m_2=-1 \cdot 1=-1$$
Veja mais:
Distância de um Ponto a uma Reta
Distância entre Dois Pontos no Plano
Teorema da Bissetriz Interna
Teorema da Bissetriz Interna Através da Leis dos Senos no blog Fatos Matemáticos

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a}\ Dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
- Ângulo De Segmento Ou ângulo Semi-inscrito
Nesta postagem, veremos como determinar o ângulo de segmento e provar que vale a metade do ângulo central. Definição:Ângulo de segmento ou ângulo semi-inscrito relativo a uma circunferência é o ângulo que tem o vértice num ponto da circunferência,...
Matemática
Equação das Bissetrizes dos Ângulos Formados por Duas Retas Concorrentes
Nesta postagem veremos como construir a bissetriz de um ângulo dado utilizando apenas régua e compasso e também como obter a equação das bissetrizes dos ângulos formado por duas retas concorrentes fazendo uso da Geometria Analítica.
[Figura 1]
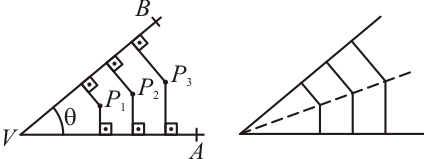
Primeiramente, vamos considerar um ângulo $A\hat{V} B$. É verdade que existe um ponto interno que é equidistante aos lados deste ângulo. Na verdade, existem infinitos pontos.
[Figura 2]
A reunião desses infinitos pontos, sendo esses equidistantes aos lados do ângulo, geram uma semirreta notável denominada bissetriz, dividindo o ângulo $A \hat{V} B$ em dois ângulos iguais.
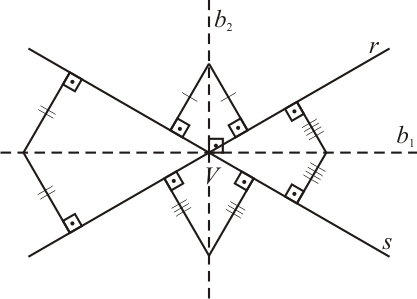
Ampliando esta ideia, vamos considerar as retas $r$ e $s$ concorrentes no ponto $V$. Ao invés de um ângulo, teremos quatro ângulos e para cada um deles teremos pontos equidistantes aos respectivos lados e a reunião desses pontos constitui as bissetrizes dos ângulos. Essas bissetrizes formam duas novas retas $b_1$ e $b_2$, perpendiculares entre si.
[Figura 3]
Definição: O lugar geométrico dos pontos equidistantes de duas retas concorrentes $r$ e $s$, constitui um par de retas perpendiculares, as quais contém as bissetrizes dos ângulos determinados pelas retas $r$ e $s$.
Construção Geométrica
Seja dado um ângulo arbitrário de vértice $V$. Para construirmos a bissetriz do ângulo, procedemos como se segue.
$1)$ Descreva um arco de circunferência de raio $r$ centrado em $V$, interceptando os lados do ângulo nos pontos $A$ e $B$;
$2)$ Com centro em $A$, e depois em $B$, descreva dois arcos de circunferência de mesmo raio que se interceptam num ponto $P$;
$3)$ A bissetriz é a semirreta de origem em $V$ que passa pelo ponto $P$.
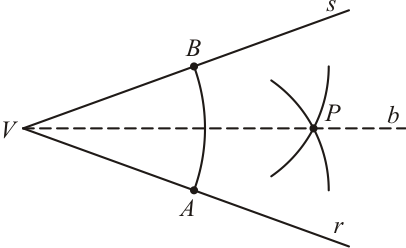

[Figura 4]
Equação das Bissetrizes
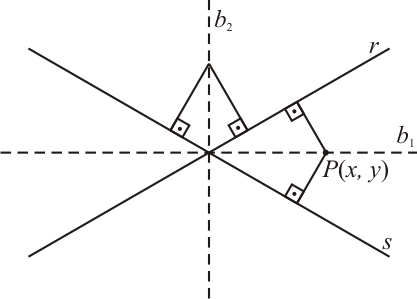
Sejam duas retas concorrentes definidas como $r: a_1x+b_1y+c_1=0$ e $s:a_2x+b_2y+c_2=0$, que se interceptam em um ponto $V$. Se $P(x,y)$ é um ponto genérico de uma bissetriz, sendo $P\neq V$, então $P$ equidista das retas $r$ e $s$.
\begin{equation}d_{Pr}=d_{Ps}
\end{equation}
Já vimos que a fórmula da distância de um ponto a uma reta é dada por:
\begin{equation}d_{PP'}=\frac{\mid ax + by +c \mid}{\sqrt{a^2+b^2}}
\end{equation}
Assim temos que:
\begin{equation}
\left\{
\begin{matrix}
d_{Pr}=\frac{\mid a_1x+b_1y+c_1=0\mid}{\sqrt{a_1^2+b_1^2}}\\
d_{Ps}=\frac{\mid a_2x+b_2y+c_2=0\mid}{\sqrt{a_2^2+b_2^2}}\end{matrix}
\right.
\end{equation}
E pela equação dada em $(1)$:
\begin{equation}
\frac{\mid a_1x+b_1y+c_1=0\mid}{\sqrt{a_1^2+b_1^2}}=\frac{\mid a_2x+b_2y+c_2=0\mid}{\sqrt{a_2^2+b_2^2}}
\end{equation}
Os denominadores não podem ser negativos, de modo que se existir alguma razão negativa será devido ao módulo nos numeradores. Se temos $\mid x\mid=\mid y\mid$, então $x=\pm y$. logo, podemos reescrever a equação $(4)$ como:
\begin{equation}\frac{ a_1x+b_1y+c_1=0}{\sqrt{a_1^2+b_1^2}}=\pm \frac{a_2x+b_2y+c_2=0}{\sqrt{a_2^2+b_2^2}}
\end{equation}
Vejam que o sinal de $\pm$ na equação $(5)$ permite dois resultados distintos, o que remete a duas bissetrizes. Isso é perfeitamente explicável pelo fato de que, dadas as retas concorrentes $r$ e $s$, estas formarão dois pares de ângulos opostos pelo vértice e para cada par de ângulos, teremos uma bissetriz.
[Figura 5]
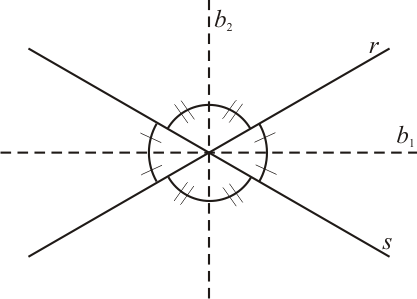
Uma propriedade importante das bissetrizes dos ângulos formados por duas retas concorrentes é que sempre serão perpendiculares entre si. Esta é a condição de existência das bissetrizes.
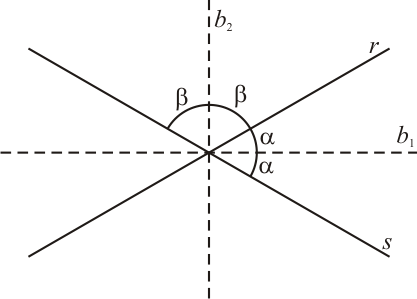
Sejam duas retas concorrentes $r$ e $s$ não perpendiculares entre si. Sejam $2 \alpha$ o ângulo agudo entre as retas $r$ e $s$ e seja $2 \beta$ o ângulo obtuso dado por $2\beta = 180°-2\alpha$.
[Figura 6]
Queremos provar que $\alpha + \beta = 90°$. Vejam que $2 \beta=180°-2\alpha$ e $\displaystyle \beta = \frac{1}{2}(180°-2\alpha)$. Assim:
\begin{equation}\alpha+\beta=\alpha+\frac{1}{2}(180°-2\alpha)=\alpha+90°-\alpha=90°
\end{equation}
Outra forma de demonstrar a perpendicularidade entre as bissetrizes é que, considerando a imagem acima, temos a relação:
\begin{equation}\begin{matrix}
4\alpha + 4\beta=360°\\
4(\alpha+\beta)=360°\\
\alpha + \beta=90°
\end{matrix}
\end{equation}
Exemplo $1$: Sejam as retas $r:3x+2y-7=0$ e $s:2x-3y+1=0$. Determinar as equações de suas bissetrizes.
Aplicando a fórmula das bissetrizes dada em $(5)$, temos:
$$\frac{ a_1x+b_1y+c_1=0}{\sqrt{a_1^2+b_1^2}}=\pm \frac{a_2x+b_2y+c_2=0}{\sqrt{a_2^2+b_2^2}}$$
$$\frac{ 3x+2y-7=0}{\sqrt{3^2+2^2}}=\pm \frac{2x-3y+1=0}{\sqrt{2^2+(-3)^2}}$$
$$\frac{ 3x+2y-7=0}{\sqrt{13}}=\pm \frac{2x-3y+1=0}{\sqrt{13}}$$
$$3x+2y-7=\pm 2x-3y+1$$
$$b_1: 3x+2y-7=2x-3y+1 \Rightarrow x+5y-8=0$$
$$b_2: 3x+2y-7=-2x+3y-1 \Rightarrow 5x-y-6=0$$
Pelo teorema das retas perpendiculares, duas retas serão perpendiculares entre si se o coeficiente angular de uma delas for igual ao oposto do inverso da outra:
$$m_1\cdot m_2=-1$$Os coeficientes angulares de $b_1$ e $b_2$ são dados respectivamente por:
$$m_1=-\frac{a_1}{b_1} \qquad \text{e} \qquad m_2=-\frac{a_2}{b_2}$$
Assim:
$$m_1\cdot m_2=-\frac{1}{5}\cdot 5=-1$$
Comprovando a perpendicularidade entre as bissetrizes.
Exemplo $2$: Sejam as retas $r: x-3y+5=0$ e $s: 6x-2y-3=0$. Obter as equações das bissetrizes.
Aplicando a fórmula das bissetrizes, obtemos:
$$\frac{ a_1x+b_1y+c_1=0}{\sqrt{a_1^2+b_1^2}}=\pm \frac{a_2x+b_2y+c_2=0}{\sqrt{a_2^2+b_2^2}}$$
$$\frac{ x-3y+5=0}{\sqrt{1^2+(-3)^2}}=\pm \frac{6x-2y-3=0}{\sqrt{6^2+(-2)^2}}$$
$$\frac{x-3y+5=0}{\sqrt{10}}=\pm \frac{6x-2y-3=0}{2\sqrt{10}}$$
$$\frac{2(x-3y+5=0)}{\sqrt{10}}=\pm \frac{6x-2y-3=0}{\sqrt{10}}$$
$$2x-6y+10=\pm 6x-2y-3$$
$$b_1: 2x-6y+10=6x-2y-3 \Rightarrow 4x+4y-13=0$$
$$b_2: 2x-6y+10=-6x+2y+3 \Rightarrow 8x-8y+7=0$$
Para comprovar a perpendicularidade entre as bissetrizes, fazemos:
$$m_1=-\frac{a_1}{b_1}=-\frac{4}{4}=-1 \qquad \text{e} \qquad m_2=-\frac{a_2}{b_2}=\frac{8}{8}=1$$
Assim:
$$m_1\cdot m_2=-1 \cdot 1=-1$$
Veja mais:
Distância de um Ponto a uma Reta
Distância entre Dois Pontos no Plano
Teorema da Bissetriz Interna
Teorema da Bissetriz Interna Através da Leis dos Senos no blog Fatos Matemáticos

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a}\ Dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
- Ângulo De Segmento Ou ângulo Semi-inscrito
Nesta postagem, veremos como determinar o ângulo de segmento e provar que vale a metade do ângulo central. Definição:Ângulo de segmento ou ângulo semi-inscrito relativo a uma circunferência é o ângulo que tem o vértice num ponto da circunferência,...
