Matemática

Lobachevsky e as Geometrias Não-Euclidianas

Tudo começou com Euclides, cerca de $300a.C.$, em sua obra-prima Os Elementos a geometria foi construída sobre cinco postulados:

$I-$ Fique postulado traçar uma reta a partir de todo ponto até todo ponto.
$II-$ Também prolongar uma reta limitada, continuamente, sobre uma reta.
$III-$ E, com todo centro e distância, descrever um círculo.
$IV-$ E serem iguais entre si todos os ângulos retos.
$V-$ E, caso uma reta, caindo sobre duas retas, faça ângulos interiores e do mesmo lado menores que dois retos, sendo prolongados as duas retas, ilimitadamente, encontram-se no lado no qual estão os menores do que dois retos.

Este quinto postulado em especial, certamente não traduzia nenhuma experiência concreta. Além disso Euclides só o enunciou depois de provar o máximo possível de teoremas sem usá-lo. Hoje podemos escrevê-lo assim:

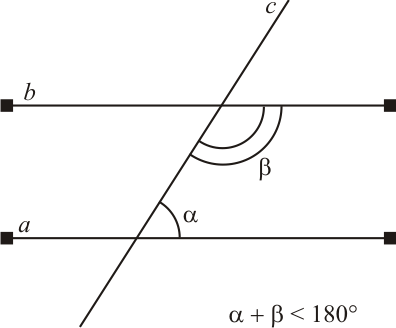
Postulado $V$: Se num plano duas retas $a$ e $b$ são interceptadas por uma transversal $c$ de modo a formar um par de ângulos colaterais internos de soma menor que $180°$, então essas retas, prolongadas indefinidamente, se cortam do lado em que estão os ângulos considerados.

Na verdade Euclides trabalhava, em sua geometria, como em particular no postulado $V$, com segmentos de reta que prolongava num ou noutro sentido, conforme necessitasse, ao invés de retas infinitas acabadas, como se faz hoje. E o que esse postulado afirma equivale, na versão moderna da geometria euclidiana, a admitir que por um ponto fora de uma reta não há mais que uma paralela à reta. Entre as implicações importantes do postulado $V$ está o teorema que assegura ser a soma dos ângulos internos de um triângulo igual a um ângulo raso.

Desde os tempos de Euclides dezenas de matemáticos tentaram provar esse postulado, a partir dos outros quatro, achando que se tratasse na verdade de mais um teorema. Um deles foi Nikolai Ivanovich Lobachevsky $(1792-1856)$, um russo natural da atual cidade de Gorki, cuja vida acadêmica sempre esteve vinculada à Universidade de Kazan, desde seu ingresso como aluno de $1827$ a $1846$. Diga-se de passagem que o fato de Lobachevsky ter alcançado a reitoria da Universidade de Kazan não foi um prêmio a seus méritos científicos. Estes jamais foram reconhecidos devidamente durante sua vida. Pelo contrário, uma versão de suas ideias geométricas, datando de $1829-30$, chegou a ser recusada para publicação pela Academia de Ciências de São Petersburgo.

Na mesma época, o matemático húngaro János Bolyai $(1802-1860)$ anunciou, de forma independente, a descoberta de geometrias não-euclidianas. O trabalho de Lobachevsky é de $1829$ e o de Bolyai nasceu como um apêndice de um livro publicado por seu pai em $1831$.

Quando jovem, o pai de Boylai havia sido colega de Gauss $(1777-1855)$ em Göttingen, e quando o filho pôs suas ideias por escrito, seu pai enviou um exemplar do manuscrito a Gauss, que não se sensibilizou ao entusiasmo do jovem János, escrevendo de volta: "Sim, mas isso que seu filho fez não é novidade para mim, que percebi essa possibilidade há muitos anos, em minha juventude". Hoje sabemos que foi Gauss mesmo o primeiro matemático a perceber a possibilidade das geometrias não-euclidianas.

Lobachevsky e Bolyai começaram negando o postulado das paralelas e procedendo a deduzir uma série de teoremas bem diferentes dos conhecidos teoremas da antiga geometria euclidiana. Afirmaram, então, terem descoberto uma geometria alternativa à geometria euclidiana, isto é, uma geometria sem contradições internas e de resultados surpreendentes e que hoje são considerados descobridores dessa geometria conhecida hoje como Geometria Hiperbólica. Por exemplo, nessa geometria, a soma dos ângulos internos de um triângulo vale menos que $180°$.

Cabe então a pergunta: tamanha liberdade é válida em matemática? Não é difícil nos convencermos que sim. Primeiro notemos que a geometria considerada por Euclides ao chegar ao postulado $V$ referia-se a um plano. Ademais, o conceito de reta é primitivo: não se define, não poderia haver nesta algum ente que fizesse o papel análogo ao da reta no plano, perante o mesmo conjunto de postulados?

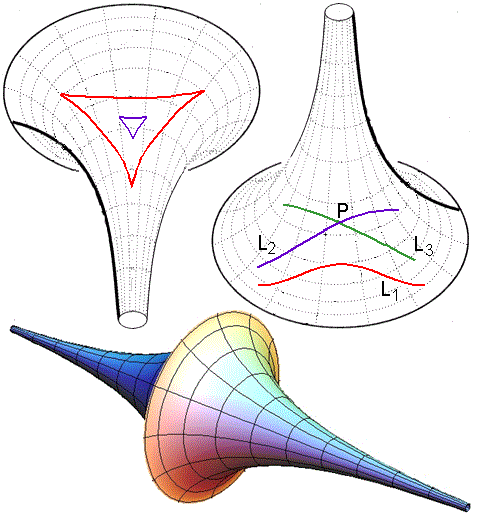
Tanto isso é possível que em $1868$ o matemático italiano Eugênio Beltrami $(1835-1900)$ descobriu um modelo para a geometria hiperbólica, a pseudo-esfera, superfície que lembra uma corneta dupla.

Nessa superfície, por um ponto fora de uma "reta" há mais do que uma paralela a essa "reta". Claro que a "reta" nesse caso indica o ente da pseudo-esfera cuja ideia corresponde à da reta de um plano. Na figura acima podemos visualizar como ocorre, bem como que a soma dos ângulos internos de um "triângulo" vale menos que um ângulo raso. A partir desse modelo, a geometria que o próprio Lobachevsky chamava de imaginária passou a ser matematicamente real.

As geometrias não-euclidianas, objeto das pesquisas de Lobachevsky, eram um verdadeiro tabu em sua época, daí a marginalização científica de que foi vítima o geômetra russo (agradava pelo fato de trabalhar num local muito distante dos grandes centros da Europa ocidental). Mas isso não impediu que se tornasse público que foi ele o primeiro a publicar um trabalho sobre geometrias não-euclidianas $(1826)$. E ganhou, assim, a primazia de ter acabado com o mito da verdade absoluta na matemática.

Referências:

[1] Fundamentos de Matemática Elementar V10 - Geometria Espacial, Posição e Métrica - Osvaldo Dolce & José Nicolau Pompeo
[2] Várias Faces da Matemática - Tópicos para Licenciatura e Leitura Geral - Geraldo Ávila
[3] Os Elementos de Euclides - Tradução e Introdução de Irineu Bicudo

Veja mais:

Gauss e o Universal em Matemática
Integração por Substituição Trigonométrica

- Tentativas De Demonstração Do Quinto Postulado De Euclides Do Século Iii A.c. Ao Século Xxi.
            Aproximadamente em 300 a. C., Euclides escreveu os Elementos. No século I a.C., Posidônio apresentou uma definição de paralelismo segundo a qual as retas paralelas...

- A Demonstração Do Quinto Postulado De Euclides Por Ptolomeu
          Ptolomeu, ou Claudius Ptolemaeus, foi geógrafo e astrônomo e viveu no século II, em Alexandria. Foi o autor de um famoso tratado de astronomia em 13 livros, que chegou até à...

- A Demonstração Do Quinto Postulado De Euclides - Postulado Das Paralelas
             Sabe-se muito pouco sobre Euclides. Sabe-se que nasceu depois dos discípulos diretos de Platão, mas antes de Erastóstenes e Arquimedes e que viveu em Alexandria...

- Solução: Como "construir Um Triângulo Equilátero Sobre A Reta Limitada Dada"?
[veja o problema] Consideremos a solução apresentada por Euclides: Seja a reta limitada dada AB. É preciso, então, sobre a reta AB construir um triângulo equilátero.Fique descrito, por um lado, com o centro A, e, por outro lado, com a distância...

- Como "construir Um Triângulo Equilátero Sobre A Reta Limitada Dada"?
Quando um estudante perguntou para que servia o estudo da geometria, Euclides disse a seu escravo que desse três moedas ao estudante, ?pois ele precisa ter lucro com o que aprende? (Boyer, p.69) Considere o seguinte problema: Construa, com régua e...

Matemática