Matemática

O Problema Inverso

Em Física é comum problemas em que conhecemos a velocidade instantânea $v(t)$ entre um da instante de tempo $t_a$ e um instante final $t_b$ e termos que descobrir o espaço percorrido. Este problema é chamado de problema inverso ao estudarmos movimento unidimensional.

Para o cálculo da velocidade instantânea $v(t)$ em um trajeto, basta conhecermos a lei horária $x=x(t)$, o que nos leva à notação:

\begin{equation}
v(t)=\frac{dx}{dt}
\end{equation}

que é o limite da variação do espaço percorrido num espaço de tempo infinitesimal:

\begin{equation}
v=\lim_{\Delta t \rightarrow 0} \left [\frac{x(t_0+\Delta t)-x(t_0)}{\Delta t} \right ]=\lim_{\Delta t \rightarrow 0}\left (\frac{\Delta x}{\Delta t}\right )=\frac{dx}{dt}
\end{equation}

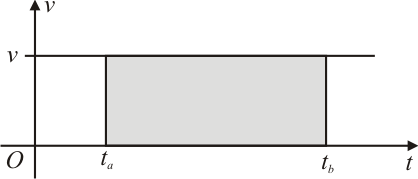
Se o movimento for uniforme, a velocidade instantânea se confunde com a velocidade média, sendo $v=\bar{v}=$constante, e podemos esboçar o gráfico como uma reta paralela ao eixo das abscissas:

Pela definição da velocidade média, temos que:

\begin{equation}
v=\bar{v}_{t_2 \rightarrow t_1}=\frac{\Delta x}{\Delta t}\Rightarrow
\Delta x=v\cdot \Delta t\Rightarrow
\Delta x=v(t_2-t_1)
\end{equation}

Vejam que o espaço percorrido equivalente à área do retângulo hachurado no gráfico $(v \times t)$ da imagem acima, compreendida entre a curva da velocidade que corta o eixo das ordenadas em $v$ e o eixo das abscissas limitadas pelos limites $t_a$ e $t_b$.

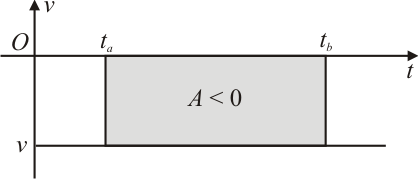
Podemos notar ainda que o retângulo pode aparecer sob o eixo das abscissas, que nos leva a um valor negativo para a área, o que significa simplesmente que $x(t_b) < x(t_1)$, correspondendo a um movimento para trás.

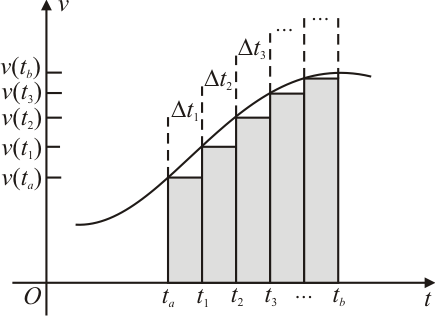
Para um movimento não-uniforme, em que $v$ é uma função qualquer de $t$, temos que analisar um pouco mais de perto. Num intervalo de tempo $[t_a,t_b]$, subdividimos em uma infinidade de intervalos de larguras $\Delta t_1$, $\Delta t_2$, $\Delta t_3$, $\cdots$, $\Delta t_i$, para $i=1,2,3,\cdots$ por pontos de divisão $t_1$, $t_2$, $t_3$, $\cdots$, $t_i$. Vejam que se tomarmos intervalos cada vez menores, haverá uma variação muito pequena da velocidade em cada um desses intervalos e a velocidade média se confunde com a velocidade instantânea, e assim podemos calcular a distância percorrida em cada intervalo:

\begin{matrix}
\bullet \Delta x_{{t_1}\rightarrow t_a}=x(t_1)-x(t_a)=\bar{v}_{{t_1}\rightarrow t_a}\cdot \Delta t_1\approx v(t_1) \Delta t_1\\
\bullet \Delta x_{{t_2}\rightarrow t_1}=x(t_2)-x(t_1)=\bar{v}_{{t_2}\rightarrow t_1}\cdot \Delta t_2\approx v(t_2) \Delta t_2\\
\bullet\Delta x_{{t_3}\rightarrow t_2}=x(t_3)-x(t_2)=\bar{v}_{{t_3}\rightarrow t_2}\cdot \Delta t_3\approx v(t_3) \Delta t_2\\
\end{matrix}

Somando membro a membro as relações acima, obtemos o deslocamento entre os espaços de tempo $t_a$ e $t_3$:

\begin{equation}
x(t_3)-x(t_a)\approx v(t_1)\Delta t_1+v(t_2)\Delta t_2+v(t_3)\Delta t_3
\end{equation}

Se o intervalo $[t_a,t_b]$ for subdividido em uma quantidade grande de intervalos, obtemos:

\begin{equation}
x(t_b)-x(t_a)=\sum_i v(t_i)\Delta t_i
\end{equation}

Se analisarmos a figura acima, cada retângulo equivale a um termo da soma $(5)$, que por sua vez corresponde à área entre o eixo das abscissas e a poligonal em "escada" inscrita na curva de $v$, no intervalo $[t_a,t_b]$.

A soma $(5)$ se aproxima melhor do resultado exato quanto menores forem as subdivisões $\Delta t_i$. Logo, no limite em que as subdivisões tendem a zero, obtemos:

\begin{equation}
x(t_b)-x(t_a)=\lim_{\Delta t_i \rightarrow 0} \sum_i v(t_i)\Delta t_i=\int_a^b v(t)dt
\end{equation}
que é a área entre a curva $(v \times t)$ e o eixo $Ot$ entre os limites $t_a$ e $t_b$.

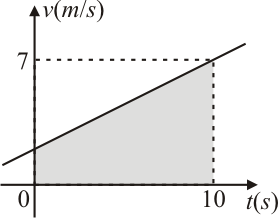
Exemplo: Considere um móvel que se desloca segundo a equação: $\displaystyle v(t)=\frac{1}{2}t+2$. Calcular o deslocamento efetuado durante o espaço de tempo de $0$ a $10$ segundos.

O deslocamento do móvel pode ser obtido calculando a área do trapézio, dada pela semi-soma das bases multiplicada pela altura do trapézio. Assim:

\begin{equation*}
\Delta x \approx \frac{1}{2}(v_1+v_2)(t_b-t_a)=\frac{1}{2}(2+7)(10-0)=\frac{90}{2}=45m
\end{equation*}
Podemos também verificar o resultado utilizando a integral dada em $(6)$:
\begin{matrix}
\Delta x=\int_a^b v(t)dt=\int_0^{10} \frac{1}{2}t+2 dt\\
=\left [\frac{1}{4}t^2+2t \right]_0^{10}=\frac{1}{4}\cdot 10^2+2\cdot 10=\frac{100}{4}+20=45m
\end{matrix}

Referências:
[1] Curso de Física Básica V1 - Moysés Nessenzveig

Veja mais:

Movimento Unidimensional
Equação Horária da Velocidade
Equação de Torricelli

- Os Pontos De Brocard (parte 3)
Vimos na primeira postagem desta série sobre os Pontos de Brocard as definições e suas construções geométricas. Na segunda postagem, vimos algumas propriedades importantes, teoremas e corolários. Nesta terceira parte, veremos outros teoremas igualmente...

- Usando Derivadas Para Aproximar Funções
O simples fato geométrico de que a tangente a uma curva é uma boa aproximação da curva próximo ao ponto de tangência $P$, pode ser usado para obter valores aproximados de funções. [Figura 1] Vamos estimar o valor de uma função $f(x)$ quando...

- Demonstração Da Derivada Da Função Exponencial
Neste artigo, veremos como encontrar a derivada da função exponencial. Para isso utilizaremos limites e o conceito de derivada. Vamos demonstrar que, se $f(x)=e^x$, então sua derivada será $f '(x)=e^x$. Demonstração:Primeiramente, vamos provar...

- Demonstração Do Limite Fundamental Exponencial
O número e tem grande importância em diversos ramos das ciências, pois está presente em vários fenômenos naturais como por exemplo: crescimento populacional, crescimento de população de bactérias, datação por carbono, circuitos elétricos,...

- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...

Matemática