Matemática

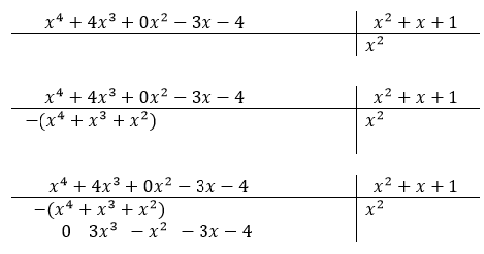
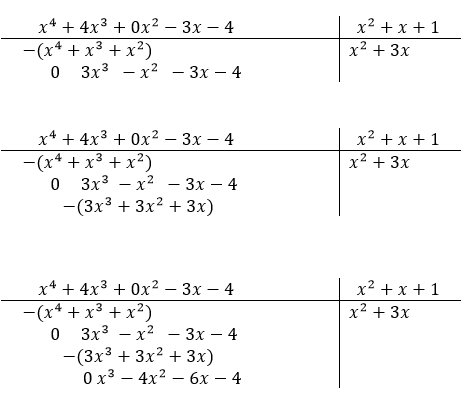
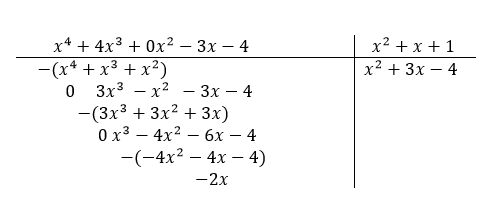

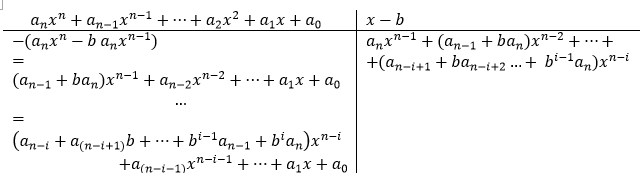

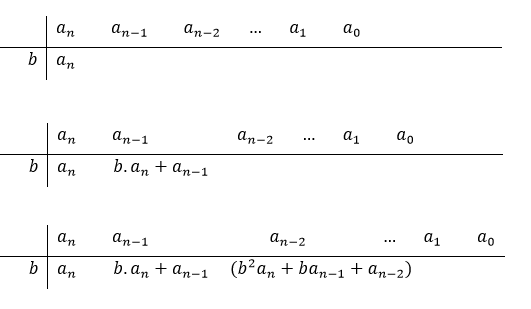
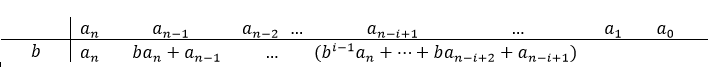
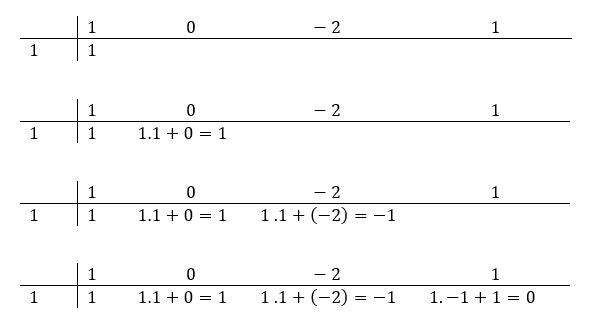
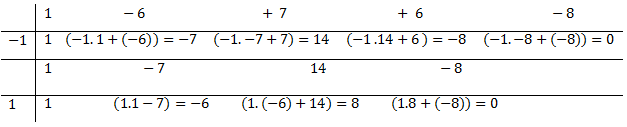
- Divisão De Polinômios
Dividir um polinômio f(x) (dividendo) por um g(x) (divisor diferente de 0) consiste em dividir f por g e determinar novos polinômios q(x) (quociente) e r (resto). Assim temos que f(x) = g(x).q(x) + r(x) e que o grau de q(x) será sempre menor que f(x)....
- Divisão De Polinômio Por Polinômio
O que vamos relembrar já foi exposto no texto “Divisão de polinômio por monômio”, mas vamos rever novamente: em toda divisão temos o dividendo, divisor, quociente e resto, como estamos falando de divisão de polinômio por polinômio, teremos:...
- Divisão De Polinômios
A operação de divisões é composta por dividendo, divisor, quociente e resto, no caso da divisão de polinômio por polinômio, considerando que cada um deles seja formado por mais de um monômio, iremos considerar a seguinte divisão: P(x) |G(x) R(x)...
- Divisão Inteira De Polinómios
O que vamos relembrar já foi exposto no texto “Divisão de polinômio por monômio”, mas vamos rever novamente: em toda divisão temos o dividendo, divisor, quociente e resto, como estamos falando de divisão de polinômio por polinômio, teremos:...
- Divisão De Polinômio Por Polinômio
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
Matemática
Polinômios - Divisão e o algoritmo de Briot-Ruffini
Olá pessoal, hoje vou falar sobre divisão de polinômios.
Assim como na divisão Euclidiana, ao dividir "a" por "p" temos a = p.q + r onde r é menor que p.
ao dividirmos um polinômio p(x) por outro g(x) temos: 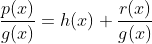 onde
onde  tem grau menor que o de
tem grau menor que o de  . Escrevendo de outra forma, temos:
. Escrevendo de outra forma, temos:  .
.
Observe que dados p(x) e h(x) só há 1 par de polinômios h(x) e r(x) que satisfazem com o grau de r(x) menor que o de g(x)- tente demonstrar isso - (a dica é demonstrar por absurdo). Onde p(x) é o dividendo, g(x) é o divisor, h(x) é o coeficiente e r(x) é o resto.
com o grau de r(x) menor que o de g(x)- tente demonstrar isso - (a dica é demonstrar por absurdo). Onde p(x) é o dividendo, g(x) é o divisor, h(x) é o coeficiente e r(x) é o resto.
Assim, é conveniente desenvolver um método para achar esses dois polinômios.
O método que todos aprendem na escola é a divisão polinomial. Mostrarei como funciona através de um exemplo.
Suponha que queiramos dividir  por
por 
Primeiramente coloque-os dispostos da seguinte forma:

Depois, vamos achar o primeiro termo do quociente (h(x)). Ele deve ser tal que ele multiplicado pelo termo de maior grau do divisor resulte no termo de maior grau do dividendo. Nesse caso, é  . Então, multiplicamos todo o divisor por esse termo encontrado e subtraímos do dividendo.
. Então, multiplicamos todo o divisor por esse termo encontrado e subtraímos do dividendo.
Segue as 3 operações feitas na sequência.
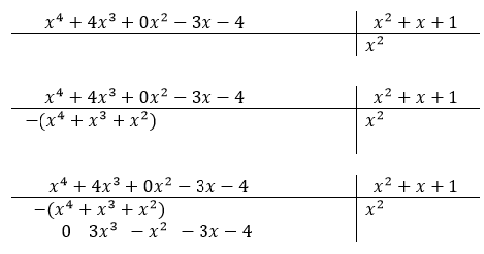
Agora, o próximo termo do quociente é tal que ao ser multiplicado pelo termo de maior grau do divisor dê  .
.
Nesse caso, o termo é  . Depois, multiplicamos o termo encontrado (
. Depois, multiplicamos o termo encontrado ( ) pelo divisor e subtraímos novamente.
) pelo divisor e subtraímos novamente.
Segue os passos descritos.
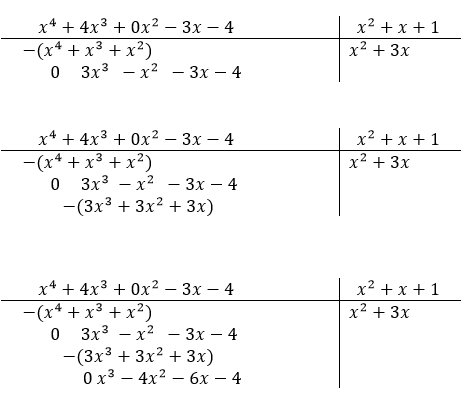
Agindo da mesma forma que fizemos pra achar os 2 primeiros termos vemos que o próximo é  . Segue os passos finais.
. Segue os passos finais.
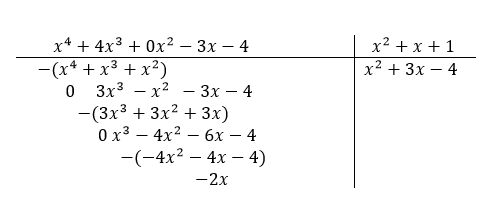
Assim, 
Observe que, somando 2x dos dois lados temos: 
Então, as raízes de  são as raízes de
são as raízes de  e
e  .
.
Há uma forma prática de dividir um polinômio por outro da forma g(x)=(x-b). Esse é o método de Briot-Ruffini, muito usado para testar se "b" é raiz de uma equação.
Primeiramente, vamos dividir um polinômio  por um da forma
por um da forma  e ver o que ocorre em cada passo.
e ver o que ocorre em cada passo.
Abaixo encontrando os 2 primeiros termos teremos

Logo, após encontrar o i-ésimo termo teremos:
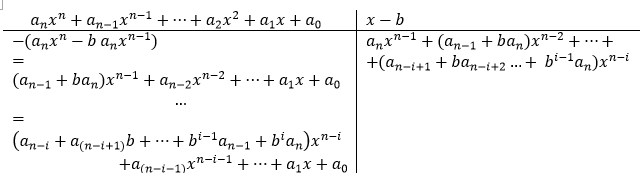
Deixo a demostração disso com o leitor senão o post fica muito extenso. A dica é usar indução (clique aqui para ler sobre o princípio da indução finita) verifique que pra i=1 é verdade e mostre que se vale para i=k então vale para i=k+1 (é só continuar efetuando a divisão).
Então, o resto será  .
.
Observe que se  = 0
= 0
então b é raiz de 
O quociente será: 

Observe que o resto dessa divisão é um número e o quociente é um polinômio de grau n-1. Logo, para fazer essa divisão precisamos só obter os coeficientes do quociente e o resto (o que pode ser feito decorando essa fórmula geral que eu mostrei logo acima). Para isso que serve o algoritmo de Briot-Ruffini. É um jeito fácil de obter esses números sem decorar nada.
Funciona assim:
Se quiser dividir  por (x-b), comece da seguinte disposição.
por (x-b), comece da seguinte disposição.

Observe que se quisermos dividir por (x-b) colocamos b. E do lado os coeficientes do dividendo. Caso algum coeficiente seja nulo, coloque 0.
Repita o primeiro coeficiente do dividendo ( ) multiplique por b e some com
) multiplique por b e some com  . Depois, coloque o resultado dessa soma abaixo de
. Depois, coloque o resultado dessa soma abaixo de  . Multiplique esse resultado por b, some com
. Multiplique esse resultado por b, some com  e repita logo abaixo de
e repita logo abaixo de  . Seguem os passos descritos.
. Seguem os passos descritos.
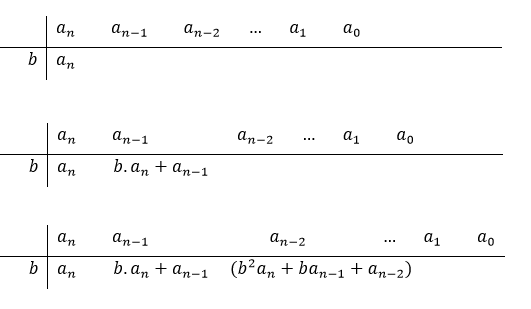
Observe que esses já são os 3 primeiros termos da divisão. Após encontrar o i-ésimo termo teremos:
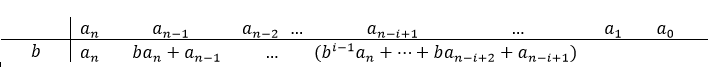
A demostração disso é por indução e é idêntica à anterior.
Observe que o último termo a ser escrito (abaixo de  ) será o resto da divisão. Se este termo for 0, então b é raiz do polinômio original.
) será o resto da divisão. Se este termo for 0, então b é raiz do polinômio original.
Assim, com esse método obteremos os coeficientes do quociente e o resto da divisão de forma mais rápida.
Ex: Suponha que queiramos dividir  por
por  . Nesse caso temos:
. Nesse caso temos:
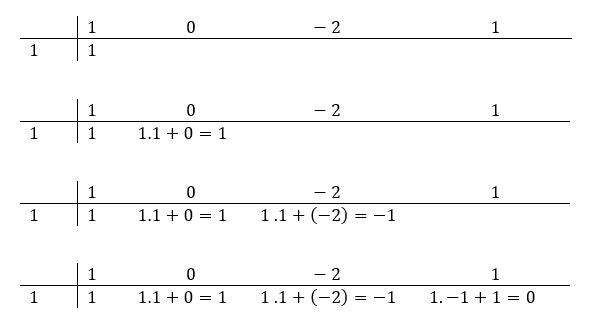
Assim,  .
.
Suponha que quiséssemos dividir  por
por  . Observe que
. Observe que  e -1 e 1 são raízes de
e -1 e 1 são raízes de  . Assim, podemos dividir
. Assim, podemos dividir  por (x+1) e depois dividir por (x-1)
por (x+1) e depois dividir por (x-1)
Temos:
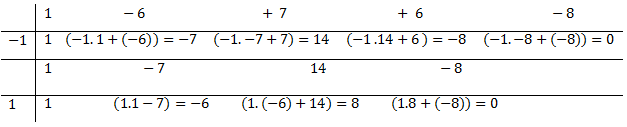
Logo,  .
.
Observe que só pudemos fazer isso por que são ambas raízes de  .
.
Bem, por hoje é só. Para fixar o conteúdo vale a pena fazer algumas divisões com polinômios aleatórios.
Se você gostou do blog, curta nossa página no Facebook e se inscreva por e-mail para não perder nenhuma atualização. Não se esqueça de avaliar a postagem logo abaixo, isso é muito importante para sabermos a qualidade do conteúdo que estamos produzindo.
Até mais.
- Divisão De Polinômios
Dividir um polinômio f(x) (dividendo) por um g(x) (divisor diferente de 0) consiste em dividir f por g e determinar novos polinômios q(x) (quociente) e r (resto). Assim temos que f(x) = g(x).q(x) + r(x) e que o grau de q(x) será sempre menor que f(x)....
- Divisão De Polinômio Por Polinômio
O que vamos relembrar já foi exposto no texto “Divisão de polinômio por monômio”, mas vamos rever novamente: em toda divisão temos o dividendo, divisor, quociente e resto, como estamos falando de divisão de polinômio por polinômio, teremos:...
- Divisão De Polinômios
A operação de divisões é composta por dividendo, divisor, quociente e resto, no caso da divisão de polinômio por polinômio, considerando que cada um deles seja formado por mais de um monômio, iremos considerar a seguinte divisão: P(x) |G(x) R(x)...
- Divisão Inteira De Polinómios
O que vamos relembrar já foi exposto no texto “Divisão de polinômio por monômio”, mas vamos rever novamente: em toda divisão temos o dividendo, divisor, quociente e resto, como estamos falando de divisão de polinômio por polinômio, teremos:...
- Divisão De Polinômio Por Polinômio
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
