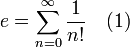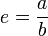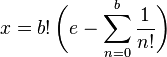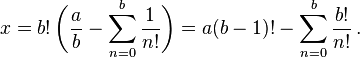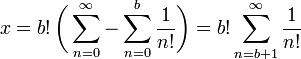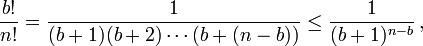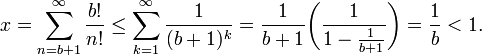Matemática

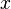 é obrigatoriamente um número inteiro pois pode ser escrito como:
é obrigatoriamente um número inteiro pois pode ser escrito como:
- Estrategias Para Provas De Teoremas
Fonte: http://www.inf.ufsc.br Elaborar provas de teoremas é um atividade que em geral não pode ser ensinada. A processo de construção de provas normalmente é aprendido por...
- Como Provar Que Log De 2 é Irracional?
Em postagens anteriores, tivemos ocasião de apresentar demonstrações para a irracionalidade de raiz de dois e para a irracionalidade de pi. Respondendo a pergunta de um leitor, demonstraremos, nesta postagem, a seguinte Proposição:...
- O Algoritmo Da Divisão Parte Iv [o Fim]
Esta é a última postagem da série que teve o objetivo de demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
- O Algoritmo Da Divisão Parte Ii
Nesta série de postagens estamos nos dedicando a demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
- Por Que ?2 é Irracional?
Esta postagem se dedica a mostrar que o número cujo quadrado vale 2 é irracional (usaremos dois argumentos para isso). Além disso mostraremos que ??2 é irracional (também por dois argumentos). Vejamos então porque raiz de dois é irracional:...
Matemática
Prova de Irracionalidade do Número de Euler

Na matemática, o número de Euler é uma das mais importantes constantes reais. A demonstração de que este número é irracional é considerada um dos mais elegantes teoremas de matemática. A demonstração baseia-se na representação do número de Euler pela série de Taylor da função exponencial em 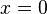 :
:
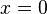 :
:Demonstração
Esta é uma prova por contradição. Inicialmente, assume-se que e é um número racional, ou seja, que pode ser escrito na forma:
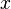 é obrigatoriamente um número inteiro pois pode ser escrito como:
é obrigatoriamente um número inteiro pois pode ser escrito como: Desta forma fica claro que 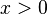 . Se pudermos provar que
. Se pudermos provar que 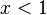 , o resultado está terminado, pois a contradição terá sido obtida, uma vez que não existe número inteiro maior que zero e menor que um.
, o resultado está terminado, pois a contradição terá sido obtida, uma vez que não existe número inteiro maior que zero e menor que um.
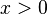 . Se pudermos provar que
. Se pudermos provar que 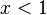 , o resultado está terminado, pois a contradição terá sido obtida, uma vez que não existe número inteiro maior que zero e menor que um.
, o resultado está terminado, pois a contradição terá sido obtida, uma vez que não existe número inteiro maior que zero e menor que um.Prova-se agora que 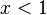 , observando que para cada termo
, observando que para cada termo 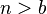 , vale a estimativa:
, vale a estimativa:
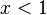 , observando que para cada termo
, observando que para cada termo 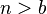 , vale a estimativa:
, vale a estimativa:Introduz-se a mudança de variável 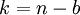 e usa-se soma dos termos de uma progressão geométrica:
e usa-se soma dos termos de uma progressão geométrica:
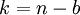 e usa-se soma dos termos de uma progressão geométrica:
e usa-se soma dos termos de uma progressão geométrica:E o resultado segue, pois como é fácil ver 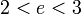 , o que implica que
, o que implica que  não é um número inteiro e, portanto,
não é um número inteiro e, portanto, 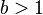 .
.
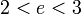 , o que implica que
, o que implica que  não é um número inteiro e, portanto,
não é um número inteiro e, portanto, 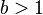 .
.Referências
Aigner, Martin; Ziegler, Günter. Proofs from THE BOOK. Berlin; New York: Springer, 2003. ISBN 3-540-40460-0- Estrategias Para Provas De Teoremas
Fonte: http://www.inf.ufsc.br Elaborar provas de teoremas é um atividade que em geral não pode ser ensinada. A processo de construção de provas normalmente é aprendido por...
- Como Provar Que Log De 2 é Irracional?
Em postagens anteriores, tivemos ocasião de apresentar demonstrações para a irracionalidade de raiz de dois e para a irracionalidade de pi. Respondendo a pergunta de um leitor, demonstraremos, nesta postagem, a seguinte Proposição:...
- O Algoritmo Da Divisão Parte Iv [o Fim]
Esta é a última postagem da série que teve o objetivo de demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
- O Algoritmo Da Divisão Parte Ii
Nesta série de postagens estamos nos dedicando a demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
- Por Que ?2 é Irracional?
Esta postagem se dedica a mostrar que o número cujo quadrado vale 2 é irracional (usaremos dois argumentos para isso). Além disso mostraremos que ??2 é irracional (também por dois argumentos). Vejamos então porque raiz de dois é irracional:...