Matemática
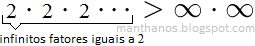
O que é maior: um produto de infinitos fatores, cada um igual a 2 ou um produto de apenas dois fatores, cada um igual ao infinito?
A pergunta acima reflete apenas um caso particular do problema que iremos propor: se a é um número real maior do que 1 e se e b é um número natural qualquer (eventualmente iguais, tal qual no título desta postagem) então quem é maior: a? (um produto de infinitos fatores iguais a a) ou ?b (um produto de b fatores iguais ao infinito)?
- Qual é A Probabilidade De Ter Raízes Reais?
PERGUNTA Quem sabe resolver este exercício? Dada a equação do 2° grau x² + bx + 4 = 0, escolhendo-se o número "b" ao acaso no conjunto {?10, ?8, ?6, ?4, ?2, 0, 2, 4, 6, 8} a probabilidade de que a equação formada admita raízes...
- O Algoritmo Da Divisão Parte Iv [o Fim]
Esta é a última postagem da série que teve o objetivo de demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- Equação De 2º Grau
1. Calcular o discriminante de cada equação e analisar as raízes em cada caso:a) x² + 9 x + 8 = 0 (R:-1 e -8) b) 9 x² - 24 x + 16 = 0 (R:4/3) c) x² - 2 x...
- NÚmeros Primos
Os números que admitem apenas dois divisores (ele próprio e 1 ) são chamados de números primos. exemplos a) 2 é um número primo, pois D2 = { 1,2} b) 3 é um número primo, pois D3 = { 1,3} c) 5 é um número primo, pois D5 = { 1,5} d) 7 é um número...
Matemática
Quem é maior: 2^? ou ?^2? ("dois elevado ao infinito" ou "infinito ao quadrado"?)
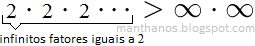
Na verdade a pergunta do modo como está formulada não faz muito sentido, pois ? não é um número (e, geralmente, quando falamos em potências estamos lidando com números). Mas vamos explicar o que ela está querendo significar. Para tanto observe a seguinte tabela que mostra o caso do título (o caso em que a = 2 e b = 2):
A tabela acima nos sugere que a partir da quinta linha o número 2n é sempre maior do que o número n². Deste modo, para números arbitrariamente grandes sempre temos 2n > n². Daí vem a "brincadeira" da figura inicial, na qual escrevemos 2? > ?² (o que, no nosso texto, significa que para um natural m suficientemente grande sempre tem-se 2n > n², desde que n seja maior do que m. Neste caso, olhando para a tabela concluímos que é suficiente que m seja igual a quatro. Em outros termos: se n > 4 então 2n > n²).
Vejamos agora um outro caso, o caso em que a = 5 e b = 8:
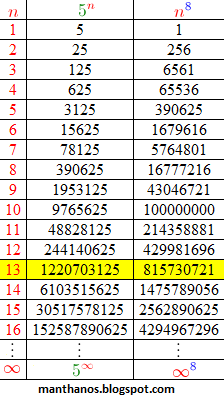Neste caso, conforme nos sugere a tabela, o número 5n só será maior do que n8 a partir da décima terceira linha.
Vejamos um terceiro caso, no qual a = 3 e b = 8.
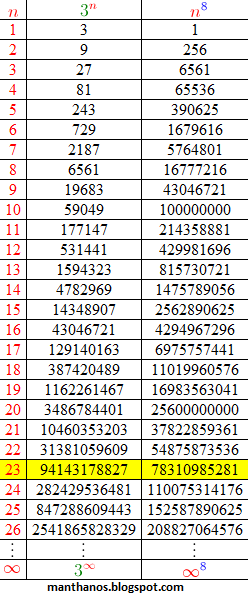No caso acima, a tabela nos induz a crer que é necessário n ser maior do que vinte e dois para se ter 3n > n8.
Comparando as tabelas podemos notar que, aparentemente, quanto mais b for maior do que a, tanto mais vai demorar para que se tenha an > nb (se colocássemos, por exemplo, a = 2 e b = 25 então a referida desigualdade só ocorreria na centésima noningentésima linha!). Imagine, agora, se colocássemos a = 2 e b = 1000000. Será que haveria uma linha a partir da qual 2n seria sempre maior do que n1000000? Com esta motivação fazemos a seguinte
PERGUNTA: Para quaisquer que sejam os valores de a e b (desde que seja a > 1 e b ? ?) sempre existe uma linha a partir da qual an > nb (independentemente de quão maior do que a seja b)? Em outros termos: escolhendo de modo totalmente arbitrário os valor de a e b, exceto pela restrição já mencionada, sembre é possível encontrar um natural m tal que an é maior do que nb para todo natural n maior do que m?
Dizer que não significa que é possível montar uma tabela (parecida com aquelas que foram apresentadas acima) na qual, numa mesma linha, o valor da coluna central será sempre menor do que o valor da coluna da direita. Por outro lado, dizer que sim significa que em qualquer tabela, se escrevermos um número suficiente de linhas vamos encontrar uma delas a partir da qual o valor da coluna central será sempre maior do que o valor da coluna da direita.
Confira uma resposta em breve aqui no BLOG MANTHANO.
Observação: grosso modo, pode-se dizer que para qualquer natural k, k? é infinito assim como ?k, logo não faz sentido dizer que um é maior do que o outro. Então, que fique claro: quando usamos o "infinito" nas perguntas, nas desigualdades e nas tabelas acima ele representou um número arbitrariamente grande.
Referências: na postagem da solução.
Erros podem ser relatados aqui.
Vejamos agora um outro caso, o caso em que a = 5 e b = 8:
Vejamos um terceiro caso, no qual a = 3 e b = 8.
Comparando as tabelas podemos notar que, aparentemente, quanto mais b for maior do que a, tanto mais vai demorar para que se tenha an > nb (se colocássemos, por exemplo, a = 2 e b = 25 então a referida desigualdade só ocorreria na centésima noningentésima linha!). Imagine, agora, se colocássemos a = 2 e b = 1000000. Será que haveria uma linha a partir da qual 2n seria sempre maior do que n1000000? Com esta motivação fazemos a seguinte
PERGUNTA: Para quaisquer que sejam os valores de a e b (desde que seja a > 1 e b ? ?) sempre existe uma linha a partir da qual an > nb (independentemente de quão maior do que a seja b)? Em outros termos: escolhendo de modo totalmente arbitrário os valor de a e b, exceto pela restrição já mencionada, sembre é possível encontrar um natural m tal que an é maior do que nb para todo natural n maior do que m?
Dizer que não significa que é possível montar uma tabela (parecida com aquelas que foram apresentadas acima) na qual, numa mesma linha, o valor da coluna central será sempre menor do que o valor da coluna da direita. Por outro lado, dizer que sim significa que em qualquer tabela, se escrevermos um número suficiente de linhas vamos encontrar uma delas a partir da qual o valor da coluna central será sempre maior do que o valor da coluna da direita.
Confira uma resposta em breve aqui no BLOG MANTHANO.
Observação: grosso modo, pode-se dizer que para qualquer natural k, k? é infinito assim como ?k, logo não faz sentido dizer que um é maior do que o outro. Então, que fique claro: quando usamos o "infinito" nas perguntas, nas desigualdades e nas tabelas acima ele representou um número arbitrariamente grande.
Referências: na postagem da solução.
Erros podem ser relatados aqui.
- Qual é A Probabilidade De Ter Raízes Reais?
PERGUNTA Quem sabe resolver este exercício? Dada a equação do 2° grau x² + bx + 4 = 0, escolhendo-se o número "b" ao acaso no conjunto {?10, ?8, ?6, ?4, ?2, 0, 2, 4, 6, 8} a probabilidade de que a equação formada admita raízes...
- O Algoritmo Da Divisão Parte Iv [o Fim]
Esta é a última postagem da série que teve o objetivo de demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- Equação De 2º Grau
1. Calcular o discriminante de cada equação e analisar as raízes em cada caso:a) x² + 9 x + 8 = 0 (R:-1 e -8) b) 9 x² - 24 x + 16 = 0 (R:4/3) c) x² - 2 x...
- NÚmeros Primos
Os números que admitem apenas dois divisores (ele próprio e 1 ) são chamados de números primos. exemplos a) 2 é um número primo, pois D2 = { 1,2} b) 3 é um número primo, pois D3 = { 1,3} c) 5 é um número primo, pois D5 = { 1,5} d) 7 é um número...