Matemática
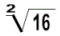 lê-se: raiz quadrada de 16.
lê-se: raiz quadrada de 16.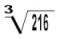 lê-se: raiz cúbica de 216.
lê-se: raiz cúbica de 216.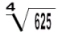 lê-se: raiz quarta raiz de 625.
lê-se: raiz quarta raiz de 625. lê-se: décima raiz de 1024.
lê-se: décima raiz de 1024.
dezenas multiplicadas pelas unidades, mais o quadrado das unidades.
Algarismos das unidades. Desde que o producto das dezenas multiplicadas por um numero inteiro de unidades nunca póde ser inferior a 10, podemos separar do resto 176 o algarismo das unidades, que é 6, para operarmos sómente com as 17 dezenas completas.
Sendo as 17 dezenas duas vezes o producto das dezenas multiplicadas pelas unidades, segue-se que se dividirmos 17 por duas vezes as dezenas, isto é, por 2 + 2 = 4, obteremos o algarismo das unidades. Ora, 17 / 4 = 4, portanto 4 é o algarismo das unidades da raiz.
Resta agora verificar se o resto 176 contém 2 (20 X 4) = 160, mais 4 X 4 = 16. Ora 160 + 16 = 176, e do resto 176 subtrahindo 176, nada resta.
Fica, portanto, demonstrado que 576 é um quadrado perfeito, e que a sua raiz quadrada é 24.
- Raiz Quadrada
Chama-se raiz quadrada de um número natural, um segundo número natural cujo o quadrado é igual ao número dado. Exemplos: a) √49 = 7 porque 7² = 49 b) √100 = 10 porque 10² = 100 NÚMEROS QUADRADOS PERFEITOS Vamos calcular os quadrados dos...
- Raiz Quadrada
Raiz quadrada Raiz quadrada de um número real não negativo x é o número real não negativo que, quando multiplicado por si próprio, iguala a x. Raiz quadrada de certa forma, lembra um pouco a Potenciação, por exemplo, no caso desse exercício de...
- Raiz Quadrada
Raiz quadrada de um número real não negativo x é o número real não negativo que, quando multiplicado por si próprio, iguala a x. Raiz quadrada de certa forma, lembra um pouco a Potenciação, por exemplo, no caso desse exercício de potenciação:...
- Fatorar
Fatorar é o mesmo que decompor o número em fatores primos, isto é, escrever um número através da multiplicação de números primos. Na fatoração utilizamos os números primos obedecendo a uma ordem crescente de acordo com as regras de divisibilidade...
- Fatoração
Exercícios Resolvidos de Fatoração Algébrica Exemplo 19) Fatore c2 - 2bc - a2 + b2 Reagrupando o polinômio, teremos : b2 - 2bc + c2 - a2 = (b2 - 2bc + c2) - a2 O trinômio b2 - 2bc + c2 pode ser fatorado como : (b - c)2 E dessa forma, teremos a...
Matemática
Raiz quadrada
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email [email protected]
Blog HTTP://ensinodematemtica.blogspot.com
http://accbarrosogestar.blogspot.com.br
http://accbarrosogestar.blogspot.com.br
www.accbarrosogestar.wordpress.com
Raiz de um numero é um dos fatores iguais que produziram esse numero.
As raízes, bem como as potências, distinguem-se pelo seu grau como raiz quadrada ou segunda raiz, raiz cúbica ou terceira raiz, quarta, raiz, quinta, raiz, etc.
Raiz quadrada de um numero é um dos dois fatores iguais desse numero; assim a raiz quadrada de 25 é 5, porque 25 = 5 X 5.
Raiz cúbica de um numero é um dos três fatores iguais desse numero; assim a raiz cúbica de 64 é 4, porque 64 = 4 X 4 X 4.
A quarta raiz de um numero é um dos quatro fatores iguais desse numero; assim a quarta raiz de 81 é 3, porque 81 =
= 3 X 3 X 3 X 3
A figura  chama-se sinal radical, e quando está escrito sobre um numero, mostra que esse numero deve ser tomado na raiz indicada pelo índice.
chama-se sinal radical, e quando está escrito sobre um numero, mostra que esse numero deve ser tomado na raiz indicada pelo índice.
 chama-se sinal radical, e quando está escrito sobre um numero, mostra que esse numero deve ser tomado na raiz indicada pelo índice.
chama-se sinal radical, e quando está escrito sobre um numero, mostra que esse numero deve ser tomado na raiz indicada pelo índice.Índice é o numero escrito no ângulo do sinal radical, para mostrar o grau da raiz; assim
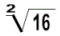 lê-se: raiz quadrada de 16.
lê-se: raiz quadrada de 16.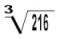 lê-se: raiz cúbica de 216.
lê-se: raiz cúbica de 216.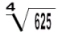 lê-se: raiz quarta raiz de 625.
lê-se: raiz quarta raiz de 625. lê-se: décima raiz de 1024.
lê-se: décima raiz de 1024.Nota. O sinal  é uma corrupção da lettra r , inicial da palavra latina radix que significa raiz.
é uma corrupção da lettra r , inicial da palavra latina radix que significa raiz.
 é uma corrupção da lettra r , inicial da palavra latina radix que significa raiz.
é uma corrupção da lettra r , inicial da palavra latina radix que significa raiz.Na raiz quadrada escreve-se simplesmente o sinal  , ficando subentendido o índice 2.
, ficando subentendido o índice 2.
 , ficando subentendido o índice 2.
, ficando subentendido o índice 2.Qualquer raiz de 1 é sempre 1, porque 1 X 1 X 1 = 1.
Os quadrados perfeitos desde 1 até 100 são os seguintes:
| Quadrados perfeitos: | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
| Raizes quadradas: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Vemos aqui que desde 1 até 100 ha só dez números inteiros que são quadrados perfeitos, isto é, produtos de dois fatores iguais, e até 1000, ha só trinta e um; todos os outros números intermediários não são quadrados. Daqui se originou a divisão dos números inteiros em quadrados perfeitos e quadrados imperfeitos.
Quadrado perfeito é o numero cuja raiz quadrada pode ser exatamente determinada; assim 64 é um quadrado perfeito, porque tem uma raiz exata, que é 8.
Quadrado imperfeito é o numero cuja raiz quadrada não pode ser exatamente determinada; assim a raiz quadrada de 10 é 3, 1622 ... , isto é, um numero inteiro e uma fração. Esta raiz, por mais aproximada que seja, multiplicada por si, não produzirá exatamente o numero 10, e por isso tem o nome de raiz surda, para distingui-la da raiz exata dos quadrados perfeitos.Pela simples inspeção de um numero qualquer, não podemos saber se ele é ou não quadrado perfeito, sem extrair-mos a sua raiz quadrada; temos, porém, alguns dados ou teoremas que nos fazem conhecer de antemão que certos números não são quadrados. Esses teoremas são os seguintes:
| 1. Teorema. Todo numero terminado em 2, 3, 7 ou 8, não é quadrado perfeito. Demonstração. O algarismo em que termina um quadrado representa as unidades de um produto de dois números iguais, isto é, o produto da raiz quadrada multiplicada por si mesma. Ora o produto de dois números iguais acaba sempre em 1, 4, 5, 6, 9 ou 0. Portanto os números terminados em 2, 3, 7 ou 8 não são quadrados perfeitos, porque não podem ser o produto de dois números iguais. |
| 2. Teorema. Todo numero terminado por um numero impar de cifras não é quadrado perfeito. Demonstração. Sendo um quadrado sempre o produto de dois fatores iguais, quando um fator termina em uma, duas ou mais cifras, o quadrado terá o dobro dessas cifras, e por isso elas estarão em um quadrado sempre em numero par; e assim podemos já saber de antemão que os números 1000, 400000 e 750 não são quadrados perfeitos. |
| 3. Teorema. Todo numero par que não for divisível por 4, não é quadrado perfeito. Demonstração. Todo o numero par é divisível por 2, e se um numero par for multiplicado por si mesmo, será divisível por 2, e por 2 X 2 = 4. Deste modo, já podemos saber que 322 e 1334 não são quadrados perfeitos. |
| 4. Teorema. Todo numero terminado em 5, e que nas dezenas não tem o algarismo 2, não é quadrado perfeito. Demonstração. Um numero terminado em 5 só pode ter uma raiz terminada em 5, quando tem o algarismo 2 nas dezenas, porque o produto de dois números iguais terminados em 5 finaliza sempre pelos algarismos 25. |
Extração da raiz quadrada
Extrair a raiz quadrada de um numero é achar o fator que, multiplicado por si, produz esse numero.
Se dividirmos um numero em classes de dois algarismos, começando pela direita, conheceremos logo quantos algarismos tem a sua raiz quadrada; assim o numero 55696 dividido em classes de dois algarismos, que são 5.56.95 mostra logo que a sua raiz quadrada tem três algarismos, porque este numero consta de três classes; o numero 8649, como consta de duas classes, que são 86.49, a sua raiz tem dois algarismos, etc. A ultima classe, que é a da esquerda, pode ter um ou dois algarismos; as outras classes devem ser sempre dois. Daqui podemos deduzir o seguinte principio:
Quantas classes tiver um numero, tantos algarismos terá a sua raiz quadrada.
Problema. Qual é a raiz quadrada de 576?
Solução analítica. O numero 576, como consta de duas classes, já sabemos que a sua raiz quadrada tem dois algarismos, sendo um das dezenas e o outro das unidades. Precisamos portanto achar o algarismo das dezenas, e depois, o algarismo das unidades.
Algarismos das dezenas. Como já demonstramos na secção 373, o numero 576, sendo quadrado perfeito, deve conter primeiro o quadrado das dezenas, segundo duas vezes o produto das dezenas multiplicadas pelas unidades, terceiro o quadrado das unidades.
Formação sintética de um quadrado Um quadrado pode ser também considerado como um conjunto ou soma de parcelas diversas que conservam entre si certa relação, e que podem ser de novo desagregadas por meio de uma decomposição analítica do quadrado. As diversas partes ou elementos que constituem um quadrado e a relação que ha entre elles estão claramente indicadas no seguinte teorema: O quadrado da soma de dois numero é igual á soma do quadrado do primeiro numero, mais duas vezes o produto do primeiro multiplicado pelo segundo, e mais o quadrado do segundo. Este teorema ficará perfeitamente claro com a seguinte ilustração: Ilustração. Se tomarmos o numero 15, e o dividirmos em dois números quaisquer, como, por exemplo, 8 + 7, e seguirmos depois o processo indicado pelo theorema acima exposto, teremos o seguinte resultado:
Por uma simples inspecção, vemos que o quadrado de 15 é igual a somma das tres parcellas obtidas por meio dos numeros 8 e 7. Isto é, 15 ao quadrado = (8 X 8) + (8 X 7) + (8 X 7) + (7 X 7) ou 64 + 112 + 49 = 225. A expressão (8 X 7) + (8 X 7) pode ser simplificada ou reduzida a 2 (8 X 7) que exprime exactamente o mesmo valor, porque quer dizer duas vezes o producto de 8 multiplicado por 7, isto é, duas vezes 56 ou 2 X 56. Se dermos ao numero 15 outra formação qualquer, o resultado será o mesmo; assim
Se, em lugar de 15, operarmos com outro numero qualquer, acharemos a mesma relação entre o quadrado desse numero e as duas parcellas que o formarem. Por este processo synthetico agrupamos ou reunimos em uma somma todas as partes que formam um quadrado; e por um processo opposto, poderemos decompor ou separar novamente essas partes para, por meio dellas, achar a raiz do quadrado. Deste ultimo processo trataremos mais adiante. |
| A classe da esquerda, que é 5, contém o quadrado das dezenas, porque dezenas multiplicadas por dezenas dão centenas. O quadrado perfeito mais approximado de 5 é 4, e a raiz de 4 é 2; 2 é o algarismo das dezenas da raiz. Ora o quadrado de 2 é 2 X 2 = 4, e subtrahindo 4 de 5, resta uma centena que com a classe seguinte fórma o resto 176. Como já sahiu o quadrado das dezenas, este resto deve conter duas vezes o producto das |  |
Algarismos das unidades. Desde que o producto das dezenas multiplicadas por um numero inteiro de unidades nunca póde ser inferior a 10, podemos separar do resto 176 o algarismo das unidades, que é 6, para operarmos sómente com as 17 dezenas completas.
Sendo as 17 dezenas duas vezes o producto das dezenas multiplicadas pelas unidades, segue-se que se dividirmos 17 por duas vezes as dezenas, isto é, por 2 + 2 = 4, obteremos o algarismo das unidades. Ora, 17 / 4 = 4, portanto 4 é o algarismo das unidades da raiz.
Resta agora verificar se o resto 176 contém 2 (20 X 4) = 160, mais 4 X 4 = 16. Ora 160 + 16 = 176, e do resto 176 subtrahindo 176, nada resta.
Fica, portanto, demonstrado que 576 é um quadrado perfeito, e que a sua raiz quadrada é 24.
- Raiz Quadrada
Chama-se raiz quadrada de um número natural, um segundo número natural cujo o quadrado é igual ao número dado. Exemplos: a) √49 = 7 porque 7² = 49 b) √100 = 10 porque 10² = 100 NÚMEROS QUADRADOS PERFEITOS Vamos calcular os quadrados dos...
- Raiz Quadrada
Raiz quadrada Raiz quadrada de um número real não negativo x é o número real não negativo que, quando multiplicado por si próprio, iguala a x. Raiz quadrada de certa forma, lembra um pouco a Potenciação, por exemplo, no caso desse exercício de...
- Raiz Quadrada
Raiz quadrada de um número real não negativo x é o número real não negativo que, quando multiplicado por si próprio, iguala a x. Raiz quadrada de certa forma, lembra um pouco a Potenciação, por exemplo, no caso desse exercício de potenciação:...
- Fatorar
Fatorar é o mesmo que decompor o número em fatores primos, isto é, escrever um número através da multiplicação de números primos. Na fatoração utilizamos os números primos obedecendo a uma ordem crescente de acordo com as regras de divisibilidade...
- Fatoração
Exercícios Resolvidos de Fatoração Algébrica Exemplo 19) Fatore c2 - 2bc - a2 + b2 Reagrupando o polinômio, teremos : b2 - 2bc + c2 - a2 = (b2 - 2bc + c2) - a2 O trinômio b2 - 2bc + c2 pode ser fatorado como : (b - c)2 E dessa forma, teremos a...
