Matemática
Construção
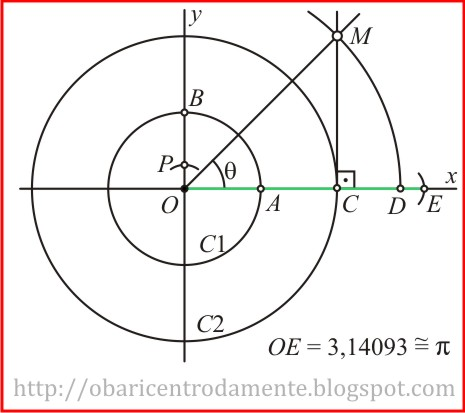
$1)$ Inicie a construção num eixo ortogonal $xOy$;
$2)$ Descreva a circunferência $C_1$ de centro $O$ e raio $1$ e marque os ponto $A$ e $B$ na intersecção com as retas $Ox$ e $Oy$, respectivamente;
$3)$ Descreva a circunferência $C_2$ de centro $O$ e raio $2OA = 2$ e marque o ponto $C$ na intersecção com a reta $Ox$;
$4)$ Trace a bissetriz do ângulo $AOB$. Assim o ângulo $\theta=45°$;
$5)$ Suba a perpendicular ao eixo $x$ por $C$ e marque o ponto $M$ na intersecção com a bissetriz;
$6)$ Descreva um arco de raio $OM$ centrado em $O$ e marque o ponto $D$ na intersecção com a reta $Ox$;
$7)$ Construindo sucessivas mediatrizes convenientes, encontramos o ponto $P$ em $Oy$ de modo que $OP$ seja $5/16$ do raio de $C_1$;
$8)$ Com raio $OP$ e centro em $D$, descreva um arco marcando o ponto $E$ na intersecção com $Ox$.
$9)$ O Segmento $OE$ aproxima $\pi$ em $3,14093$.
Demonstração
Como o ângulo $\theta=45°$ e $CM$ é ortogonal ao eixo $x$, temos que $OC = CM = 2$. Assim:
\begin{matrix}
OM^2=OC^2+CM^2\\
OM^2=4+4\\
OM=2\sqrt{2}
\end{matrix}
Vejam que $OM = OD$. O segmento $OE = OD + DE$. O segmento $OD$ já encontramos e o segmento $DE = OP = 5/16$. Assim:
\begin{matrix}
OE=OD+DE\\
OE=2\sqrt{2}+\frac{5}{16}\\
OE=3,14093 \cong \pi
\end{matrix}
Veja mais:
Retificação da Circunferência (Parte 1)
Retificação da Circunferência (Parte 2) - Método de Kochanski
Retificação da Circunferência (Parte 3) - Método de Gelder
- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...
- Retificação Da Circunferência (parte 6) – Método De Specht
Wilhelm Otto Ludwing Specht (1907-1985) foi um matemático alemão que desenvolveu uma construção geométrica que aproxima a retificação da circunferência com uma precisão de 5 casas decimais. Construção: 1) Descreva uma circunferência de raio...
- Retificação Da Circunferência (parte 5)
A retificação da circunferência é um tema que me fascinou desde a primeira vez que li sobre o assunto. Está diretamente relacionado à quadratura do círculo, que foi provado sua impossibilidade por meios da geometria euclidiana. Fico tentando algumas...
- Construção De Um Heptágono Regular Com Régua E Compasso (parte 1)
O Heptágono regular foi fonte de muito mistério na Geometria, quanto à sua construção com régua e compasso, apenas. Gaus provou aos $19$ anos que o heptadecágono regular é construtível com régua e compasso. De seus estudos sobre a contrutibilidade...
- Construção De Um Pentágono Regular Com Régua E Compasso (parte Iii)
Neste post vou mostrar uma terceira maneira de construir um pentágono regular utilizando régua e compasso. Para ver as construções anteriores, clique em Parte I e Parte II. Para esta construção, comece traçando um segmento de reta AB que será...
Matemática
Retificação da Circunferência (Parte 4)
Ficou provado que é impossível a construção de um quadrado com mesma área que um círculo utilizando instrumentos euclidianos. O que conseguimos são somente boas aproximações. Encontrar um segmento de reta que aproxime $\pi$ também mobiliza muitos matemáticos.
Este método que apresento aqui foi desenvolvido por mim e aproxima $\pi$ em duas casas decimais, levando ao valor de $3,14093$. Vamos ver como se constrói este segmento.

Construção
$1)$ Inicie a construção num eixo ortogonal $xOy$;
$2)$ Descreva a circunferência $C_1$ de centro $O$ e raio $1$ e marque os ponto $A$ e $B$ na intersecção com as retas $Ox$ e $Oy$, respectivamente;
$3)$ Descreva a circunferência $C_2$ de centro $O$ e raio $2OA = 2$ e marque o ponto $C$ na intersecção com a reta $Ox$;
$4)$ Trace a bissetriz do ângulo $AOB$. Assim o ângulo $\theta=45°$;
$5)$ Suba a perpendicular ao eixo $x$ por $C$ e marque o ponto $M$ na intersecção com a bissetriz;
$6)$ Descreva um arco de raio $OM$ centrado em $O$ e marque o ponto $D$ na intersecção com a reta $Ox$;
$7)$ Construindo sucessivas mediatrizes convenientes, encontramos o ponto $P$ em $Oy$ de modo que $OP$ seja $5/16$ do raio de $C_1$;
$8)$ Com raio $OP$ e centro em $D$, descreva um arco marcando o ponto $E$ na intersecção com $Ox$.
$9)$ O Segmento $OE$ aproxima $\pi$ em $3,14093$.
Demonstração
Como o ângulo $\theta=45°$ e $CM$ é ortogonal ao eixo $x$, temos que $OC = CM = 2$. Assim:
\begin{matrix}
OM^2=OC^2+CM^2\\
OM^2=4+4\\
OM=2\sqrt{2}
\end{matrix}
Vejam que $OM = OD$. O segmento $OE = OD + DE$. O segmento $OD$ já encontramos e o segmento $DE = OP = 5/16$. Assim:
\begin{matrix}
OE=OD+DE\\
OE=2\sqrt{2}+\frac{5}{16}\\
OE=3,14093 \cong \pi
\end{matrix}
Veja mais:
Retificação da Circunferência (Parte 1)
Retificação da Circunferência (Parte 2) - Método de Kochanski
Retificação da Circunferência (Parte 3) - Método de Gelder
- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...
- Retificação Da Circunferência (parte 6) – Método De Specht
Wilhelm Otto Ludwing Specht (1907-1985) foi um matemático alemão que desenvolveu uma construção geométrica que aproxima a retificação da circunferência com uma precisão de 5 casas decimais. Construção: 1) Descreva uma circunferência de raio...
- Retificação Da Circunferência (parte 5)
A retificação da circunferência é um tema que me fascinou desde a primeira vez que li sobre o assunto. Está diretamente relacionado à quadratura do círculo, que foi provado sua impossibilidade por meios da geometria euclidiana. Fico tentando algumas...
- Construção De Um Heptágono Regular Com Régua E Compasso (parte 1)
O Heptágono regular foi fonte de muito mistério na Geometria, quanto à sua construção com régua e compasso, apenas. Gaus provou aos $19$ anos que o heptadecágono regular é construtível com régua e compasso. De seus estudos sobre a contrutibilidade...
- Construção De Um Pentágono Regular Com Régua E Compasso (parte Iii)
Neste post vou mostrar uma terceira maneira de construir um pentágono regular utilizando régua e compasso. Para ver as construções anteriores, clique em Parte I e Parte II. Para esta construção, comece traçando um segmento de reta AB que será...
