Matemática
![(\vec{u},\vec{v},\vec{w}) = \vec{u}\times \vec{v}\cdot \vec{w} \qquad (1) [;(\vec{u},\vec{v},\vec{w}) = \vec{u}\times \vec{v}\cdot \vec{w} \qquad (1);]](matematica/matematica-5631d15c18583.%20=%20%5Cvec%7Bu%7D%5Ctimes%20%5Cvec%7Bv%7D%5Ccdot%20%5Cvec%7Bw%7D%20%5Cqquad%20%281%29)
Sendo:
![\vec{u}\times \vec{v} =\begin{vmatrix}\vec{i} & \vec{j} & \vec{k}\\ x_1 & y_1 & z_1 \\x_2 & y_2 & z_2 \\ \end{bmatrix} = [;\vec{u}\times \vec{v} =\begin{vmatrix}\vec{i} & \vec{j} & \vec{k}\\ x_1 & y_1 & z_1 \\x_2 & y_2 & z_2 \\ \end{bmatrix} =;]](matematica/matematica-5631d15c99756.%5Ctimes%20%5Cvec%7Bv%7D%20=%5Cbegin%7Bvmatrix%7D%5Cvec%7Bi%7D%20&%20%5Cvec%7Bj%7D%20&%20%5Cvec%7Bk%7D%5C%5C%20x_1%20&%20y_1%20&%20z_1%20%5C%5Cx_2%20&%20y_2%20&%20z_2%20%5C%5C%20%5Cend%7Bbmatrix%7D%20=)
![= (y_1z_2 - y_2z_1)\vec{i} - (x_1z_2 - x_2z_1)\vec{j} + (x_1y_2 - x_2y_1)\vec{k} [;= (y_1z_2 - y_2z_1)\vec{i} - (x_1z_2 - x_2z_1)\vec{j} + (x_1y_2 - x_2y_1)\vec{k};]](matematica/matematica-5631d15c4b14b.)
![(\vec{u},\vec{v},\vec{w}) = \vec{u}\times \vec{v}\cdot \vec{w} = [;(\vec{u},\vec{v},\vec{w}) = \vec{u}\times \vec{v}\cdot \vec{w} = ;]](matematica/matematica-5631d15c18583.%20=%20%5Cvec%7Bu%7D%5Ctimes%20%5Cvec%7Bv%7D%5Ccdot%20%5Cvec%7Bw%7D%20=)
![= (y_1z_2 - y_2z_1)x_3 - (x_1z_2 - x_2z_1)y_3 + (x_1y_2 - x_2y_1)z_3 [;= (y_1z_2 - y_2z_1)x_3 - (x_1z_2 - x_2z_1)y_3 + (x_1y_2 - x_2y_1)z_3;]](matematica/matematica-5631d15c751c5.)
![=\begin{vmatrix}x_1 & y_1 & z_1\\ x_2 & y_2 & z_2 \\x_3 & y_3 & z_3 \\ \end{bmatrix} [; =\begin{vmatrix}x_1 & y_1 & z_1\\ x_2 & y_2 & z_2 \\x_3 & y_3 & z_3 \\ \end{bmatrix};]](http://thewe.net/tex/%20=%5Cbegin%7Bvmatrix%7Dx_1%20&%20y_1%20&%20z_1%5C%5C%20x_2%20&%20y_2%20&%20z_2%20%5C%5Cx_3%20&%20y_3%20&%20z_3%20%5C%5C%20%5Cend%7Bbmatrix%7D)
Exemplo 1: Calcule![(\vec{u},\vec{v},\vec{w}) [;(\vec{u},\vec{v},\vec{w});]](matematica/matematica-5631d15c18583.) , sendo
, sendo ![\vec{u} = (1,-1,2) [;\vec{u} = (1,-1,2);]](matematica/matematica-5631d15c99756.%20=%20%281,-1,2%29) ,
, ![\vec{v} = (2,0,1) [;\vec{v} = (2,0,1);]](matematica/matematica-5631d15ca8c0b.%20=%20%282,0,1%29) e
e ![\vec{w} = (-1,3,0) [;\vec{w} = (-1,3,0);]](matematica/matematica-5631d15cb6f1a.%20=%20%28-1,3,0%29) .
.
Resolução: Pela definição acima, temos;
![(\vec{u},\vec{v},\vec{w}) =\begin{vmatrix} 1 & -1 & 2\\ 2 & 0 & 1 \\ -1 & 3 & 0 \\ \end{bmatrix} = 10 [;(\vec{u},\vec{v},\vec{w}) =\begin{vmatrix} 1 & -1 & 2\\ 2 & 0 & 1 \\ -1 & 3 & 0 \\ \end{bmatrix} = 10;]](matematica/matematica-5631d15c18583.%20=%5Cbegin%7Bvmatrix%7D%201%20&%20-1%20&%202%5C%5C%202%20&%200%20&%201%20%5C%5C%20-1%20&%203%20&%200%20%5C%5C%20%5Cend%7Bbmatrix%7D%20=%2010)
![(\vec{v},\vec{u},\vec{w}) = (\vec{w},\vec{v},\vec{u}) = (\vec{u},\vec{w},\vec{v}) = \ldots = - (\vec{u},\vec{v},\vec{w}) [;(\vec{v},\vec{u},\vec{w}) = (\vec{w},\vec{v},\vec{u}) = (\vec{u},\vec{w},\vec{v}) = \ldots = - (\vec{u},\vec{v},\vec{w});]](matematica/matematica-5631d15d3c5d2.)
i)![(\vec{u_1} + \alpha \vec{u_2},\vec{v},\vec{w}) = (\vec{u_1},\vec{v},\vec{w}) + \alpha(\vec{u_2},\vec{v},\vec{w}) [;(\vec{u_1} + \alpha \vec{u_2},\vec{v},\vec{w}) = (\vec{u_1},\vec{v},\vec{w}) + \alpha(\vec{u_2},\vec{v},\vec{w});]](matematica/matematica-5631d15d4b63d.) ;
;
ii)![(\alpha \vec{u}, \beta \vec{v}, \gamma \vec{w}) = \alpha \beta \gamma (\vec{u},\vec{v},\vec{w}) [;(\alpha \vec{u}, \beta \vec{v}, \gamma \vec{w}) = \alpha \beta \gamma (\vec{u},\vec{v},\vec{w});]](matematica/matematica-5631d15d5a7ef.) ;
;
![(\vec{u},k\vec{u},\vec{w}) = 0 [;(\vec{u},k\vec{u},\vec{w}) = 0;]](matematica/matematica-5631d15d692c9.)
![\vec{u}\times \vec{v}\cdot \vec{w} = \vec{u}\cdot \vec{v} \times \vec{w} [;\vec{u}\times \vec{v}\cdot \vec{w} = \vec{u}\cdot \vec{v} \times \vec{w};]](matematica/matematica-5631d15c99756.%5Ctimes%20%5Cvec%7Bv%7D%5Ccdot%20%5Cvec%7Bw%7D%20=%20%5Cvec%7Bu%7D%5Ccdot%20%5Cvec%7Bv%7D%20%5Ctimes%20%5Cvec%7Bw%7D) .
.
Demonstração:
![\vec{u}\cdot \vec{v}\times \vec{w} = \vec{v}\times \vec{w}\cdot \vec{u} = (\vec{v},\vec{w},\vec{u}) =- (\vec{u},\vec{w},\vec{v}) = (\vec{u},\vec{v},\vec{w}) = \vec{u}\times \vec{v}\cdot \vec{w} [;\vec{u}\cdot \vec{v}\times \vec{w} = \vec{v}\times \vec{w}\cdot \vec{u} = (\vec{v},\vec{w},\vec{u}) =- (\vec{u},\vec{w},\vec{v}) = (\vec{u},\vec{v},\vec{w}) = \vec{u}\times \vec{v}\cdot \vec{w} ;]](matematica/matematica-5631d15c99756.%5Ccdot%20%5Cvec%7Bv%7D%5Ctimes%20%5Cvec%7Bw%7D%20=%20%5Cvec%7Bv%7D%5Ctimes%20%5Cvec%7Bw%7D%5Ccdot%20%5Cvec%7Bu%7D%20=%20%28%5Cvec%7Bv%7D,%5Cvec%7Bw%7D,%5Cvec%7Bu%7D%29%20=-%20%28%5Cvec%7Bu%7D,%5Cvec%7Bw%7D,%5Cvec%7Bv%7D%29%20=%20%28%5Cvec%7Bu%7D,%5Cvec%7Bv%7D,%5Cvec%7Bw%7D%29%20=%20%5Cvec%7Bu%7D%5Ctimes%20%5Cvec%7Bv%7D%5Ccdot%20%5Cvec%7Bw%7D)
![(\vec{u},\vec{v},\vec{w}) = (\vec{u},\vec{v}, \alpha \vec{u} + \beta \vec{v}) = \alpha (\vec{u},\vec{v},\vec{u}) + \beta (\vec{u},\vec{v},\vec{v}) = 0 [;(\vec{u},\vec{v},\vec{w}) = (\vec{u},\vec{v}, \alpha \vec{u} + \beta \vec{v}) = \alpha (\vec{u},\vec{v},\vec{u}) + \beta (\vec{u},\vec{v},\vec{v}) = 0;]](matematica/matematica-5631d15c18583.%20=%20%28%5Cvec%7Bu%7D,%5Cvec%7Bv%7D,%20%5Calpha%20%5Cvec%7Bu%7D%20+%20%5Cbeta%20%5Cvec%7Bv%7D%29%20=%20%5Calpha%20%28%5Cvec%7Bu%7D,%5Cvec%7Bv%7D,%5Cvec%7Bu%7D%29%20+%20%5Cbeta%20%28%5Cvec%7Bu%7D,%5Cvec%7Bv%7D,%5Cvec%7Bv%7D%29%20=%200)
devido a Prop. 2.
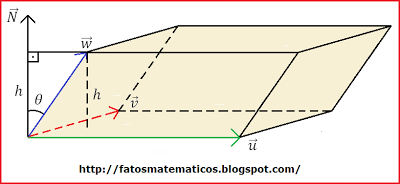
Demonstração: Na figura acima, vemos que:
![V = Sh = \mid \vec{u}\times \vec{v}\mid h \qquad (2) [;V = Sh = \mid \vec{u}\times \vec{v}\mid h \qquad (2);]](matematica/matematica-5631d160c6d21.) Mas;
Mas;
![\cos \theta = \frac{h}{\mid\vec{w}\mid} \quad \Rightarrow \quad h = \mid \vec{w}\mid \cos \theta \qquad (3) [;\cos \theta = \frac{h}{\mid\vec{w}\mid} \quad \Rightarrow \quad h = \mid \vec{w}\mid \cos \theta \qquad (3);]](matematica/matematica-5631d160d5175.)
Substituindo![(3) [;(3);]](matematica/matematica-5631d160e42b9.) em
em ![(2) [;(2);]](matematica/matematica-5631d160f26d0.) , temos:
, temos:
![V = \mid \vec{u}\times \vec{v} \mid \mid \vec{w}\mid \cos \theta = \mid \vec{u}\times \vec{v}\cdot \vec{w}\mid = \mid (\vec{u},\vec{v},\vec{w})\mid [;V = \mid \vec{u}\times \vec{v} \mid \mid \vec{w}\mid \cos \theta = \mid \vec{u}\times \vec{v}\cdot \vec{w}\mid = \mid (\vec{u},\vec{v},\vec{w})\mid;]](matematica/matematica-5631d161136ca.)
![V = \frac{\mid (\vec{u},\vec{v},\vec{w})\mid}{6} [;V = \frac{\mid (\vec{u},\vec{v},\vec{w})\mid}{6};]](matematica/matematica-5631d161546fd.)
![V =\frac{\mid (\vec{OA}, \vec{OB}, \vec{OC})\mid}{6} [;V =\frac{\mid (\vec{OA}, \vec{OB}, \vec{OC})\mid}{6};]](matematica/matematica-5631d161ab65d.)
![(\vec{OA}, \vec{OB}, \vec{OC}) =\begin{vmatrix} a & a & 0\\ 0 & a & a \\ a & 0 & a \\ \end{bmatrix} = 2a^3 [;(\vec{OA}, \vec{OB}, \vec{OC}) =\begin{vmatrix} a & a & 0\\ 0 & a & a \\ a & 0 & a \\ \end{bmatrix} = 2a^3;]](http://thewe.net/tex/%28%5Cvec%7BOA%7D,%20%5Cvec%7BOB%7D,%20%5Cvec%7BOC%7D%29%20=%5Cbegin%7Bvmatrix%7D%20a%20&%20a%20&%200%5C%5C%200%20&%20a%20&%20a%20%5C%5C%20a%20&%200%20&%20a%20%5C%5C%20%5Cend%7Bbmatrix%7D%20=%202a%5E3) segue que;
segue que;
![V = \frac{2a^3}{6} =\frac{a^3}{3} [;V = \frac{2a^3}{6} =\frac{a^3}{3};]](matematica/matematica-5631d161d028b.)
- Sobre O Produto Escalar
Por: Prof. Paulo Sérgio, Blog Fatos Matemáticos O Produto Escalar dos vetores e , denotado por é definido por: Segue desta definição que . Além disso, se é o ângulo entre dois vetores e...
- Uma Demonstração Da Desigualdade De Schwarz (em Espaços Reais)
Hermann Amandus Schwarz (1843-1921) O objetivo desta postagem é apresentar uma demonstração da desigualdade de Schwarz (não confundir com Schwartz), que enuncia o seguinte: Se $$u$$ e $$v$$ são elementos de um espaço vetorial real com produto...
- Teorema De Pitágoras Para Além Do Plano
Supomos o leitor familiarizado com as noções de espaço vetorial real e de produto interno. O objetivo desta postagem é apresentar uma versão do Teorema de Pitágoras do ponto de vista da álgebra linear, de acordo com a qual, em todo espaço vetorial...
- Cálculo Vetorial
1 - O VETORConsidere o segmento orientado AB na figura abaixo. Observe que o segmento orientado AB é caracterizado por três aspectos bastante definidos: comprimento (denominado módulo)direçãosentido (de A para B)Chama-se vetor ao conjunto infinito...
- Número Misto
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
Matemática
Sobre o Produto Misto

O Produto Misto tem seu destaque na Álgebra Vetorial devido a sua interpretação geométrica que está relacionado ao volume de paralelepípedo ou tetraedro determinado por ![3 [;3;]](matematica/matematica-5631d15bc888e.) vetores. Neste post, veremos a sua definição, suas propriedades e aplicações.
vetores. Neste post, veremos a sua definição, suas propriedades e aplicações.
Definição 1: Sejam os vetores ![\vec{u}=(x_1,y_1,z_1) [;\vec{u}=(x_1,y_1,z_1);]](matematica/matematica-5631d15bd7b83.) ,
, ![\vec{v} = (x_2,y_2,z_2) [;\vec{v} = (x_2,y_2,z_2);]](matematica/matematica-5631d15be7d1a.) e
e ![\vec{w} = (x_3,y_3,z_3) [;\vec{w} = (x_3,y_3,z_3);]](matematica/matematica-5631d15c028ad.) . O produto misto desses vetores, tomados nesta ordem e denotado por
. O produto misto desses vetores, tomados nesta ordem e denotado por ![(\vec{u},\vec{v},\vec{w}) [;(\vec{u},\vec{v},\vec{w});]](matematica/matematica-5631d15c18583.) é definido por:
é definido por:
Sendo:
segue que:
Ou seja, o produto misto dos vetores ![\vec{u} [;\vec{u};]](matematica/matematica-5631d15c99756.) ,
, ![\vec{v} [;\vec{v};]](matematica/matematica-5631d15ca8c0b.) e
e ![\vec{w} [;\vec{w};]](matematica/matematica-5631d15cb6f1a.) é um determinante de ordem
é um determinante de ordem ![3 [;3;]](matematica/matematica-5631d15bc888e.) e desta forma, suas propriedades decorrem das propriedades dos determinantes. É importante observar que o produto misto é um número real.
e desta forma, suas propriedades decorrem das propriedades dos determinantes. É importante observar que o produto misto é um número real.
Exemplo 1: Calcule
Resolução: Pela definição acima, temos;
Proposição 1: Haverá uma troca de sinal no produto misto se fizermos uma permutação entre dois vetores quaisquer, isto é,
Demonstração: Segue diretamente do fato que a purmutação entre duas linhas de um determinante, altera o seu sinal.
Proposição 2: Valem as seguintes propriedades operatórias para o produto misto.
i)
ii)
iii) Se dois vetores quaisquer são paralelos, então o produto misto é nulo, isto é;
Demonstração: Segue imediatamente das propriedades de determinantes.
Proposição 3: A permutação das operações "![\times [;\times;]](matematica/matematica-5631d15d78123.) " e "
" e "![\cdot [;\cdot;]](matematica/matematica-5631d15d86401.) " no produto misto não alteral o seu valor, isto é;
" no produto misto não alteral o seu valor, isto é;
Onde usamos a propriedade comutativa do produto escalar e a Prop. 1.
Sabemos que ![3 [;3;]](matematica/matematica-5631d15bc888e.) pontos não colineares sempre determina um único plano, mas
pontos não colineares sempre determina um único plano, mas ![4 [;4;]](matematica/matematica-5631d15dd4b59.) pontos no espaço nem sempre são coplanares. Na proposição seguinte, veremos a condição para que isto ocorra.
pontos no espaço nem sempre são coplanares. Na proposição seguinte, veremos a condição para que isto ocorra.
Proposição 4: Os pontos ![A(x_1,y_1,z_1) [;A(x_1,y_1,z_1);]](matematica/matematica-5631d15de3943.) ,
, ![B(x_2,y_2,z_2) [;B(x_2,y_2,z_2);]](matematica/matematica-5631d15e04d95.) ,
, ![C(x_3,y_3,z_3) [;C(x_3,y_3,z_3);]](matematica/matematica-5631d15e132f7.) e
e ![D(x_4,y_4,z_4) [;D(x_4,y_4,z_4);]](matematica/matematica-5631d15e22896.) são coplanares se e somente se
são coplanares se e somente se ![(\vec{u},\vec{v},\vec{w}) = 0 [;(\vec{u},\vec{v},\vec{w}) = 0;]](matematica/matematica-5631d15c18583.%20=%200) , onde
, onde ![\vec{u} = \vec{AB} [;\vec{u} = \vec{AB};]](matematica/matematica-5631d15c99756.%20=%20%5Cvec%7BAB%7D) ,
, ![\vec{v} = \vec{AC} [;\vec{v} = \vec{AC};]](matematica/matematica-5631d15ca8c0b.%20=%20%5Cvec%7BAC%7D) e
e ![\vec{w} = \vec{AD} [;\vec{w} = \vec{AD};]](matematica/matematica-5631d15cb6f1a.%20=%20%5Cvec%7BAD%7D) .
.
Demonstração: Suponhamos que os pontos ![A [;A;]](matematica/matematica-5631d15e73b12.) ,
, ![B [;B;]](matematica/matematica-5631d15e8206d.) ,
, ![C [;C;]](matematica/matematica-5631d15e97a1a.) e
e ![D [;D;]](matematica/matematica-5631d15ea6fbf.) sejam coplanares. Assim, os vetores
sejam coplanares. Assim, os vetores ![\vec{u} [;\vec{u};]](matematica/matematica-5631d15c99756.) ,
, ![\vec{v} [;\vec{v};]](matematica/matematica-5631d15ca8c0b.) e
e ![\vec{w} [;\vec{w};]](matematica/matematica-5631d15cb6f1a.) são coplanares, de modo que existem
são coplanares, de modo que existem ![\alpha, \beta \in \mathbb{R} [;\alpha, \beta \in \mathbb{R};]](matematica/matematica-5631d15ee31aa.) tais que
tais que ![\vec{w} = \alpha \vec{u} + \beta \vec{v} [;\vec{w} = \alpha \vec{u} + \beta \vec{v};]](matematica/matematica-5631d15cb6f1a.%20=%20%5Calpha%20%5Cvec%7Bu%7D%20+%20%5Cbeta%20%5Cvec%7Bv%7D) . Assim;
. Assim;
devido a Prop. 2.
Reciprocamente, se ![(\vec{u},\vec{v},\vec{w}) = 0 [;(\vec{u},\vec{v},\vec{w}) = 0;]](matematica/matematica-5631d15c18583.%20=%200) , então os vetores
, então os vetores ![\vec{u}\times \vec{v} [;\vec{u}\times \vec{v};]](matematica/matematica-5631d15c99756.%5Ctimes%20%5Cvec%7Bv%7D) e
e ![\vec{w} [;\vec{w};]](matematica/matematica-5631d15cb6f1a.) são ortogonais. Mas isto somente é possível se
são ortogonais. Mas isto somente é possível se ![\vec{w} [;\vec{w};]](matematica/matematica-5631d15cb6f1a.) pertencer ao plano definido por
pertencer ao plano definido por ![\vec{u} [;\vec{u};]](matematica/matematica-5631d15c99756.) e
e ![\vec{v} [;\vec{v};]](matematica/matematica-5631d15ca8c0b.) , ou seja,
, ou seja, ![\vec{u} [;\vec{u};]](matematica/matematica-5631d15c99756.) ,
, ![\vec{v} [;\vec{v};]](matematica/matematica-5631d15ca8c0b.) e
e ![\vec{w} [;\vec{w};]](matematica/matematica-5631d15cb6f1a.) são coplanares e consequentemente os pontos
são coplanares e consequentemente os pontos ![A [;A;]](matematica/matematica-5631d15e73b12.) ,
, ![B [;B;]](matematica/matematica-5631d15e8206d.) ,
, ![C [;C;]](matematica/matematica-5631d15e97a1a.) e
e ![D [;D;]](matematica/matematica-5631d15ea6fbf.) .
.
Proposição 5: (Interpretação Geométrica do Produto Misto). Sejam ![\vec{u} [;\vec{u};]](matematica/matematica-5631d15c99756.) ,
, ![\vec{v} [;\vec{v};]](matematica/matematica-5631d15ca8c0b.) e
e ![\vec{w} [;\vec{w};]](matematica/matematica-5631d15cb6f1a.) três vetores não coplanares. O módulo de
três vetores não coplanares. O módulo de ![(\vec{u},\vec{v},\vec{w}) [;(\vec{u},\vec{v},\vec{w});]](matematica/matematica-5631d15c18583.) é numericamente igual ao volume do paralelepípedo formado por esses vetores.
é numericamente igual ao volume do paralelepípedo formado por esses vetores.

Demonstração: Na figura acima, vemos que:
Substituindo
Corolário 1: O volume do tetraedro determinado pelos vetores ![\vec{u} [;\vec{u};]](matematica/matematica-5631d15c99756.) ,
, ![\vec{v} [;\vec{v};]](matematica/matematica-5631d15ca8c0b.) e
e ![\vec{w} [;\vec{w};]](matematica/matematica-5631d15cb6f1a.) é dado por:
é dado por:
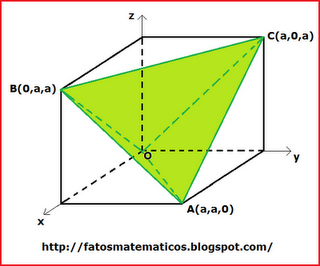
Exemplo 2: Determine o volume do tetraedro ![OABC [;OABC;]](matematica/matematica-5631d16163c47.) , na figura acima.
, na figura acima.
Resolução: Da figura, ![\vec{OA} = (a,a,0) [;\vec{OA} = (a,a,0);]](matematica/matematica-5631d16178332.) ,
, ![\vec{OB} = (0,a,a) [;\vec{OB} = (0,a,a);]](matematica/matematica-5631d1618d54b.) e
e ![\vec{OC} = (a,0,a) [;\vec{OC} = (a,0,a);]](matematica/matematica-5631d1619c256.) . Assim;
. Assim;
Sendo;
- Sobre O Produto Escalar
Por: Prof. Paulo Sérgio, Blog Fatos Matemáticos O Produto Escalar dos vetores e , denotado por é definido por: Segue desta definição que . Além disso, se é o ângulo entre dois vetores e...
- Uma Demonstração Da Desigualdade De Schwarz (em Espaços Reais)
Hermann Amandus Schwarz (1843-1921) O objetivo desta postagem é apresentar uma demonstração da desigualdade de Schwarz (não confundir com Schwartz), que enuncia o seguinte: Se $$u$$ e $$v$$ são elementos de um espaço vetorial real com produto...
- Teorema De Pitágoras Para Além Do Plano
Supomos o leitor familiarizado com as noções de espaço vetorial real e de produto interno. O objetivo desta postagem é apresentar uma versão do Teorema de Pitágoras do ponto de vista da álgebra linear, de acordo com a qual, em todo espaço vetorial...
- Cálculo Vetorial
1 - O VETORConsidere o segmento orientado AB na figura abaixo. Observe que o segmento orientado AB é caracterizado por três aspectos bastante definidos: comprimento (denominado módulo)direçãosentido (de A para B)Chama-se vetor ao conjunto infinito...
- Número Misto
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
