Matemática
Para o caso em que há três casas... vamos responder algumas perguntas:

Vamos chamar cada ponto da figura acima de vértice.
Referência:
LIPSCHUTZ, Seymour; LIPSON, Marc L. Teoria dos Grafos. In: Teoria e Problemas de Matemática Discreta. 2. ed. Porto Alegre: Bookman, 2004. (p.188-228)
*Qualquer crítica ao conteúdo apresentado pode ser feita aqui.
- Seção De Problemas - 8ª Edição
Hoje vamos ter nossa seção de problemas de número 8. Chegamos até aqui com muitos problemas já propostos, com níveis de dificuldade crescente e, em maioria, interessantíssimos. Nesta edição, não vai ser diferente: problemas extremamente interessantes,...
- Um Problema, Várias Soluções
O objetivo desta postagem é apresentar um problema muito interessante no que diz respeito à variedade de soluções possíveis. O enunciado do problema é o seguinte: Tome muitas varetas, tais quais a representada na figura 1, e comece a construir...
- Solucionando O Problema Das 3 Casas Através Da Teoria Do Grafos - Parte 1
[veja o problema aqui] Este texto é uma introdução à solução que apresentaremos para o problema das três casas. O que é um grafo? Um grafo é um conjunto de pontos com linhas contínuas (retas ou não) que unem alguns desses pares de pontos....
- O Problema Das 3 Casas
Em geral, as casas possuem uma rede de água, uma de eletricidade e uma de esgoto. Consideremos uma situação hipotética (e absurda!) que nos fornece um problema matemático dos mais curiosos: Supõe a existência de 1 casa. Esta casa,...
- Relação De Euler
A relação criada pelo matemático suíço Leonhard Euler possui extrema importância na determinação do número de arestas, vértices e faces de qualquer poliedro convexo e alguns não convexos. Essa relação permite que os cálculos sejam realizados...
Matemática
Solucionando o problema das 3 casas através da Teoria do Grafos - Parte 2
[veja o problema aqui]
[veja a 1ª parte da solução aqui]
Vamos então à solução. O texto dizia: ...deixamos os seguintes desafios para o leitor interessado e curioso: Achar a solução para o caso de duas casas ... Achar a solução para o caso de três casas ... Como responder os desafios????
Para o caso em que temos apenas duas casas, basta algumas poucas tentativas (ou uma única) para conseguirmos desenhar a figura, uma solução é a seguinte:

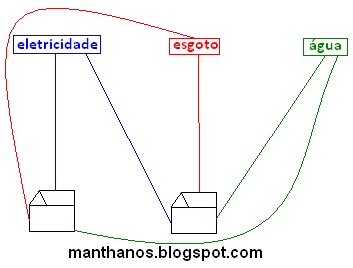
Pergunta 1: quantas ligações teriam que existir para o problema ser resolvido?

Veja que a eletricidade tem que se conectar com as 3 casas (são 3 ligações).
A água também tem que se conectar com as 3 casas (mais 3 ligações).
E de igual modo o esgoto tem que se conectar com as 3 casas (mais 3 ligações).
Portanto terá que existir 9 ligações, ou seja, nove riscos no papel.
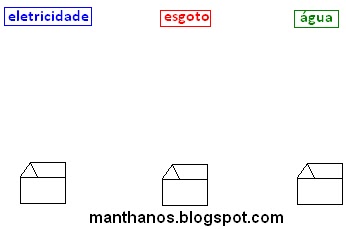
Antes de continuar vamos simplificar nossa figura e adaptar nossa linguagem de acordo com a teoria dos grafos.
Comecemos desenhando apenas pontos em vez retângulos e de casinhas:

Em vez de dizermos ligação de água (ou de esgoto ou de eletricidade) vamos simplesmente dizer arestas.
E em vez de dizermos ?figura? ou ?desenho? vamos dizer grafo.
Então nosso problema pode ser enunciado da seguinte maneira: Construir um grafo que tem 6 vértices e 9 arestas, no qual as arestas não se intersectem (ou não se cortem, ou não se cruzem, ou não passem uma por cima da outra...).
Para expressar esse fato (de as arestas não se cortarem) vamos dizer que o grafo deverá ser planar, portanto temos simplesmente que construir um grafo planar que tem 6 vértices e 9 arestas.
Note ainda, e isso é importante, que nosso grafo deverá ser conexo, ou seja, colocando uma formiga em qualquer um dos 6 vértices e dando-lhe a ordem de caminhar somente sobre as 9 arestas ela poderá perfeitamente chegar em qualquer um dos outros 5 vértices.
Pergunta 2: quantas regiões o nosso grafo deverá ter?
Para responder a esta questão, é necessário usar o Teorema de Euler (lê-se óiler) que prova-se ser válido para grafos planares conexos: V+R=A+2, onde V é o número de vértices, A é o número de arestas e R é o número de regiões.
Portanto, pelo teorema de Euler (lê-se óiler) podemos garantir que nosso grafo deverá ter 5 regiões:
V+R=A+2
6+R=9+2
6+R=11
R=11-6
R=5
Pergunta 3: no grafo que pretendemos construir, de todas as 5 regiões, qual será o grau daquela que tiver o menor grau?
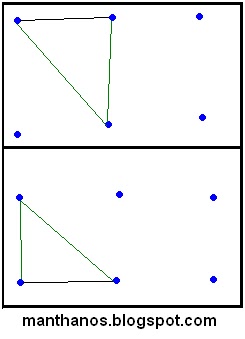
Observe que nenhuma das três casas se ligará a outra casa e nenhuma das três distribuidoras (de água, eletricidade ou esgoto) se ligará a outra distribuidora, ou seja, não haverá três vértices conectados entre si, logo não haverá este tipo de ligações (traçada em preto):

Em outras palavras: não haverá região triangular , logo o menor grau de uma das 5 regiões deverá ser 4 (maior do que 3).
Importante: note que em qualquer grafo planar conexo cada aresta é bordo (ou seja, é uma divisa) de exatamente duas regiões. Isso significa que se você somar os graus das regiões cada aresta será contada duas vezes (pois faz parte de duas regiões). Escrevendo isso como uma equação: SG=2A, onde SG é a soma dos graus e A é o número de arestas.
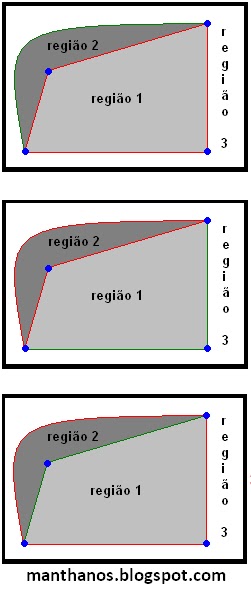
Vejamos um exemplo de um caso particular para compreendermos melhor o que acaba de ser dito:

No grafo acima (que foi desenhado três vezes com destaque em vermelho ao bordo de cada região) observamos que:
O grau da região 1 é 4.
O grau da região 2 é 3.
O grau da região 3 é 3.
Somando os graus das três regiões obtemos 4+3+3=10. Note que o grafo possui 5 arestas, então neste grafo, assim como em qualquer outro que seja planar conexo, a soma dos graus (10) é igual ao dobro (2 vezes) do número de arestas (5): 10=2.5.
Usando estas informações podemos chegar a uma conclusão: propomos que o leitor que desconhece a resposta medite nas informações apresentadas acima para tentar elaborar um argumento que responde ao desafio para o caso em que há três casas. E só então leia a parte final.
- Seção De Problemas - 8ª Edição
Hoje vamos ter nossa seção de problemas de número 8. Chegamos até aqui com muitos problemas já propostos, com níveis de dificuldade crescente e, em maioria, interessantíssimos. Nesta edição, não vai ser diferente: problemas extremamente interessantes,...
- Um Problema, Várias Soluções
O objetivo desta postagem é apresentar um problema muito interessante no que diz respeito à variedade de soluções possíveis. O enunciado do problema é o seguinte: Tome muitas varetas, tais quais a representada na figura 1, e comece a construir...
- Solucionando O Problema Das 3 Casas Através Da Teoria Do Grafos - Parte 1
[veja o problema aqui] Este texto é uma introdução à solução que apresentaremos para o problema das três casas. O que é um grafo? Um grafo é um conjunto de pontos com linhas contínuas (retas ou não) que unem alguns desses pares de pontos....
- O Problema Das 3 Casas
Em geral, as casas possuem uma rede de água, uma de eletricidade e uma de esgoto. Consideremos uma situação hipotética (e absurda!) que nos fornece um problema matemático dos mais curiosos: Supõe a existência de 1 casa. Esta casa,...
- Relação De Euler
A relação criada pelo matemático suíço Leonhard Euler possui extrema importância na determinação do número de arestas, vértices e faces de qualquer poliedro convexo e alguns não convexos. Essa relação permite que os cálculos sejam realizados...
