Matemática
Os primeiros registros encontrados sobre a resolução de algumas equações de segundo grau são de aproximadamente $1700a.C.$ e pertence à civilizações antigas dos sumérios, egípcios e babilônios.
Os gregos aperfeiçoaram a técnica de resolução de equações de segundo grau utilizando a Geometria.
A obra Al-jabr W'al-Magabala do matemático e astrônomo Al-Kowarizmi, datada do século $VIII$ inclui resoluções completas de equações de $1º$ e $2º$ graus. A palavra "álgebra" surge daí.
No século $XVI$ com o Renascimento italiano, houve um progresso na Álgebra: a resolução de equações de $3º$ e $4º$ graus. A história da resolução dessas equações envolvem segredos, desafios e traições, culminando em $1545$ com a publicação de Ars Magna, de Girolamo Cardano, contendo o processo de resolução e a devida demonstração da fórmula da resolução de uma equação de terceiro grau, além de explicar como se resolver uma equação de quarto grau.
Durante dois séculos e meio, tentou-se encontrar uma fórmula para a resolução de equações de $5º$, mas somente em $1824$ o matemático norueguês Niels Abel $(1802-1829)$ provou consistentemente a impossibilidade de resolução dessas equações por meio das quatro operações básicas aritméticas e de radiciações.
Logo depois, Evariste Galois $(1811-1832)$ generalizou as condições de resolubilidade de uma equação algébrica qualquer, dando origem à Álgebra Moderna.
A demonstração desse teorema foi a tese de doutoramento do grande Gauss $(1777-1855)$, então com $21$ anos, constituindo um elemento central para o estudo das equações algébricas.

\begin{equation}
P(x) \equiv a_nx^n + a_{n-1}x^{n-1} + \cdots +a_1x + a_0
\end{equation}
pode ser fatorado como o produto de uma constante por polinômios de primeiro grau:
\begin{equation}
P(x) \equiv a_n(x-r_1)(x-r_2)\cdots (x-r_n)
\end{equation}
onde $r_1, r_2, \cdots , r_n$ são todas as raízes de $P(x)$.
\begin{equation}
P(x) \equiv a_nx^n + a_{n-1}x^{n-1} + \cdots +a_1x + a_0
\end{equation}
Pelo Teorema fundamental da Álgebra (TFA) , $P(x)$ admite uma raiz complexa $r_1$. Logo, podemos escrever $P(x)$ como:
\begin{equation}
P(x) \equiv (x-r_1) \cdot Q_1(x)
\end{equation}
onde $Q_1(x)$ tem grau $n-1$.
Se $n-1 \geq 1$, então pelo TFA, $Q_1(x)$ admite uma raiz complexa $r_2$ e podemos escrever:
\begin{equation}
Q_1(x) \equiv (x-r_2)\cdot Q_2(x)
\end{equation}
Substituindo $(5)$ em $(4)$, obtemos:
\begin{equation}
P(x) \equiv (x-r_1)(x-r_2)\cdot Q_2(x)
\end{equation}
Repetindo esse processo até que $Q_n(x)$ seja constante, obtemos:
\begin{equation}
P(x) \equiv (x-r_1)(x-r_2)(x-r_3)\cdots (x-r_n)\cdot Q_n(x)
\end{equation}
Por definição de identidade de polinômios, temos que o coeficiente $a_n$ de $P(x)$ deve ser igual a $Q_n(x)$. Logo:
\begin{equation}
P(x) \equiv a_n(x-r_1)(x-r_2)(x-r_3)\cdots (x-r_n)
\end{equation}
Primeiramente devemos encontrar as raízes do polinômio. Para isso, igualamos a zero e assim poderemos aplicar a fórmula para a equação de segundo grau:
\begin{equation*}
2x^2-7x+3=0\\
x=\frac{7\pm\sqrt{(-7)^2-4\cdot2\cdot3}}{4}\\
x=\frac{7\pm 5}{4}\\
x_1=\frac{7+5}{4}=3\\
x_2=\frac{7-5}{4}=\frac{1}{2}
\end{equation*}
Agora, pelo Teorema da Decomposição, temos:
\begin{equation*}
P(x) \equiv 2(x-3)(x-1/2)
\end{equation*}
$2)$ Decompor $P(x) \equiv 4x^2-x-3$ como o produto de uma constante por polinômios de primeiro grau.
Fazemos:
\begin{equation*}
4x^2-x-3=0\\
x=\frac{1\pm\sqrt{(-1)^2-4\cdot 4\cdot(-3)}}{8}\\
x_1=\frac{1+7}{8}=1\\
x_2=\frac{1-7}{8}=-\frac{3}{4}
\end{equation*}
Assim pelo Teorema da Decomposição:
\begin{equation*}
P(x)\equiv 4(x-1)(x+3/4)
\end{equation*}
$3)$ Decompor $P(x) \equiv x^3-8x^2 +12x$ como o produto de uma constante por polinômios de primeiro grau.
Fazemos:
\begin{equation*}
x^3-8x^2+12x=0\\
x(x^2-8x+12)=0
\end{equation*}
Então, temos que $x=0$ ou $x^2-8x+12=0$. Aplicando a fórmula para a equação de segundo grau:
\begin{equation*}
x^2-8x+12=0\\
x=\frac{8\pm \sqrt{(-8)^2-4\cdot 12}}{2}\\
x=\frac{8\pm 4}{2}\\
x_1=6\\
x_2=2
\end{equation*}
Assim, pelo Teorema da Decomposição:
\begin{equation*}
P(x)\equiv 1(x-0)(x-6)(x-2)\\
P(x) \equiv (x-2)(x-6)
\end{equation*}
$4)$ Uma das raízes do polinômio $P(x) \equiv 3x^3-20x^2+23x+10$ é $5$. Fatorar $P(x)$ como o produto de uma constante por polinômios de primeiro grau.
Como $5$ é uma raiz de $P(x)$, pelo Teorema de D'Alembert, temos que $P(x)$ é divisível por $(x-5)$, ou seja $P(x) \equiv (x-5)\cdot Q(x)$. Obtemos $Q(x)$ dividindo $P(x)$ por $(x-5)$. Assim, podemos aplicar Briot-Ruffini para encontrarmos as outras raízes:
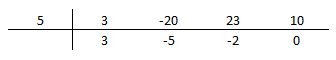
Logo, $Q(x) \equiv 3x^2-5x-2$. Portanto, $P(x) \equiv (x-5)(3x^2-5x-2)$.
As raízes de $P(x)$ são dadas por: $(x-5)(3x^2-5x-2)=0$. Então, ou $x-5=0$ ou $3x^2-5x-2=0$. Para $x-5=0$, temos que $x=5$. Aplicando a fórmula da equação de segundo grau na segunda equação, encontramos como raízes $2$ e $-1/3$. Assim, pelo Teorema da Decomposição:
\begin{equation*}
P(x) \equiv 3(x-5)(x-2)(x+1/3)
\end{equation*}
$5)$ Sabendo que $3$ é uma raiz dupla da equação $x^4-12x^3+53x^2-102x+72=0$, obter as outras raízes em $\mathbb{C}$.
Pelo Teorema da Decomposição, a equação pode ser reescrita como:
\begin{equation*}
(x-3)\underbrace{(x-3)\overbrace{(x-r_3)(x-r_4)}^{Q_2(x)}}_{Q_1(x)}=0
\end{equation*}
onde $r_3$ e $r_4$ são outras duas raízes da equação, além do $3$.
Dividindo $P(x)\equiv x^4-12x^3+53x^2 -102x +72$ por $x-3$, obtemos $Q_1(x)$. E dividindo $Q_1(x)$ por $x-3$, obtemos $Q_2(x)$. Aplicando Briot-Ruffini:
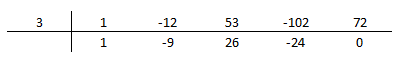
Portanto, $Q_1(x) \equiv x^3-9x^2+26x-24$. Para $Q_2(x)$, fazemos:
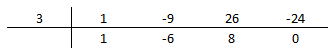
Portanto, $Q_2(x) \equiv x^2-6x+8$.
Agora, reescrevemos a equação original como:
\begin{equation*}
(x-3)(x-3)(x^2-6x+8)=0
\end{equation*}
Resolvendo cada uma das equações:
\begin{equation*}
x-3=0\\
x=3
\end{equation*}
e
\begin{equation*}
x^2-6x+8=0\\
x_1=4\\
x_2=2
\end{equation*}
Portanto, além da raiz dupla $r_1=r_2=3$, a equação admite outras duas raízes iguais a $r_3=2$ e $r_4=4$.
➋ Multiplicidade de uma Raiz
➌ Dispositivo Prático de Briot-Ruffini

- Resolução Da Integral $\int \frac{1}{a\ E^{bx}}dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{a\ e^{bx}}dx = -\frac{e^{-bx}}{ab}+C \end{equation*} onde $a$ e $b \in \mathbb{R}$ e $a$ e $b \neq 0$. Seja a integral: \begin{equation*} I = \int \frac{1}{a\ e^{bx}}dx = \int \frac{e^{-bx}}{a}...
- Integral Indefinida Do Produto De Cossenos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation} \int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}...
- Integral Indefinida Do Produto De Senos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois senos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation*} \int \text{sen}(ax) \cdot \text{sen}(bx)\ dx=\frac{\text{sen} [(a-b) x]}{2 (a-b)}...
- Prova Do Teorema De Pitágoras, Baseado Nas Relações Métricas Da Circunferência
Esta demonstração do teorema de Pitágoras, baseia-se nas relações métricas da circunferência. Considere o triângulo $ABC$. Tomando como centro o ponto $B$ e raio igual a hipotenusa $AB$, traçamos uma circunferência. A seguir prolongamos os...
- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...
Matemática
Teorema da Decomposição de Polinômios
Os primeiros registros encontrados sobre a resolução de algumas equações de segundo grau são de aproximadamente $1700a.C.$ e pertence à civilizações antigas dos sumérios, egípcios e babilônios.
Os gregos aperfeiçoaram a técnica de resolução de equações de segundo grau utilizando a Geometria.
A obra Al-jabr W'al-Magabala do matemático e astrônomo Al-Kowarizmi, datada do século $VIII$ inclui resoluções completas de equações de $1º$ e $2º$ graus. A palavra "álgebra" surge daí.
No século $XVI$ com o Renascimento italiano, houve um progresso na Álgebra: a resolução de equações de $3º$ e $4º$ graus. A história da resolução dessas equações envolvem segredos, desafios e traições, culminando em $1545$ com a publicação de Ars Magna, de Girolamo Cardano, contendo o processo de resolução e a devida demonstração da fórmula da resolução de uma equação de terceiro grau, além de explicar como se resolver uma equação de quarto grau.
Durante dois séculos e meio, tentou-se encontrar uma fórmula para a resolução de equações de $5º$, mas somente em $1824$ o matemático norueguês Niels Abel $(1802-1829)$ provou consistentemente a impossibilidade de resolução dessas equações por meio das quatro operações básicas aritméticas e de radiciações.
Logo depois, Evariste Galois $(1811-1832)$ generalizou as condições de resolubilidade de uma equação algébrica qualquer, dando origem à Álgebra Moderna.
Teorema Fundamental da Álgebra
O Teorema Fundamental da Álgebra (TFA) nos garante que todo polinômio $p(x)=0$ de grau $n$, $n \geq 1$, admite pelo menos uma raiz complexa, real ou não.A demonstração desse teorema foi a tese de doutoramento do grande Gauss $(1777-1855)$, então com $21$ anos, constituindo um elemento central para o estudo das equações algébricas.
Teorema da Decomposição em Fatores de Primeiro Grau
Uma consequência do Teorema fundamental da Álgebra é o Teorema da Decomposição.
Teorema:
Todo polinômio $P(x)$ de grau $n \geq 1$:\begin{equation}
P(x) \equiv a_nx^n + a_{n-1}x^{n-1} + \cdots +a_1x + a_0
\end{equation}
pode ser fatorado como o produto de uma constante por polinômios de primeiro grau:
\begin{equation}
P(x) \equiv a_n(x-r_1)(x-r_2)\cdots (x-r_n)
\end{equation}
onde $r_1, r_2, \cdots , r_n$ são todas as raízes de $P(x)$.
Demonstração:
Seja $P(x)$ um polinômio de grau $n \geq 1$:\begin{equation}
P(x) \equiv a_nx^n + a_{n-1}x^{n-1} + \cdots +a_1x + a_0
\end{equation}
Pelo Teorema fundamental da Álgebra (TFA) , $P(x)$ admite uma raiz complexa $r_1$. Logo, podemos escrever $P(x)$ como:
\begin{equation}
P(x) \equiv (x-r_1) \cdot Q_1(x)
\end{equation}
onde $Q_1(x)$ tem grau $n-1$.
Se $n-1 \geq 1$, então pelo TFA, $Q_1(x)$ admite uma raiz complexa $r_2$ e podemos escrever:
\begin{equation}
Q_1(x) \equiv (x-r_2)\cdot Q_2(x)
\end{equation}
Substituindo $(5)$ em $(4)$, obtemos:
\begin{equation}
P(x) \equiv (x-r_1)(x-r_2)\cdot Q_2(x)
\end{equation}
Repetindo esse processo até que $Q_n(x)$ seja constante, obtemos:
\begin{equation}
P(x) \equiv (x-r_1)(x-r_2)(x-r_3)\cdots (x-r_n)\cdot Q_n(x)
\end{equation}
Por definição de identidade de polinômios, temos que o coeficiente $a_n$ de $P(x)$ deve ser igual a $Q_n(x)$. Logo:
\begin{equation}
P(x) \equiv a_n(x-r_1)(x-r_2)(x-r_3)\cdots (x-r_n)
\end{equation}
Exemplos:
$1)$ Fatorar o polinômio $P(x) \equiv 2x^2-7x+3$ como o produto de uma constante por polinômios de primeiro grau.Primeiramente devemos encontrar as raízes do polinômio. Para isso, igualamos a zero e assim poderemos aplicar a fórmula para a equação de segundo grau:
\begin{equation*}
2x^2-7x+3=0\\
x=\frac{7\pm\sqrt{(-7)^2-4\cdot2\cdot3}}{4}\\
x=\frac{7\pm 5}{4}\\
x_1=\frac{7+5}{4}=3\\
x_2=\frac{7-5}{4}=\frac{1}{2}
\end{equation*}
Agora, pelo Teorema da Decomposição, temos:
\begin{equation*}
P(x) \equiv 2(x-3)(x-1/2)
\end{equation*}
$2)$ Decompor $P(x) \equiv 4x^2-x-3$ como o produto de uma constante por polinômios de primeiro grau.
Fazemos:
\begin{equation*}
4x^2-x-3=0\\
x=\frac{1\pm\sqrt{(-1)^2-4\cdot 4\cdot(-3)}}{8}\\
x_1=\frac{1+7}{8}=1\\
x_2=\frac{1-7}{8}=-\frac{3}{4}
\end{equation*}
Assim pelo Teorema da Decomposição:
\begin{equation*}
P(x)\equiv 4(x-1)(x+3/4)
\end{equation*}
$3)$ Decompor $P(x) \equiv x^3-8x^2 +12x$ como o produto de uma constante por polinômios de primeiro grau.
Fazemos:
\begin{equation*}
x^3-8x^2+12x=0\\
x(x^2-8x+12)=0
\end{equation*}
Então, temos que $x=0$ ou $x^2-8x+12=0$. Aplicando a fórmula para a equação de segundo grau:
\begin{equation*}
x^2-8x+12=0\\
x=\frac{8\pm \sqrt{(-8)^2-4\cdot 12}}{2}\\
x=\frac{8\pm 4}{2}\\
x_1=6\\
x_2=2
\end{equation*}
Assim, pelo Teorema da Decomposição:
\begin{equation*}
P(x)\equiv 1(x-0)(x-6)(x-2)\\
P(x) \equiv (x-2)(x-6)
\end{equation*}
$4)$ Uma das raízes do polinômio $P(x) \equiv 3x^3-20x^2+23x+10$ é $5$. Fatorar $P(x)$ como o produto de uma constante por polinômios de primeiro grau.
Como $5$ é uma raiz de $P(x)$, pelo Teorema de D'Alembert, temos que $P(x)$ é divisível por $(x-5)$, ou seja $P(x) \equiv (x-5)\cdot Q(x)$. Obtemos $Q(x)$ dividindo $P(x)$ por $(x-5)$. Assim, podemos aplicar Briot-Ruffini para encontrarmos as outras raízes:
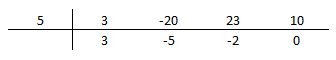
Logo, $Q(x) \equiv 3x^2-5x-2$. Portanto, $P(x) \equiv (x-5)(3x^2-5x-2)$.
As raízes de $P(x)$ são dadas por: $(x-5)(3x^2-5x-2)=0$. Então, ou $x-5=0$ ou $3x^2-5x-2=0$. Para $x-5=0$, temos que $x=5$. Aplicando a fórmula da equação de segundo grau na segunda equação, encontramos como raízes $2$ e $-1/3$. Assim, pelo Teorema da Decomposição:
\begin{equation*}
P(x) \equiv 3(x-5)(x-2)(x+1/3)
\end{equation*}
$5)$ Sabendo que $3$ é uma raiz dupla da equação $x^4-12x^3+53x^2-102x+72=0$, obter as outras raízes em $\mathbb{C}$.
Pelo Teorema da Decomposição, a equação pode ser reescrita como:
\begin{equation*}
(x-3)\underbrace{(x-3)\overbrace{(x-r_3)(x-r_4)}^{Q_2(x)}}_{Q_1(x)}=0
\end{equation*}
onde $r_3$ e $r_4$ são outras duas raízes da equação, além do $3$.
Dividindo $P(x)\equiv x^4-12x^3+53x^2 -102x +72$ por $x-3$, obtemos $Q_1(x)$. E dividindo $Q_1(x)$ por $x-3$, obtemos $Q_2(x)$. Aplicando Briot-Ruffini:
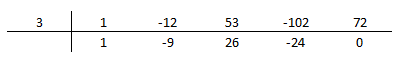
Portanto, $Q_1(x) \equiv x^3-9x^2+26x-24$. Para $Q_2(x)$, fazemos:
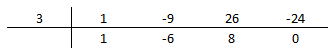
Portanto, $Q_2(x) \equiv x^2-6x+8$.
Agora, reescrevemos a equação original como:
\begin{equation*}
(x-3)(x-3)(x^2-6x+8)=0
\end{equation*}
Resolvendo cada uma das equações:
\begin{equation*}
x-3=0\\
x=3
\end{equation*}
e
\begin{equation*}
x^2-6x+8=0\\
x_1=4\\
x_2=2
\end{equation*}
Portanto, além da raiz dupla $r_1=r_2=3$, a equação admite outras duas raízes iguais a $r_3=2$ e $r_4=4$.
Referências:
[1] Matemática Volume Único - Manoel Paiva - Ed. ModernaVeja mais:
➊ Divisão de Polinômios➋ Multiplicidade de uma Raiz
➌ Dispositivo Prático de Briot-Ruffini

- Resolução Da Integral $\int \frac{1}{a\ E^{bx}}dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{a\ e^{bx}}dx = -\frac{e^{-bx}}{ab}+C \end{equation*} onde $a$ e $b \in \mathbb{R}$ e $a$ e $b \neq 0$. Seja a integral: \begin{equation*} I = \int \frac{1}{a\ e^{bx}}dx = \int \frac{e^{-bx}}{a}...
- Integral Indefinida Do Produto De Cossenos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation} \int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}...
- Integral Indefinida Do Produto De Senos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois senos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation*} \int \text{sen}(ax) \cdot \text{sen}(bx)\ dx=\frac{\text{sen} [(a-b) x]}{2 (a-b)}...
- Prova Do Teorema De Pitágoras, Baseado Nas Relações Métricas Da Circunferência
Esta demonstração do teorema de Pitágoras, baseia-se nas relações métricas da circunferência. Considere o triângulo $ABC$. Tomando como centro o ponto $B$ e raio igual a hipotenusa $AB$, traçamos uma circunferência. A seguir prolongamos os...
- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...
