Matemática
Olá gente! Hoje aprensentarei um problema bastante conhecido em geometria e algumas de suas soluções também muito conhecidas.
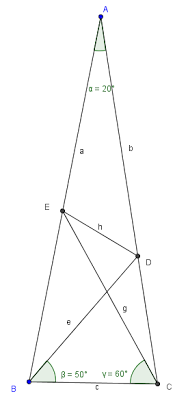
O triângulo![ABC [;ABC;]](matematica/matematica-5631c8bf2dd81.) ao lado é isósceles de vértice
ao lado é isósceles de vértice ![A=20^{\circ} [;A=20^{\circ};]](matematica/matematica-5631c8bf3cc07.) .
.
Sendo![D\hat{B}C=50^{\circ} [;D\hat{B}C=50^{\circ};]](matematica/matematica-5631c8bf4c421.) e
e ![E\hat{C}B=60^{\circ} [;E\hat{C}B=60^{\circ};]](matematica/matematica-5631c8bf5b038.) calcule
calcule ![C\hat{E}D [;C\hat{E}D;]](matematica/matematica-5631c8bf70a6b.) .
.
Resolução 1 :
Vamos usar lei dos senos nessa solução. Clique aqui para ler o post do João sobre geometria com contas.
Se fizermos![C\hat{E}D=x [;C\hat{E}D=x;]](matematica/matematica-5631c8bf70a6b.=x) então
então ![C\hat{D}E=160^{\circ} -x [;C\hat{D}E=160^{\circ} -x;]](matematica/matematica-5631c8bf8eb9d.)
Aplicando a Lei dos Senos no triângulo![CDE [;CDE;]](matematica/matematica-5631c8bf9e2b6.) ...
...
![\frac{CE}{CD}= [;\frac{CE}{CD}=;]](matematica/matematica-5631c8bfb3e3a.)
![\frac{sen(160^{\circ}-x)}{sen (x)} [;\frac{sen(160^{\circ}-x)}{sen (x)};]](matematica/matematica-5631c8bfc2d5a.) (I)
(I)
e no triângulo![BCE [;BCE;]](matematica/matematica-5631c8bfd29a7.) obtemos:
obtemos:
![\frac{CE}{BC}= \frac{sen(80^{\circ})}{sen(40^{\circ})} = 2 \cdot cos (40^{\circ}) [;\frac{CE}{BC}= \frac{sen(80^{\circ})}{sen(40^{\circ})} = 2 \cdot cos (40^{\circ});]](matematica/matematica-5631c8bfe1113.) (II) (só usar a fórmula do seno do arco duplo!)
(II) (só usar a fórmula do seno do arco duplo!)
Como![C\hat{B}D= [;C\hat{B}D=;]](matematica/matematica-5631c8c002af1.)
![C\hat{D}B [;C\hat{D}B;]](matematica/matematica-5631c8c011c4a.)
![= [;=;]](matematica/matematica-5631c8c020ee1.)
![50^{\circ} [;50^{\circ};]](matematica/matematica-5631c8c0305d9.) então
então ![\triangle{BCD} [;\triangle{BCD};]](matematica/matematica-5631c8c03f603.) é isosceles. Assim,
é isosceles. Assim, ![CD=BC [;CD=BC;]](matematica/matematica-5631c8c058cc1.)
Isso nos permite escrever (I)=(II)
Logo,![\frac{sen(160^{\circ} -x)}{sen(x)}=2 \cdot cos(40^{\circ}) [;\frac{sen(160^{\circ} -x)}{sen(x)}=2 \cdot cos(40^{\circ});]](matematica/matematica-5631c8c067eb5.)
Sendo![sen(180^{\circ} - x) = sen(x) [;sen(180^{\circ} - x) = sen(x);]](matematica/matematica-5631c8c076cf2.)
Temos
![sen(160^{\circ} - x)= [;sen(160^{\circ} - x)=;]](matematica/matematica-5631c8c0868a9.)
![sen(180^{\circ} - (160^{\circ} - x)) = [; sen(180^{\circ} - (160^{\circ} - x)) =;]](matematica/matematica-5631c8c09579b.)
![sen(20^{\circ}+ x) = 2\cdot cos(40^{\circ}) \cdot sen(x)=2\cdot cos(60^{\circ} - 20^{\circ}) \cdot sen(x) [;sen(20^{\circ}+ x) = 2\cdot cos(40^{\circ}) \cdot sen(x)=2\cdot cos(60^{\circ} - 20^{\circ}) \cdot sen(x);]](matematica/matematica-5631c8c0a4425.)
Usando a fórmula da soma de arcos para o seno e da subtração de arcos para o cosseno obtemos:
![sen(20^{\circ}) \cdot cos (x) + [;sen(20^{\circ}) \cdot cos (x) +;]](matematica/matematica-5631c8c0b34d0.)
![cos(20^{\circ}) [;cos(20^{\circ});]](matematica/matematica-5631c8c0c8329.)
![\cdot [;\cdot;]](matematica/matematica-5631c8c0ddd4f.)
![sen(x)= [; sen(x)=;]](matematica/matematica-5631c8c0ec725.)
![cos(20^{\circ}) [;cos(20^{\circ});]](matematica/matematica-5631c8c0c8329.)
![\cdot sen(x) [; \cdot sen(x);]](matematica/matematica-5631c8c11bce1.)
![+ \sqrt{3} [; + \sqrt{3};]](matematica/matematica-5631c8c12b246.)
![sen(20^{\circ}) [;sen(20^{\circ});]](matematica/matematica-5631c8c13a385.)
![\cdot sen(x) [; \cdot sen(x);]](matematica/matematica-5631c8c11bce1.)
![sen(20^{\circ}) \cdot cos(x) = \sqrt{3}sen(20^{\circ}) \cdot sen(x) [;sen(20^{\circ}) \cdot cos(x) = \sqrt{3}sen(20^{\circ}) \cdot sen(x);]](matematica/matematica-5631c8c13a385.%20%5Ccdot%20cos%28x%29%20=%20%5Csqrt%7B3%7Dsen%2820%5E%7B%5Ccirc%7D%29%20%5Ccdot%20sen%28x%29)
![ctg(x)=\sqrt{3} [;ctg(x)=\sqrt{3};]](matematica/matematica-5631c8c16ef0b.)
daonde![x=30^{\circ} [; x=30^{\circ};]](matematica/matematica-5631c8c17d518.) .
.
Uma outra solução é obtida de forma mais bonita.
Resolução 2:
Observe a construção abaixo
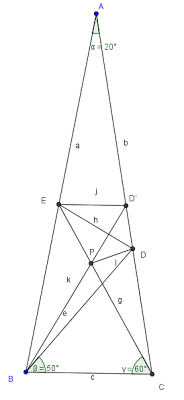
Na figura abaixo![ED'\parallel BC [;ED'\parallel BC;]](matematica/matematica-5631c8c21720d.) . Seja
. Seja ![P [;P;]](matematica/matematica-5631c8c226291.) o ponto de encontro de
o ponto de encontro de![BD' [;BD';]](matematica/matematica-5631c8c235b14.) com
com![CE [;CE;]](matematica/matematica-5631c8c245590.) . Assim,
. Assim, ![\triangle{BCP} [; \triangle{BCP};]](matematica/matematica-5631c8c253c69.) e
e ![\triangle{ED'P} [;\triangle{ED'P};]](matematica/matematica-5631c8c262ead.) são triângulos equiláteros. Ou seja,
são triângulos equiláteros. Ou seja, ![CP=BC [;CP=BC;]](matematica/matematica-5631c8c271722.) como
como ![\triangle{BCD} [;\triangle{BCD};]](matematica/matematica-5631c8c03f603.) é isosceles, então
é isosceles, então ![\triangle{PCD} [;\triangle{PCD};]](matematica/matematica-5631c8c295580.) é isosceles com ângulo do vértice
é isosceles com ângulo do vértice ![\hat{C}=20^{\circ} [;\hat{C}=20^{\circ};]](matematica/matematica-5631c8c2aafda.) , assim
, assim![C\hat{P}D=80^{\circ} [;C\hat{P}D=80^{\circ};]](matematica/matematica-5631c8c2b997b.) como
como ![E\hat{P}D'=60^{\circ} [;E\hat{P}D'=60^{\circ};]](matematica/matematica-5631c8c2c8866.) e
e ![E,P [;E,P;]](matematica/matematica-5631c8c2de481.) e
e ![C [;C;]](matematica/matematica-5631c8c2edefd.) são colineares,
são colineares, ![D'\hat{P}C=40^{\circ} [;D'\hat{P}C=40^{\circ};]](matematica/matematica-5631c8c30ecf9.) .
.
Como![D'\hat{P}C=40^{\circ} [;D'\hat{P}C=40^{\circ};]](matematica/matematica-5631c8c30ecf9.) e
e ![B\hat{D'}C=40^{\circ} [;B\hat{D'}C=40^{\circ};]](matematica/matematica-5631c8c32c63f.)
![\triangle{PDD'} [;\triangle{PDD'};]](matematica/matematica-5631c8c33b639.) é isosceles com angulo do vétice
é isosceles com angulo do vétice ![\hat{D}=100^{\circ} [; \hat{D}=100^{\circ};]](matematica/matematica-5631c8c3502f5.) .
.
Lembrando que![\triangle{EPD'} [;\triangle{EPD'};]](matematica/matematica-5631c8c35ef7d.) é equilatero. Temos
é equilatero. Temos ![ED'=EP [;ED'=EP;]](matematica/matematica-5631c8c36ea1f.) e
e ![DP=DD' [;DP=DD';]](matematica/matematica-5631c8c37d8ed.) assim, pelo caso LLL,
assim, pelo caso LLL, ![\triangle{EPD}=\triangle{EDD'} [;\triangle{EPD}=\triangle{EDD'};]](matematica/matematica-5631c8c38d180.) . Por isso,
. Por isso, ![ED [;ED;]](matematica/matematica-5631c8c3a22a2.) é bissetriz de
é bissetriz de ![P\hat{E}D' [;P\hat{E}D';]](matematica/matematica-5631c8c226291.%5Chat%7BE%7DD%27) , logo,
, logo, ![C\hat{E}D=30^{\circ} [;C\hat{E}D=30^{\circ};]](matematica/matematica-5631c8bf70a6b.=30%5E%7B%5Ccirc%7D) .
.
Há muitas outras soluções para esse problema. Por que você não tenta a sua?
Lembre-se: Para melhorar a qualidade de nossas postagens avalie-as logo abaixo. Se você gostou do blog recomende aos seus amigos e se inscreva por e-mail para receber nossas atualizações.
Até mais!
- Questão 35 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
A medida do ângulo interno de um octógono regular é (A) 45°.(B) 60°(C) 90°.(D) 120°.(E) 135°. Solução: (E) Aplicando o Método de Resolução de Problemas segundo Polya: 1° ? Compreensão do Problema O octógono regular (vide Figura 1) é o...
- Lei Dos Cossenos
Lei dos cossenosMarcelo Rigonatto TriânguloSabemos que as relações trigonométricas do seno, cosseno e tangente são válidas somente em um triângulo retângulo. Quando estamos trabalhando com triângulos quaisquer, acutângulos...
- Geométria Plana Resumo
1) Ângulos em retas paralelas 2) Triângulos # Classificação: Equilátero 3 lados iguais. Isósceles 2 lados iguais. Escaleno 3 lados desiguais. # Ângulos: A soma dos ângulos internos de um triângulo é igual a 180º. A soma dos ângulos externos...
- Lei Dos Senos E Dos Cossenos
Resolver triângulos é estabelecer um conjunto de cálculos que nos permitam determinar os lados, ângulos e outros segmentos do triângulo. A lei dos senos e dos cossenos, são utilizadas para a resolução de triângulos quaisquer. Lei dos Cossenos...
- Lei Dos Senos
Lei dos senosMarcelo Rigonatto Trigonometria no triânguloAs relações trigonométricas do seno, cosseno e tangente são válidas somente no triângulo retângulo, porém, podemos estabelecer algumas identidades trigonométricas...
Matemática
Um problema famoso de Geometria
Olá gente! Hoje aprensentarei um problema bastante conhecido em geometria e algumas de suas soluções também muito conhecidas.

O triângulo
Sendo
Resolução 1 :
Vamos usar lei dos senos nessa solução. Clique aqui para ler o post do João sobre geometria com contas.
Se fizermos
Aplicando a Lei dos Senos no triângulo
e no triângulo
Como
Isso nos permite escrever (I)=(II)
Logo,
Sendo
Temos
Usando a fórmula da soma de arcos para o seno e da subtração de arcos para o cosseno obtemos:
daonde
Uma outra solução é obtida de forma mais bonita.
Resolução 2:
Observe a construção abaixo

Na figura abaixo
Como
Lembrando que
Há muitas outras soluções para esse problema. Por que você não tenta a sua?
Lembre-se: Para melhorar a qualidade de nossas postagens avalie-as logo abaixo. Se você gostou do blog recomende aos seus amigos e se inscreva por e-mail para receber nossas atualizações.
Até mais!
- Questão 35 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
A medida do ângulo interno de um octógono regular é (A) 45°.(B) 60°(C) 90°.(D) 120°.(E) 135°. Solução: (E) Aplicando o Método de Resolução de Problemas segundo Polya: 1° ? Compreensão do Problema O octógono regular (vide Figura 1) é o...
- Lei Dos Cossenos
Lei dos cossenosMarcelo Rigonatto TriânguloSabemos que as relações trigonométricas do seno, cosseno e tangente são válidas somente em um triângulo retângulo. Quando estamos trabalhando com triângulos quaisquer, acutângulos...
- Geométria Plana Resumo
1) Ângulos em retas paralelas 2) Triângulos # Classificação: Equilátero 3 lados iguais. Isósceles 2 lados iguais. Escaleno 3 lados desiguais. # Ângulos: A soma dos ângulos internos de um triângulo é igual a 180º. A soma dos ângulos externos...
- Lei Dos Senos E Dos Cossenos
Resolver triângulos é estabelecer um conjunto de cálculos que nos permitam determinar os lados, ângulos e outros segmentos do triângulo. A lei dos senos e dos cossenos, são utilizadas para a resolução de triângulos quaisquer. Lei dos Cossenos...
- Lei Dos Senos
Lei dos senosMarcelo Rigonatto Trigonometria no triânguloAs relações trigonométricas do seno, cosseno e tangente são válidas somente no triângulo retângulo, porém, podemos estabelecer algumas identidades trigonométricas...
