Matemática
O cilindro é um sólido geométrico bastante utilizado na indústria de embalagens e na armazenagem de líquidos em geral. É considerado um corpo redondo por conter uma de suas faces arredondadas. Em razão dessa característica, o cálculo de sua área total requer algumas observações e certo cuidado.
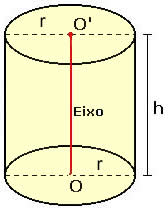
Considere um cilindro circular reto de raio da base r e altura h, como mostra a figura abaixo.
Para compreender como é feito o cálculo de sua área total devemos fazer a planificação do cilindro.
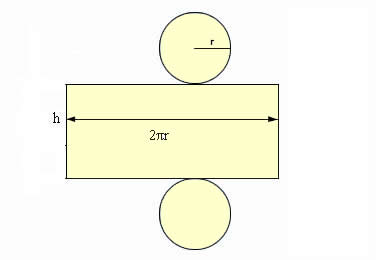Observe que ao planificar o cilindro obtemos duas circunferências de raio r, relativas às duas bases apresentadas no sólido, e um retângulo de altura h e comprimento 2πr. Podemos concluir que:
área total = área lateral + área da base + área da base
Como as bases do cilindro são circunferências de raio r, temos que:
área da base = π∙r2
A área lateral é dada por:
área lateral = 2∙π∙r∙h
Assim, podemos determinar a área total de um cilindro da seguinte forma:
St = 2∙π∙r∙h + 2∙π∙r2
Colocando 2πr em evidência, obtemos:
St = 2∙π∙r∙(h + r)
Que é a fórmula para o cálculo da área total de um cilindro, onde:
St → é a área total
r → é a medida do raio da base
h → é a altura do cilindro
Observe que para calcular a área total do cilindro basta conhecer a medida do raio e da altura.
Vejamos alguns exemplos de aplicação da fórmula da área total.
Exemplo 1. Determine a área total de um cilindro circular reto de 16 cm de altura e raio da base medindo 5 cm. (Use π = 3,14)
Solução: Pelo enunciado do problema temos os seguintes dados:
h = 16 cm
r = 5 cm
St = ?
Utilizando a fórmula da área total, obtemos:
St=2∙π∙r∙(h+r)
St = 2 ∙ 3,14 ∙ 5 ∙(16 + 5)
St = 2 ∙ 3,14 ∙ 5 ∙ 21
St = 659,4 cm2
Exemplo2. Uma indústria deseja fabricar um barril de óleo com formato cilíndrico cujo raio da base deve apresentar 40 cm de comprimento e sua altura será de 1,2 m. Para fabricação desse barril, a indústria utilizará chapas metálicas. Quantos metros quadrados de chapa serão necessários para fabricar um barril? (Use π = 3,14)
Solução: A resolução desse problema consiste em determinar a área total desse barril, que apresenta o formato de um cilindro. Do enunciado do problema, obtemos:
h = 1,2 m
r = 40 cm = 0,4 m
St = ?
Pela fórmula da área total, temos que:
St = 2∙π∙r∙(h + r)
St = 2 ∙ 3,14 ∙ 0,4 ∙ (1,2 + 0,4)
St = 2 ∙ 3,14 ∙ 0,4 ∙ 1,6
St = 4,02 m2
Portanto, serão gastos, aproximadamente, 4,02 metros quadrados de chapa metálica para confeccionar um barril.
Exemplo 3. Uma lata de extrato de tomate de formato cilíndrico possui área total de 244,92 cm2 de área total. Sabendo que o raio da base da lata mede 3 cm, obtenha a medida da altura dessa embalagem.
Solução: Pelo enunciado do problema, obtemos:
St = 244,92 cm2
h = ?
r = 3 cm
Utilizando a fórmula da área total, temos que:
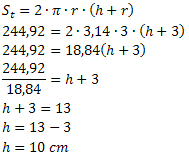
Portanto, a lata possui uma altura de 10 cm.
- Areas E Volume Do Cilindro
Área Lateral : Al A superfície lateral de um cilindro é a reunião das geratrizes. A área dessa superfície é chamada área lateral do cilindro e é indicada por Al. A superfície lateral de um cilindro circular reto, de altura h, e cujos círculos...
- Área Total Do Cone
Por Marcelo Rigonatto ConeO cone é um sólido geométrico classificado como corpo redondo por apresentar, assim como o cilindro, uma de suas faces arredondadas. Ele pode ser considerado um tipo especial de...
- Área Total Do Cone
ConeO cone é um sólido geométrico classificado como corpo redondo por apresentar, assim como o cilindro, uma de suas faces arredondadas. Ele pode ser considerado um tipo especial de pirâmide, sendo que algumas de suas propriedades são semelhantes...
- Cilindro
O cilindro é um corpo redondo com duas bases opostas e paralelas. Podem ser classificados, de acordo com a inclinação da geratriz em relação aos planos das bases, em: cilindro circular oblíquo (a geratriz é oblíqua às bases) e cilindro circular...
- Área Total Do Cone
Área total do coneMarcelo Rigonatto ConeO cone é um sólido geométrico classificado como corpo redondo por apresentar, assim como o cilindro, uma de suas faces arredondadas. Ele pode ser considerado um tipo especial de pirâmide,...
Matemática
Área total do cilindro
Área total do cilindro
Marcelo Rigonatto Cilindros
Considere um cilindro circular reto de raio da base r e altura h, como mostra a figura abaixo.
área total = área lateral + área da base + área da base
Como as bases do cilindro são circunferências de raio r, temos que:
área da base = π∙r2
A área lateral é dada por:
área lateral = 2∙π∙r∙h
Assim, podemos determinar a área total de um cilindro da seguinte forma:
St = 2∙π∙r∙h + 2∙π∙r2
Colocando 2πr em evidência, obtemos:
St = 2∙π∙r∙(h + r)
Que é a fórmula para o cálculo da área total de um cilindro, onde:
St → é a área total
r → é a medida do raio da base
h → é a altura do cilindro
Observe que para calcular a área total do cilindro basta conhecer a medida do raio e da altura.
Vejamos alguns exemplos de aplicação da fórmula da área total.
Exemplo 1. Determine a área total de um cilindro circular reto de 16 cm de altura e raio da base medindo 5 cm. (Use π = 3,14)
Solução: Pelo enunciado do problema temos os seguintes dados:
h = 16 cm
r = 5 cm
St = ?
Utilizando a fórmula da área total, obtemos:
St=2∙π∙r∙(h+r)
St = 2 ∙ 3,14 ∙ 5 ∙(16 + 5)
St = 2 ∙ 3,14 ∙ 5 ∙ 21
St = 659,4 cm2
Exemplo2. Uma indústria deseja fabricar um barril de óleo com formato cilíndrico cujo raio da base deve apresentar 40 cm de comprimento e sua altura será de 1,2 m. Para fabricação desse barril, a indústria utilizará chapas metálicas. Quantos metros quadrados de chapa serão necessários para fabricar um barril? (Use π = 3,14)
Solução: A resolução desse problema consiste em determinar a área total desse barril, que apresenta o formato de um cilindro. Do enunciado do problema, obtemos:
h = 1,2 m
r = 40 cm = 0,4 m
St = ?
Pela fórmula da área total, temos que:
St = 2∙π∙r∙(h + r)
St = 2 ∙ 3,14 ∙ 0,4 ∙ (1,2 + 0,4)
St = 2 ∙ 3,14 ∙ 0,4 ∙ 1,6
St = 4,02 m2
Portanto, serão gastos, aproximadamente, 4,02 metros quadrados de chapa metálica para confeccionar um barril.
Exemplo 3. Uma lata de extrato de tomate de formato cilíndrico possui área total de 244,92 cm2 de área total. Sabendo que o raio da base da lata mede 3 cm, obtenha a medida da altura dessa embalagem.
Solução: Pelo enunciado do problema, obtemos:
St = 244,92 cm2
h = ?
r = 3 cm
Utilizando a fórmula da área total, temos que:
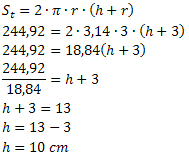
Portanto, a lata possui uma altura de 10 cm.
- Areas E Volume Do Cilindro
Área Lateral : Al A superfície lateral de um cilindro é a reunião das geratrizes. A área dessa superfície é chamada área lateral do cilindro e é indicada por Al. A superfície lateral de um cilindro circular reto, de altura h, e cujos círculos...
- Área Total Do Cone
Por Marcelo Rigonatto ConeO cone é um sólido geométrico classificado como corpo redondo por apresentar, assim como o cilindro, uma de suas faces arredondadas. Ele pode ser considerado um tipo especial de...
- Área Total Do Cone
ConeO cone é um sólido geométrico classificado como corpo redondo por apresentar, assim como o cilindro, uma de suas faces arredondadas. Ele pode ser considerado um tipo especial de pirâmide, sendo que algumas de suas propriedades são semelhantes...
- Cilindro
O cilindro é um corpo redondo com duas bases opostas e paralelas. Podem ser classificados, de acordo com a inclinação da geratriz em relação aos planos das bases, em: cilindro circular oblíquo (a geratriz é oblíqua às bases) e cilindro circular...
- Área Total Do Cone
Área total do coneMarcelo Rigonatto ConeO cone é um sólido geométrico classificado como corpo redondo por apresentar, assim como o cilindro, uma de suas faces arredondadas. Ele pode ser considerado um tipo especial de pirâmide,...