Matemática
Na Análise Combinatória, os agrupamentos de elementos que se diferem entre si pela ordem ou pela natureza dos elementos são chamados de Arranjos. Por exemplo, em uma situação envolvendo os números 2, 4, 6 e 8, se formarmos números de três algarismos distintos, podemos ter a seguinte situação:
246 ≠ 642
Observe que os mesmos elementos formam números diferentes, essa é uma característica marcante no agrupamento por Arranjos. O número total de Arranjos de um grupo de elementos pode ser calculado pela expressão:

Na resolução dessa fórmula devemos lembrar que o símbolo matemático dado por ! (fatorial), significa a multiplicação do número indicado por todos os seus antecessores naturais com ausência do zero. Por exemplo:
4! = 4 * 3 * 2 * 1 = 24
5! = 5 * 4 * 3 * 2 * 1 = 120
7! = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5040
10! = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 3.628.800
Exemplo 1
Quantos números de três algarismos diferentes podemos escrever com os elementos 1, 2, 3, 4, 5, 6, 7, 8 e 9?
Vamos arranjar os números da seguinte forma: 9 elementos agrupados 3 a 3.

Podemos formar 504 números.
Exemplo 2
Em uma sala de espera existem 8 cadeiras. Considerando que em um dia 12 pessoas esperavam para serem atendidas, determine quantas maneiras diferentes essas pessoas podem se sentar.

As pessoas podem se sentar de 11.880 maneiras diferentes.
Exemplo 3
Uma associação é formada por 20 membros. Considerando que a diretoria é formada por um presidente, um vice-presidente, um secretário e um tesoureiro, determine de quantas maneiras é possível formar a diretoria.
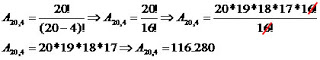
A diretoria da associação poderá ser formada por 116.280 maneiras.
Exemplo 4
Dado os números 1, 2, 3, 4, 5, 6, 7, 8 e 9, determine a quantidade de números pares de 5 algarismos não repetidos que podemos formar.
Dos algarismos fornecidos temos que 4 são pares, dessa forma, os números a serem formados devem terminar com eles. Observe:
____ ____ ____ ____ 2
____ ____ ____ ____ 4
____ ____ ____ ____ 6
____ ____ ____ ____ 8
Assim, escreveremos A8,4 números de 4 algarismos, e como são 4 possibilidades de terminação, o resultado de A8,4, deverá ser multiplicado por 4.

A partir das condições impostas é possível formar 6.720 maneiras.
www.bancodeconcursos.com
- OperaÇÕes Com PolinÔmios
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso Colégio Estadual Dinah Gonçalves www.accbarrosogestar.wordpress.com email [email protected] HTTP://ensinodematemtica.blogspot.com extraído do http://jmpmat2.blogspot.com/...
- Permutação
Considere um conjunto C com n elementos distintos. Permutação simples é o arranjo desses n elementos, tomados n a n. Uma característica das permutações é que elas são agrupamentos formados pelos mesmos elementos, diferindo entre si apenas pela...
- Arranjos
Os agrupamentos formados nos exercícios de análise combinatória podem ser considerados Arranjos simples. Será assim classificado se levarmos em consideração a ordem de seus elementos, ou seja, se os agrupamentos forem diferentes entre si pela ordem...
- Anagrama
O anagrama é um jogo de palavras que utiliza a transposição ou rearranjo de letras de uma palavra ou frase, com o intuito de formar outras palavras com ou sem sentido. É calculado através da propriedade fundamental da contagem, utilizando o fatorial...
- OperaÇÕes Com PolinÔmios
ADIÇÃO DE POLINÔMIOS EXEMPLO Vamos calcular: (3x²- 6x + 4) + (2x² + 4x – 7)= =3x²-6x+4+2x²+4x-7= =3x²+2x²-6x+4x+4-6= =5x²-2x-3 EXERCÍCIOS 1) Efetue as seguintes adições de polinômios: a) (2x²-9x+2)+(3x²+7x-1) _______ (R:5x² -2x...
Matemática
Arranjos Simples
Na Análise Combinatória, os agrupamentos de elementos que se diferem entre si pela ordem ou pela natureza dos elementos são chamados de Arranjos. Por exemplo, em uma situação envolvendo os números 2, 4, 6 e 8, se formarmos números de três algarismos distintos, podemos ter a seguinte situação:
246 ≠ 642
Observe que os mesmos elementos formam números diferentes, essa é uma característica marcante no agrupamento por Arranjos. O número total de Arranjos de um grupo de elementos pode ser calculado pela expressão:

Na resolução dessa fórmula devemos lembrar que o símbolo matemático dado por ! (fatorial), significa a multiplicação do número indicado por todos os seus antecessores naturais com ausência do zero. Por exemplo:
4! = 4 * 3 * 2 * 1 = 24
5! = 5 * 4 * 3 * 2 * 1 = 120
7! = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5040
10! = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 3.628.800
Exemplo 1
Quantos números de três algarismos diferentes podemos escrever com os elementos 1, 2, 3, 4, 5, 6, 7, 8 e 9?
Vamos arranjar os números da seguinte forma: 9 elementos agrupados 3 a 3.

Podemos formar 504 números.
Exemplo 2
Em uma sala de espera existem 8 cadeiras. Considerando que em um dia 12 pessoas esperavam para serem atendidas, determine quantas maneiras diferentes essas pessoas podem se sentar.

As pessoas podem se sentar de 11.880 maneiras diferentes.
Exemplo 3
Uma associação é formada por 20 membros. Considerando que a diretoria é formada por um presidente, um vice-presidente, um secretário e um tesoureiro, determine de quantas maneiras é possível formar a diretoria.
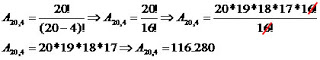
A diretoria da associação poderá ser formada por 116.280 maneiras.
Exemplo 4
Dado os números 1, 2, 3, 4, 5, 6, 7, 8 e 9, determine a quantidade de números pares de 5 algarismos não repetidos que podemos formar.
Dos algarismos fornecidos temos que 4 são pares, dessa forma, os números a serem formados devem terminar com eles. Observe:
____ ____ ____ ____ 2
____ ____ ____ ____ 4
____ ____ ____ ____ 6
____ ____ ____ ____ 8
Assim, escreveremos A8,4 números de 4 algarismos, e como são 4 possibilidades de terminação, o resultado de A8,4, deverá ser multiplicado por 4.

A partir das condições impostas é possível formar 6.720 maneiras.
www.bancodeconcursos.com
- OperaÇÕes Com PolinÔmios
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso Colégio Estadual Dinah Gonçalves www.accbarrosogestar.wordpress.com email [email protected] HTTP://ensinodematemtica.blogspot.com extraído do http://jmpmat2.blogspot.com/...
- Permutação
Considere um conjunto C com n elementos distintos. Permutação simples é o arranjo desses n elementos, tomados n a n. Uma característica das permutações é que elas são agrupamentos formados pelos mesmos elementos, diferindo entre si apenas pela...
- Arranjos
Os agrupamentos formados nos exercícios de análise combinatória podem ser considerados Arranjos simples. Será assim classificado se levarmos em consideração a ordem de seus elementos, ou seja, se os agrupamentos forem diferentes entre si pela ordem...
- Anagrama
O anagrama é um jogo de palavras que utiliza a transposição ou rearranjo de letras de uma palavra ou frase, com o intuito de formar outras palavras com ou sem sentido. É calculado através da propriedade fundamental da contagem, utilizando o fatorial...
- OperaÇÕes Com PolinÔmios
ADIÇÃO DE POLINÔMIOS EXEMPLO Vamos calcular: (3x²- 6x + 4) + (2x² + 4x – 7)= =3x²-6x+4+2x²+4x-7= =3x²+2x²-6x+4x+4-6= =5x²-2x-3 EXERCÍCIOS 1) Efetue as seguintes adições de polinômios: a) (2x²-9x+2)+(3x²+7x-1) _______ (R:5x² -2x...
