Matemática
EQUAÇÕES DO 1º GRAU COM DUAS VARIAVEIS
* Definição
É definido como equação do primeiro grau com duas variáveis sejam elas, x e y, a toda e qualquer equação que pode ser indicada nas formas:
ax + by = c
Sendo que: a e b, são números e diferentes de zero ( a e b ≠ 0 ), respectivamente.
Exemplos:
3x – 4y = 2 » os número “x” e “y” que são desconhecidos recebem os termos de incógnita.
3y + 4x = 7 » os número “y” e “x” que são desconhecidos recebem os termos de incógnita.
* Solução de equação do 1º grau com “duas” variáveis
As equações do primeiro grau que estejam na forma com duas variáveis, x e y, possuem infinitas soluções.
Estas soluções infinitas podem ser obtidas dando valores “soltos” para uma das variáveis, e em seguida efetua-se o cálculo da outra variável.
Encontrando estes valores de x e y, significa dizer que foi obtido o par ordenado de números x e y, o qual tornará a sentença ou o problema fornecido verdadeiro.
Exemplo de fixação:
a) 3x + 2y = 20
Como já informado esta equação tem infinitas soluções:
1) x = 2
3x + 2y = 20
3.2 + 2y = 20
2y = 20 – 6
2y = 14
y = 7
Assim, temos o par ordenado x e y (2 e 7).
Veja se a sentença é verdadeira:
3x + 2y = 20 (quando x = 2, y = 7)
3.2 + 2.7 = 20
6 + 14 = 20
20 = 20
b) 2x + 4y = 8
Agora tomaremos os valores de x e y respectivamente:
x = 2 e y = 6
2x + 4y = 8
2.2 + 4.6 = 8
4 + 24 = 8
28 ≠ 8
Desta forma, o par 2 e 6 não é a solução verdadeira para o a sentença acima.
* Linguagem textual para soluções de problemas
Para que se possam resolver problemas com equações do 1º grau, é preciso traduzir alguns enunciados para linguagem em moldes matemáticos.
Observe abaixo:
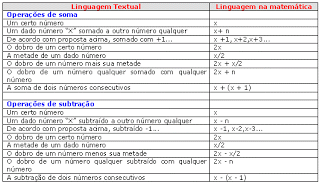
* Exercícios resolvidos de equações de 1º grau com “uma” e “duas” variáveis
01 – Em um sítio, entre ovelhas e cabritos, há 200 animais. Se o número de ovelhas é igual a 1/3 do número de cabritos, determine quantas são o número de ovelhas e quantos são o número de cabritos.
R.: Este problema se trata de uma equação do 1º grau com duas variáveis (ovelhas e cabritos).
Solução:
x = ovelhas
y = cabritos
Sabendo que x é igual 1/3 do total de 200 animais, temos o valor de ovelhas = 67 (valor arred.)
assim: x + y = 200
67 + y = 200
y = 200 – 67
y = 133 >> S = {67,133}
Existem, desta forma, 67 ovelhas e 133 cabritos, totalizando 200 animais.
02 – Em um quintal existem porcos, avestruz e galinhas, fazendo um total de 60 cabeças e 180 pés.
Quantos são os animais de duas patas e quantos são os de quatro patas?
R.: Este problema se trata de uma equação do 1º grau com duas variáveis (animais de duas patas e animais de quatro patas).
Solução:
x = animais de duas patas (avestruz e galinhas)
y = animais de quatro patas (porcos)
x + y = 60 >> x = 60 – y
Assim: animais de duas pernas 2x, e quatro pernas 4y, logo são observados.
2x + 4y = 180
2(60 – y) + 4y = 180
120 – 2y + 4y = 180
2y = 180 – 120
2y = 60 >> y = 30
x + y = 60
x + 30 = 60
x = 60 -30 >> x = 30 >> S = {30,30}
Existem, então, 30 animais de 02 pernas e 30 animais de 04 pernas.
03 – Determine os valores da incógnita “x”, nas expressões abaixo:
a) 2x + 6 = 0
2x = -6
x = -6/2
x = -3 >> V = {-3}
b) 5x + 4 = 5 + 4x
5x – 4x = 5 – 4
x = 1 >> V = {1}
c) -10x + 6 = -18 + 2x
-10x – 2x = -18 – 6
-12x = -24 (.-1) , multiplicar por (-1), pois a variável x está com valor negativo
12x = 24
x = 24/12 >> x = 2 >> V = {2}
04 – A soma de dois números dados é 8 e a diferença entre estes mesmos números é igual a 4. Quais sãos os números?
R.: Este problema se trata de uma equação do 1º grau com duas variáveis (aplica-se aqui o estudo da linguagem textual).
x + y = 8
x – y = 4
x + x + y – y = 8 + 4
2x = 12
x = 12/2 >> x = 6
x – y = 4
6 – y = 4
-y = 4 – 6
-y = -2 (.-1) >> y = 2 >> S = {6,2}
- Sistema De Equação
Equações do 1º grau com uma variável Equação é toda sentença matemática aberta representada por uma igualdade, em que exista uma ou mais letras que representam números desconhecidos. Exemplo:X + 3 = 12 – 4 Forma geral: ax = b, em que...
- Sistema De Equação
Gráfico de uma equação de 1º grau com duas variáveis Sabemos que uma equação do 1º grau com duas variáveis possui infinitas soluções. Cada uma dessas soluções pode ser representada por um par ordenado (x, y). Dispondo de dois pares ordenados...
- Equação De 1º Grau
~EQUAÇÃO DO 1º GRAU * Definição É definido como uma equação como toda e qualquer igualdade (=) que somente pode ser satisfeita para alguns valores que estejam agregados em seus domínios. Exemplos: 3x – 4 = 2 à o número X que é desconhecido...
- Sistema De Equação
Equações do 1º grau com uma variável Equação é toda sentença matemática aberta representada por uma igualdade, em que exista uma ou mais letras que representam números desconhecidos. Exemplo:X + 3 = 12 – 4 Forma geral: ax = b, em que...
- EquaÇÃo De 1° Grau
EQUAÇÃO DE 1° GRAU SENTENÇAS Uma sentença matemática pode ser verdadeira ou falsa exemplo de uma sentença verdadeira a) 15 + 10 = 25 b) 2 . 5 = 10 exemplo de uma sentença falsa a) 10 + 3 = 18 b) 3 . 7 = 20 SENTEÇAS ABERTAS E SENTENÇAS FECHADAS...
Matemática
Equação com duas variaveis
EQUAÇÕES DO 1º GRAU COM DUAS VARIAVEIS
* Definição
É definido como equação do primeiro grau com duas variáveis sejam elas, x e y, a toda e qualquer equação que pode ser indicada nas formas:
ax + by = c
Sendo que: a e b, são números e diferentes de zero ( a e b ≠ 0 ), respectivamente.
Exemplos:
3x – 4y = 2 » os número “x” e “y” que são desconhecidos recebem os termos de incógnita.
3y + 4x = 7 » os número “y” e “x” que são desconhecidos recebem os termos de incógnita.
* Solução de equação do 1º grau com “duas” variáveis
As equações do primeiro grau que estejam na forma com duas variáveis, x e y, possuem infinitas soluções.
Estas soluções infinitas podem ser obtidas dando valores “soltos” para uma das variáveis, e em seguida efetua-se o cálculo da outra variável.
Encontrando estes valores de x e y, significa dizer que foi obtido o par ordenado de números x e y, o qual tornará a sentença ou o problema fornecido verdadeiro.
Exemplo de fixação:
a) 3x + 2y = 20
Como já informado esta equação tem infinitas soluções:
1) x = 2
3x + 2y = 20
3.2 + 2y = 20
2y = 20 – 6
2y = 14
y = 7
Assim, temos o par ordenado x e y (2 e 7).
Veja se a sentença é verdadeira:
3x + 2y = 20 (quando x = 2, y = 7)
3.2 + 2.7 = 20
6 + 14 = 20
20 = 20
b) 2x + 4y = 8
Agora tomaremos os valores de x e y respectivamente:
x = 2 e y = 6
2x + 4y = 8
2.2 + 4.6 = 8
4 + 24 = 8
28 ≠ 8
Desta forma, o par 2 e 6 não é a solução verdadeira para o a sentença acima.
* Linguagem textual para soluções de problemas
Para que se possam resolver problemas com equações do 1º grau, é preciso traduzir alguns enunciados para linguagem em moldes matemáticos.
Observe abaixo:

* Exercícios resolvidos de equações de 1º grau com “uma” e “duas” variáveis
01 – Em um sítio, entre ovelhas e cabritos, há 200 animais. Se o número de ovelhas é igual a 1/3 do número de cabritos, determine quantas são o número de ovelhas e quantos são o número de cabritos.
R.: Este problema se trata de uma equação do 1º grau com duas variáveis (ovelhas e cabritos).
Solução:
x = ovelhas
y = cabritos
Sabendo que x é igual 1/3 do total de 200 animais, temos o valor de ovelhas = 67 (valor arred.)
assim: x + y = 200
67 + y = 200
y = 200 – 67
y = 133 >> S = {67,133}
Existem, desta forma, 67 ovelhas e 133 cabritos, totalizando 200 animais.
02 – Em um quintal existem porcos, avestruz e galinhas, fazendo um total de 60 cabeças e 180 pés.
Quantos são os animais de duas patas e quantos são os de quatro patas?
R.: Este problema se trata de uma equação do 1º grau com duas variáveis (animais de duas patas e animais de quatro patas).
Solução:
x = animais de duas patas (avestruz e galinhas)
y = animais de quatro patas (porcos)
x + y = 60 >> x = 60 – y
Assim: animais de duas pernas 2x, e quatro pernas 4y, logo são observados.
2x + 4y = 180
2(60 – y) + 4y = 180
120 – 2y + 4y = 180
2y = 180 – 120
2y = 60 >> y = 30
x + y = 60
x + 30 = 60
x = 60 -30 >> x = 30 >> S = {30,30}
Existem, então, 30 animais de 02 pernas e 30 animais de 04 pernas.
03 – Determine os valores da incógnita “x”, nas expressões abaixo:
a) 2x + 6 = 0
2x = -6
x = -6/2
x = -3 >> V = {-3}
b) 5x + 4 = 5 + 4x
5x – 4x = 5 – 4
x = 1 >> V = {1}
c) -10x + 6 = -18 + 2x
-10x – 2x = -18 – 6
-12x = -24 (.-1) , multiplicar por (-1), pois a variável x está com valor negativo
12x = 24
x = 24/12 >> x = 2 >> V = {2}
04 – A soma de dois números dados é 8 e a diferença entre estes mesmos números é igual a 4. Quais sãos os números?
R.: Este problema se trata de uma equação do 1º grau com duas variáveis (aplica-se aqui o estudo da linguagem textual).
x + y = 8
x – y = 4
x + x + y – y = 8 + 4
2x = 12
x = 12/2 >> x = 6
x – y = 4
6 – y = 4
-y = 4 – 6
-y = -2 (.-1) >> y = 2 >> S = {6,2}
- Sistema De Equação
Equações do 1º grau com uma variável Equação é toda sentença matemática aberta representada por uma igualdade, em que exista uma ou mais letras que representam números desconhecidos. Exemplo:X + 3 = 12 – 4 Forma geral: ax = b, em que...
- Sistema De Equação
Gráfico de uma equação de 1º grau com duas variáveis Sabemos que uma equação do 1º grau com duas variáveis possui infinitas soluções. Cada uma dessas soluções pode ser representada por um par ordenado (x, y). Dispondo de dois pares ordenados...
- Equação De 1º Grau
~EQUAÇÃO DO 1º GRAU * Definição É definido como uma equação como toda e qualquer igualdade (=) que somente pode ser satisfeita para alguns valores que estejam agregados em seus domínios. Exemplos: 3x – 4 = 2 à o número X que é desconhecido...
- Sistema De Equação
Equações do 1º grau com uma variável Equação é toda sentença matemática aberta representada por uma igualdade, em que exista uma ou mais letras que representam números desconhecidos. Exemplo:X + 3 = 12 – 4 Forma geral: ax = b, em que...
- EquaÇÃo De 1° Grau
EQUAÇÃO DE 1° GRAU SENTENÇAS Uma sentença matemática pode ser verdadeira ou falsa exemplo de uma sentença verdadeira a) 15 + 10 = 25 b) 2 . 5 = 10 exemplo de uma sentença falsa a) 10 + 3 = 18 b) 3 . 7 = 20 SENTEÇAS ABERTAS E SENTENÇAS FECHADAS...
