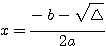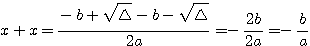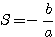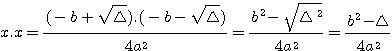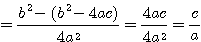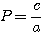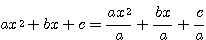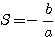Matemática
- Fórmula De Bhaskara
A nome Fórmula de Bhaskara foi dada em homenagem ao matemático Bhaskara Akaria, considerado o mais importante matemático indiano do século XII. A fórmula de Bhaskara é principalmente usada para resolver equações quadráticas de fórmula geral...
- Equação Do 2º Grau
As equações do tipo ax + b = 0, com a e b números reais e a ≠ 0 são consideradas equações do 1º grau, e podem ter no máximo um resultado. Os modelos de expressões que satisfazem a condição ax² + bx + c = 0, com a, b e c números reais e...
- Bháskara : Resolvendo Uma Equação Completa Do 2º Grau
Bháskara : Resolvendo uma Equação Completa do 2º Grau Marcos Noé Fórmula de BháskaraEquações do tipo ax + b = 0, com a e b números reais e a ≠ 0, são consideradas do 1º grau e possuem uma única raiz real. Já as equações...
- Formula De Bhaskara
A nome Fórmula de Bhaskara foi dada em homenagem ao matemático Bhaskara Akaria, considerado o mais importante matemático indiano do século XII. A fórmula de Bhaskara é principalmente usada para resolver equações quadráticas de fórmula geral...
- Formula De Bhaskara
A nome Fórmula de Bhaskara foi dada em homenagem ao matemático Bhaskara Akaria, considerado o mais importante matemático indiano do século XII. A fórmula de Bhaskara é principalmente usada para resolver equações quadráticas de fórmula geral...
Matemática
Equação do 2º Grau
Denomina-se equação do segundo grau, toda a equação do tipo ax²+bx+c, com coeficientes numéricos a.b e c com . Exemplos: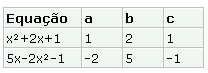 Classificação- Incompletas: Se um dos coeficientes ( b ou c ) for nulo, temos uma equação do 2º grau incompleta.1º caso: b=0 Considere a equação do 2º grau imcompletax²-9=0 » x²=9 » x=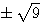 » x= » x=  2º caso: c=0 Considere a equação do 2º grau imcompleta: x²-9x=0 » Basta fatorar o fator comum x x(x-9)=0 » x=0,9 3º caso: b=c=0 2x²=0 » x=0 Resolução de equações do 2º grau: A resolução de equações do 2º grau incompletas já foi explicada acima, vamos agora resolver equações do 2º grau completas, ou seja, do tipo ax²+bx+c=0 com a, b e c diferentes de zero. - Uma equação do 2º grau pode ter até 2 raízes reais, que podem ser determinadas pela fórmula de Bháskara. Como Bháskara chegou até a fórmula de resolução de equações do 2º grau? Considerando a equação: ax²+bx+c=0, vamos determinar a fórmula de Bháskara: Multiplicamos os dois membros por 4a: 4a²x²+4abx+4ac=0 4a²x²+4abx=-4ac Somamos b² aos dois membros: 4a²x²+4abx+b²=b²-4ac Fatoramos o lado esquedo e chamamos de (2ax+b)²= |
- Fórmula De Bhaskara
A nome Fórmula de Bhaskara foi dada em homenagem ao matemático Bhaskara Akaria, considerado o mais importante matemático indiano do século XII. A fórmula de Bhaskara é principalmente usada para resolver equações quadráticas de fórmula geral...
- Equação Do 2º Grau
As equações do tipo ax + b = 0, com a e b números reais e a ≠ 0 são consideradas equações do 1º grau, e podem ter no máximo um resultado. Os modelos de expressões que satisfazem a condição ax² + bx + c = 0, com a, b e c números reais e...
- Bháskara : Resolvendo Uma Equação Completa Do 2º Grau
Bháskara : Resolvendo uma Equação Completa do 2º Grau Marcos Noé Fórmula de BháskaraEquações do tipo ax + b = 0, com a e b números reais e a ≠ 0, são consideradas do 1º grau e possuem uma única raiz real. Já as equações...
- Formula De Bhaskara
A nome Fórmula de Bhaskara foi dada em homenagem ao matemático Bhaskara Akaria, considerado o mais importante matemático indiano do século XII. A fórmula de Bhaskara é principalmente usada para resolver equações quadráticas de fórmula geral...
- Formula De Bhaskara
A nome Fórmula de Bhaskara foi dada em homenagem ao matemático Bhaskara Akaria, considerado o mais importante matemático indiano do século XII. A fórmula de Bhaskara é principalmente usada para resolver equações quadráticas de fórmula geral...

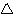 (delta) b²-4ac:
(delta) b²-4ac: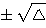
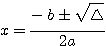 ou
ou 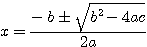
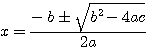
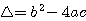 = (-7)²-4.3.2 = 49-24 = 25
= (-7)²-4.3.2 = 49-24 = 25 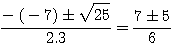
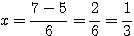
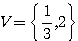
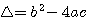 = 4²-4.-1.-4 = 16-16 = 0
= 4²-4.-1.-4 = 16-16 = 0 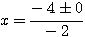 » x=2
» x=2 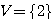
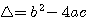 = (-6)²-4.5.5 = 36-100 = -64
= (-6)²-4.5.5 = 36-100 = -64 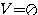 » vazio
» vazio