Matemática
- Função Do 1º Grau
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...
- Gráfico De Uma Função Do 1º Grau
Toda função definida por f(x) = ax + b, com a e b pertencentes aos reais e a 0 é considerada uma função do 1º grau e possui representação gráfica no plano cartesiano. O gráfico de uma função do 1º grau é uma reta podendo ser crescente ou...
- Função De 1º Grau E Inversa
Toda função do 1º grau possui a seguinte lei de formação: y = ax + b, onde a e b são números reais e a ≠ 0. Esse modelo de função contribui na elaboração e resolução de situações problemas cotidianas. Através de exemplos aplicados mostraremos...
- Função Do 1º Grau
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.comGráfico...
- Gráfico Da Função Do 1º Grau
Gráfico da Função do 1º Grau Marcos Noé A reta como gráfico da funçãoNa Matemática, consideramos função como uma relação de dependência entre duas grandezas. As relações que envolvem crescimentos e decrescimentos...
Matemática
Função de 1º grau
Consideremos x e y duas variáveis, sendo uma dependente da outra, isto é, para cada valor atribuído a x corresponde um valor para y. Definimos essa dependência como função, nesse caso, y está em função de x. O conjunto de valores conferidos a x deve ser chamado de domínio da função e os valores de y são a imagem da função.
Toda função é definida por uma lei de formação, no caso de uma função do 1º grau a lei de formação será a seguinte: y = ax + b, onde a e b são números reais e a ≠ 0.
Esse tipo de função deve ser dos Reais para os Reais.
A representação gráfica de uma função do 1º grau é uma reta. Analisando a lei de formação y = ax + b, notamos a dependência entre x e y, e identificamos dois números: a e b. Eles são os coeficientes da função, o valor de a indica se a função é crescente ou decrescente e o valor de b indica o ponto de intersecção da função com o eixo y no plano cartesiano. Observe:
Função crescente Função decrescente
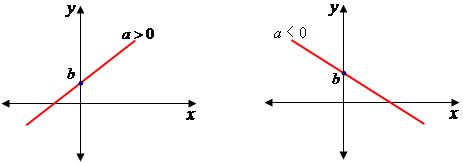
Função crescente: à medida que os valores de x aumentam, os valores correspondentes em y também aumentam.
Função decrescente: à medida que os valores de x aumentam, os valores correspondentes de y diminuem.
Exemplos de funções do 1º grau
y = 4x + 2, a = 4 e b = 2
y = 5x – 9, a = 5 e b = –9
y = – 2x + 10, a = – 2 e b = 10
y = 3x, a = 3 e b = 0
y = – 6x – 1, a = – 6 e b = – 1
Raiz ou zero de uma função do 1º grau
Para determinar a raiz ou o zero de uma função do 1º grau é preciso considerar
y = 0. De acordo com gráfico, no instante em que y assume valor igual a zero, a reta intersecta o eixo x em um determinado ponto, determinando a raiz ou o zero da função.
Vamos determinar a raiz das funções a seguir:
y = 4x + 2y = 0
4x + 2 = 0
4x = –2
x = –2/4
x = –1/2
A reta representada pela função y = 4x + 2 intersecta o eixo x no seguinte valor: –1/2
y = – 2x + 10
y = 0
– 2x + 10 = 0
– 2x = – 10 (–1)
2x = 10
x = 10/2
x = 5
A reta representada pela função y = – 2x + 10 intersecta o eixo x no seguinte valor: 5
Toda função é definida por uma lei de formação, no caso de uma função do 1º grau a lei de formação será a seguinte: y = ax + b, onde a e b são números reais e a ≠ 0.
Esse tipo de função deve ser dos Reais para os Reais.
A representação gráfica de uma função do 1º grau é uma reta. Analisando a lei de formação y = ax + b, notamos a dependência entre x e y, e identificamos dois números: a e b. Eles são os coeficientes da função, o valor de a indica se a função é crescente ou decrescente e o valor de b indica o ponto de intersecção da função com o eixo y no plano cartesiano. Observe:
Função crescente Função decrescente

Função crescente: à medida que os valores de x aumentam, os valores correspondentes em y também aumentam.
Função decrescente: à medida que os valores de x aumentam, os valores correspondentes de y diminuem.
Exemplos de funções do 1º grau
y = 4x + 2, a = 4 e b = 2
y = 5x – 9, a = 5 e b = –9
y = – 2x + 10, a = – 2 e b = 10
y = 3x, a = 3 e b = 0
y = – 6x – 1, a = – 6 e b = – 1
Raiz ou zero de uma função do 1º grau
Para determinar a raiz ou o zero de uma função do 1º grau é preciso considerar
y = 0. De acordo com gráfico, no instante em que y assume valor igual a zero, a reta intersecta o eixo x em um determinado ponto, determinando a raiz ou o zero da função.
Vamos determinar a raiz das funções a seguir:
y = 4x + 2y = 0
4x + 2 = 0
4x = –2
x = –2/4
x = –1/2
A reta representada pela função y = 4x + 2 intersecta o eixo x no seguinte valor: –1/2
y = – 2x + 10
y = 0
– 2x + 10 = 0
– 2x = – 10 (–1)
2x = 10
x = 10/2
x = 5
A reta representada pela função y = – 2x + 10 intersecta o eixo x no seguinte valor: 5
mundo educacao.com.br
- Função Do 1º Grau
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...
- Gráfico De Uma Função Do 1º Grau
Toda função definida por f(x) = ax + b, com a e b pertencentes aos reais e a 0 é considerada uma função do 1º grau e possui representação gráfica no plano cartesiano. O gráfico de uma função do 1º grau é uma reta podendo ser crescente ou...
- Função De 1º Grau E Inversa
Toda função do 1º grau possui a seguinte lei de formação: y = ax + b, onde a e b são números reais e a ≠ 0. Esse modelo de função contribui na elaboração e resolução de situações problemas cotidianas. Através de exemplos aplicados mostraremos...
- Função Do 1º Grau
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.comGráfico...
- Gráfico Da Função Do 1º Grau
Gráfico da Função do 1º Grau Marcos Noé A reta como gráfico da funçãoNa Matemática, consideramos função como uma relação de dependência entre duas grandezas. As relações que envolvem crescimentos e decrescimentos...
