Matemática
O estudo das potências foi introduzido pelos babilônios, os quais utilizavam tábuas no cálculo de juros compostos. Arquimedes e Diofante, por volta do séc. III, divulgaram em suas teorias a utilização de potências; e na Europa, em meados do séc. XIV, Nicole Oresme, numa obra denominada Algorismus proportionum, demonstrava novas notações para potências fracionárias e os primeiros estudos sobre potências irracionais. O matemático francês Nicolas Churquet, introduziu nos moldes matemáticos situações envolvendo expoente zero, expoentes negativos e potências inteiras positivas.
O modelo atual de potenciação foi criado e introduzido por René Descartes, no séc. XVII. Os estudos das propriedades da potenciação, as funções exponenciais e os gráficos construídos no plano cartesiano, constituem uma importante ferramenta da Matemática moderna, auxiliando em diversas áreas como Biologia, Química, Física, Economia, Finanças, Administração, Saúde, Esporte entre outras.
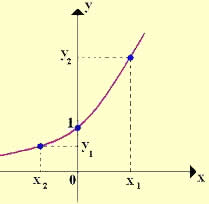
As funções exponenciais são aquelas expressões em que a variável se encontra no expoente, com algumas restrições à base da potência. Esse tipo de função possui a seguinte lei de formação, f(x) = ax ou y = ax, onde a pertence aos reais com ausência do zero, e a diferente de 1.
A função exponencial pode ser classificada em crescente ou decrescente, considerando os seguintes casos:
1º) a > 1 – Crescente
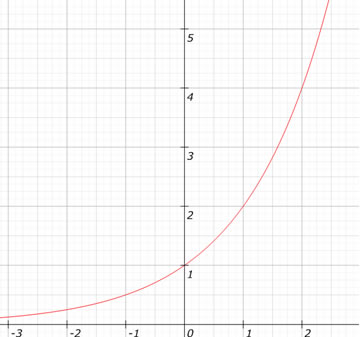
Observe o gráfico da função f(x) = 2x.
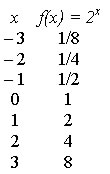
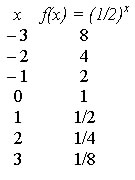
- Gráfico De Uma Função Do 1º Grau
Toda função definida por f(x) = ax + b, com a e b pertencentes aos reais e a 0 é considerada uma função do 1º grau e possui representação gráfica no plano cartesiano. O gráfico de uma função do 1º grau é uma reta podendo ser crescente ou...
- Função Exponencial
As funções exponenciais são utilizadas nas situações envolvendo crescimento e decrescimento, onde a variável está localizada no expoente de uma base. Sua lei de formação é dada pela relação de dependência entre y e x, da seguinte forma: y...
- Função Exponencial
INTRODUÇÃO Seguindo a ordem natural dos artigos sobre Potenciação e Radiciação será abordado agora as equações exponenciais. Antes, será fornecida uma breve noção sobre o conceito e propriedades da função exponencial. Considera-se, também,...
- Função Exponencial
A principal característica de uma função exponencial é o aparecimento da variável no expoente. Esse tipo de função expressa situações onde ocorre grandes variações em períodos curtos. As exponenciais, como são conhecidas, possuem diversas...
- Função Exponencial
Dizemos que uma função é exponencial quando a variável se encontra no expoente de um número real, sendo que esse número precisa ser maior que zero e diferente de um. Podemos explicitar tal condição usando a seguinte definição geral: f: R→R...
Matemática
Gráfico da Função Exponencial
Gráfico da Função Exponencial
Marcos Noé
Curva exponencial
O modelo atual de potenciação foi criado e introduzido por René Descartes, no séc. XVII. Os estudos das propriedades da potenciação, as funções exponenciais e os gráficos construídos no plano cartesiano, constituem uma importante ferramenta da Matemática moderna, auxiliando em diversas áreas como Biologia, Química, Física, Economia, Finanças, Administração, Saúde, Esporte entre outras.
As funções exponenciais são aquelas expressões em que a variável se encontra no expoente, com algumas restrições à base da potência. Esse tipo de função possui a seguinte lei de formação, f(x) = ax ou y = ax, onde a pertence aos reais com ausência do zero, e a diferente de 1.
A função exponencial pode ser classificada em crescente ou decrescente, considerando os seguintes casos:
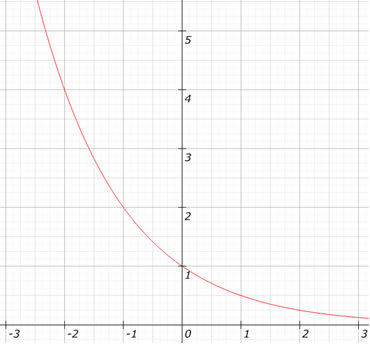
1º) a > 1 – Crescente
Observe o gráfico da função f(x) = 2x.
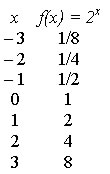

2º) 0 < a < 1 – Decrescente
Observe o gráfico da função f(x) = (1/2)x
Observe o gráfico da função f(x) = (1/2)x
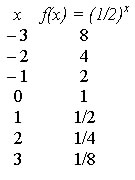

- Gráfico De Uma Função Do 1º Grau
Toda função definida por f(x) = ax + b, com a e b pertencentes aos reais e a 0 é considerada uma função do 1º grau e possui representação gráfica no plano cartesiano. O gráfico de uma função do 1º grau é uma reta podendo ser crescente ou...
- Função Exponencial
As funções exponenciais são utilizadas nas situações envolvendo crescimento e decrescimento, onde a variável está localizada no expoente de uma base. Sua lei de formação é dada pela relação de dependência entre y e x, da seguinte forma: y...
- Função Exponencial
INTRODUÇÃO Seguindo a ordem natural dos artigos sobre Potenciação e Radiciação será abordado agora as equações exponenciais. Antes, será fornecida uma breve noção sobre o conceito e propriedades da função exponencial. Considera-se, também,...
- Função Exponencial
A principal característica de uma função exponencial é o aparecimento da variável no expoente. Esse tipo de função expressa situações onde ocorre grandes variações em períodos curtos. As exponenciais, como são conhecidas, possuem diversas...
- Função Exponencial
Dizemos que uma função é exponencial quando a variável se encontra no expoente de um número real, sendo que esse número precisa ser maior que zero e diferente de um. Podemos explicitar tal condição usando a seguinte definição geral: f: R→R...
