Matemática
A subtração é uma operação básica da Matemática, sendo representada pelo sinal de –. O desenvolvimento da subtração entre números Naturais é de certa forma bem simples. Observe os exemplos:
10 – 2 = 8
12 – 6 = 6
22 – 10 = 12
52 – 12 = 40
101 – 10 = 91
200 – 189 = 11
As operações de subtração envolvendo os números Inteiros requerem algumas situações teóricas que relacionam os possíveis sinais operatórios. Para realizar a subtração entre os números inteiros precisamos ter conhecimento sobre o módulo de um número. Módulo de um número inteiro é calculado obtendo o seu valor real. Observe:
Módulo de +1: representado por |+1| = 1
| – 3| = 3
| – 7| = 7
Regras operatórias:
Sinais iguais: soma e conserva o sinal.
Sinais diferentes: subtrai e conserva o sinal do maior módulo.
Operações sem parênteses
+ 10 – 7 = + 3 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
– 3 – 3 = – 6 (Sinais iguais: soma e conserva o sinal)
+ 20 – 30 = – 10 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
– 12 + 3 = – 9 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
– 9 + 9 = 0 (operação entre números opostos, resultado sempre será 0)
– 25 + 24 = – 1 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
Operações com parênteses
Nesse caso, as operações de subtração podem ser resolvidas eliminando os parênteses, isso será feito aplicando algumas regras que envolvem jogo de sinal, observe:
+ (+) = +
+ (–) = –
– (+) = –
– (–) = +
Eliminado os parênteses, passa a valer as regras operatórias:
(+10) – (–23) = +10 + 23 = + 33
(+20) – (+12) = +20 – 12 = + 8
(–32) + (–5) = – 32 – 5 = – 37
(–27) – (–30) = –27 + 30 = + 3
Em um jogo de somar, as fichas são amarelas ou vermelhas.
Ao tirarmos uma ficha temos que adicionar o número tirado, se a ficha for amarela o número é positivo e se a ficha for vermelha o número é negativo.

Ganha aquele jogador que conseguir ter maior quantidade de pontos.
Eduardo e Mônica começaram a jogar. Eduardo na primeira rodada ficou com +16 pontos, retirou nas rodadas seguintes as fichas . Qual é a situação de Eduardo.
. Qual é a situação de Eduardo.
Vamos fazer os cálculos:
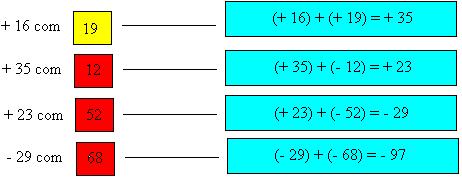
Portanto, Eduardo ao final do jogo estava com – 97 pontos.
Com os cálculos acima podemos concluir que:
Na soma de dois números inteiros com sinais iguais, o valor absoluto será a soma das parcelas, e o sinal será o mesmo das parcelas.
Exemplo: (+ 5) + (+ 4) = + 9
(- 5) + (- 4) = - 9
Na soma de dois números inteiros com sinais diferentes, o valor absoluto será a diferença das parcelas e o sinal será o da parcela de maior valor absoluto.
Exemplo: (- 5) + (+ 4) = - 1
A Soma de dois números inteiros opostos é ZERO.
Exemplo: (+ 10) + (- 10) = 0
Simplificando a escrita:

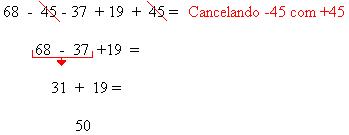
Propriedades da Adição:
►Propriedade do fechamento
(+15) + (+8) = +23
(-34) + (+20) = -14
(-60) + (+60) = 0
A soma de dois números inteiros é sempre um número inteiro.
► Propriedade Comutativa
(+20) + (-43) = -23
(-43) + (+20) = -23
(+20) + (-43) = (-43) + (+20)
A ordem das parcelas não altera a soma
► Propriedade Associativa
[(+10) + (-6)] + (-80) (+10) + [(-6) + (-80)] =
= (+4) + (-80) = -76 (+10) + (-86) = -76
Numa adição de três ou mais parcelas, podemos associar as parcelas de formas diferentes, que os resultados serão iguais.
►Elemento Neutro
(-32) + 0 = 0 + (-32) = -32
(+250) + 0 = 0 + (+250) = +250
O zero é o elemento neutro da adição.
O conjunto dos números inteiros é formado pelos números inteiros positivos e seus respectivos negativos, denominado oposto ou simétrico. A multiplicação entre esses números deverá respeitar algumas regras envolvendo jogo de sinais.
Produto de dois números inteiros com sinais diferentes.
Quando realizamos a multiplicação:
5 x 6 é o mesmo que 6 + 6 + 6 + 6+ 6. Então, para multiplicarmos dois números inteiros com sinais diferentes, iremos utilizar a mesma ideia.
(+5) * (– 2)
(– 2) + (– 2) + (– 2) + (– 2) + (– 2) (Escrevendo uma adição de parcelas iguais)
– 2 – 2 – 2 – 2 – 2 = – 10 (Simplificando a escrita e calculando o resultado)
(+5) * (– 2) = –10
O produto de dois números inteiros, diferente de zero, e de sinais diferentes é um número inteiro de:
Valor absoluto igual ao produto dos valores absolutos dos fatores e sinal negativo (–).
Produto de dois números inteiros com sinais iguais.
Nesse caso há duas possibilidades: dos fatores serem positivos ou dos fatores serem negativos.
Vamos calcular o produto de (+ 8) * (+5) = + 40
Vamos calcular o produto de (– 6) * (– 15) = + 90
O produto de dois números inteiros diferentes de zero e de sinais iguais é um número inteiro de:
Valor absoluto igual ao produto dos valores absolutos dos fatores e sinal positivo (+).
Elemento Neutro
O elemento neutro da multiplicação é 1 ou + 1.
Pois qualquer número inteiro multiplicado por 1 (positivo) será ele mesmo.
Exemplo:
(– 4) * 1 = – 4
(+ 5) * (+ 1) = 5
(–10) * (+1) = – 10
(+ 9) * ( 1 ) = + 9
A multiplicação dos números inteiros é mais simples que a adição e subtração, pois basta multiplicarmos os valores absolutos e o sinal fica conforme a regra:
( + ) * ( + ) = ( + )
( + ) * ( – ) = ( – )
( – ) * ( + ) = ( – )
( – ) * ( – ) = ( + )
Segundo o dicionário Aurélio, divisão significa “partir ou distinguir em diversas partes; separar as diversas partes de.”
Na divisão utilizamos praticamente o mesmo método da multiplicação. Devemos, em primeiro lugar, relembramos o jogo de sinais:
- Divisão de números com mesmo sinal = +
- Divisão de números com sinais diferentes = -
Numa divisão exata de dois números inteiros, o quociente é um número inteiro e o resto é igual a zero.
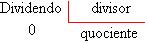
►Quociente de dois números inteiros com sinais diferentes.
(- 45) : (+ 5) = - 9
(+45) : ( -5) = -9
O quociente de uma divisão exata entre dois números inteiros, com divisor diferente de zero e sinais diferentes é um número inteiro de:
Valor absoluto: igual ao quociente dos valores absolutos dos termos.
Sinal: negativo (-).
►Quociente de dois números inteiros com sinais iguais.
(- 60) : (- 10) = + 6
(+ 60) : (+ 10) = + 6
O quociente de uma divisão exata entre dois números inteiros, com divisor diferente de zero e sinais iguais é um número inteiro de:
Valor absoluto: igual ao quociente dos valores absolutos dos termos.
Sinal: positivo (+).
Acontece da mesma forma que na multiplicação, dividimos os valores absolutos e o sinal é conforme a regra:
- : + = -
+ : + = +
- : - = +
Observações:
• Não existe divisão por zero. Exemplo: 15 : 0, pois não existe um número inteiro cujo produto por zero seja 15.
• Zero dividido por qualquer número é sempre zero.
http://www.mundoeducacao.com.br
- Adição De Números Inteiros
Na soma de dois números inteiros com sinais iguais, o valor absoluto será a soma das parcelas, e o sinal será o mesmo das parcelas. Exemplo: (+ 5) + (+ 4) = + 9 (- 5) + (- 4) = - 9 Na soma de dois números inteiros com sinais diferentes, o valor...
- Adição De Números Inteiros
Na soma de dois números inteiros com sinais iguais, o valor absoluto será a soma das parcelas, e o sinal será o mesmo das parcelas. Exemplo: (+ 5) + (+ 4) = + 9 (- 5) + (- 4) = - 9 Na soma de dois números inteiros com sinais diferentes, o valor...
- Adição De Números Inteiros
Na soma de dois números inteiros com sinais iguais, o valor absoluto será a soma das parcelas, e o sinal será o mesmo das parcelas. Exemplo: (+ 5) + (+ 4) = + 9 (- 5) + (- 4) = - 9 Na soma de dois números inteiros com sinais diferentes, o valor...
- Multiplicação De Inteiros
O conjunto dos números inteiros é formado pelos números inteiros positivos e seus respectivos negativos, denominado oposto ou simétrico. A multiplicação entre esses números deverá respeitar algumas regras envolvendo jogo de sinais. Produto de...
- Operações Com Números Inteiros
O conjunto dos números inteiros é formado pelos números inteiros positivos e seus respectivos negativos, denominado oposto ou simétrico. A multiplicação entre esses números deverá respeitar algumas regras envolvendo jogo de sinais. Produto de...
Matemática
Operações com números inteiros
Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email [email protected]
www.ensinodematemtica.blogspot.com.br
www.accbarrosogestar.blogspot.com.br
WWW.profantoniocarneiro.com
A subtração é uma operação básica da Matemática, sendo representada pelo sinal de –. O desenvolvimento da subtração entre números Naturais é de certa forma bem simples. Observe os exemplos:
10 – 2 = 8
12 – 6 = 6
22 – 10 = 12
52 – 12 = 40
101 – 10 = 91
200 – 189 = 11
As operações de subtração envolvendo os números Inteiros requerem algumas situações teóricas que relacionam os possíveis sinais operatórios. Para realizar a subtração entre os números inteiros precisamos ter conhecimento sobre o módulo de um número. Módulo de um número inteiro é calculado obtendo o seu valor real. Observe:
Módulo de +1: representado por |+1| = 1
| – 3| = 3
| – 7| = 7
Regras operatórias:
Sinais iguais: soma e conserva o sinal.
Sinais diferentes: subtrai e conserva o sinal do maior módulo.
Operações sem parênteses
+ 10 – 7 = + 3 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
– 3 – 3 = – 6 (Sinais iguais: soma e conserva o sinal)
+ 20 – 30 = – 10 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
– 12 + 3 = – 9 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
– 9 + 9 = 0 (operação entre números opostos, resultado sempre será 0)
– 25 + 24 = – 1 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
Operações com parênteses
Nesse caso, as operações de subtração podem ser resolvidas eliminando os parênteses, isso será feito aplicando algumas regras que envolvem jogo de sinal, observe:
+ (+) = +
+ (–) = –
– (+) = –
– (–) = +
Eliminado os parênteses, passa a valer as regras operatórias:
(+10) – (–23) = +10 + 23 = + 33
(+20) – (+12) = +20 – 12 = + 8
(–32) + (–5) = – 32 – 5 = – 37
(–27) – (–30) = –27 + 30 = + 3
Em um jogo de somar, as fichas são amarelas ou vermelhas.
Ao tirarmos uma ficha temos que adicionar o número tirado, se a ficha for amarela o número é positivo e se a ficha for vermelha o número é negativo.
Ganha aquele jogador que conseguir ter maior quantidade de pontos.
Eduardo e Mônica começaram a jogar. Eduardo na primeira rodada ficou com +16 pontos, retirou nas rodadas seguintes as fichas
Vamos fazer os cálculos:
Portanto, Eduardo ao final do jogo estava com – 97 pontos.
Com os cálculos acima podemos concluir que:
Na soma de dois números inteiros com sinais iguais, o valor absoluto será a soma das parcelas, e o sinal será o mesmo das parcelas.
Exemplo: (+ 5) + (+ 4) = + 9
(- 5) + (- 4) = - 9
Na soma de dois números inteiros com sinais diferentes, o valor absoluto será a diferença das parcelas e o sinal será o da parcela de maior valor absoluto.
Exemplo: (- 5) + (+ 4) = - 1
A Soma de dois números inteiros opostos é ZERO.
Exemplo: (+ 10) + (- 10) = 0
Simplificando a escrita:
Propriedades da Adição:
►Propriedade do fechamento
(+15) + (+8) = +23
(-34) + (+20) = -14
(-60) + (+60) = 0
A soma de dois números inteiros é sempre um número inteiro.
► Propriedade Comutativa
(+20) + (-43) = -23
(-43) + (+20) = -23
(+20) + (-43) = (-43) + (+20)
A ordem das parcelas não altera a soma
► Propriedade Associativa
[(+10) + (-6)] + (-80) (+10) + [(-6) + (-80)] =
= (+4) + (-80) = -76 (+10) + (-86) = -76
Numa adição de três ou mais parcelas, podemos associar as parcelas de formas diferentes, que os resultados serão iguais.
►Elemento Neutro
(-32) + 0 = 0 + (-32) = -32
(+250) + 0 = 0 + (+250) = +250
O zero é o elemento neutro da adição.
O conjunto dos números inteiros é formado pelos números inteiros positivos e seus respectivos negativos, denominado oposto ou simétrico. A multiplicação entre esses números deverá respeitar algumas regras envolvendo jogo de sinais.
Produto de dois números inteiros com sinais diferentes.
Quando realizamos a multiplicação:
5 x 6 é o mesmo que 6 + 6 + 6 + 6+ 6. Então, para multiplicarmos dois números inteiros com sinais diferentes, iremos utilizar a mesma ideia.
(+5) * (– 2)
(– 2) + (– 2) + (– 2) + (– 2) + (– 2) (Escrevendo uma adição de parcelas iguais)
– 2 – 2 – 2 – 2 – 2 = – 10 (Simplificando a escrita e calculando o resultado)
(+5) * (– 2) = –10
O produto de dois números inteiros, diferente de zero, e de sinais diferentes é um número inteiro de:
Valor absoluto igual ao produto dos valores absolutos dos fatores e sinal negativo (–).
Produto de dois números inteiros com sinais iguais.
Nesse caso há duas possibilidades: dos fatores serem positivos ou dos fatores serem negativos.
Vamos calcular o produto de (+ 8) * (+5) = + 40
Vamos calcular o produto de (– 6) * (– 15) = + 90
O produto de dois números inteiros diferentes de zero e de sinais iguais é um número inteiro de:
Valor absoluto igual ao produto dos valores absolutos dos fatores e sinal positivo (+).
Elemento Neutro
O elemento neutro da multiplicação é 1 ou + 1.
Pois qualquer número inteiro multiplicado por 1 (positivo) será ele mesmo.
Exemplo:
(– 4) * 1 = – 4
(+ 5) * (+ 1) = 5
(–10) * (+1) = – 10
(+ 9) * ( 1 ) = + 9
A multiplicação dos números inteiros é mais simples que a adição e subtração, pois basta multiplicarmos os valores absolutos e o sinal fica conforme a regra:
( + ) * ( + ) = ( + )
( + ) * ( – ) = ( – )
( – ) * ( + ) = ( – )
( – ) * ( – ) = ( + )
Segundo o dicionário Aurélio, divisão significa “partir ou distinguir em diversas partes; separar as diversas partes de.”
Na divisão utilizamos praticamente o mesmo método da multiplicação. Devemos, em primeiro lugar, relembramos o jogo de sinais:
- Divisão de números com mesmo sinal = +
- Divisão de números com sinais diferentes = -
Numa divisão exata de dois números inteiros, o quociente é um número inteiro e o resto é igual a zero.
►Quociente de dois números inteiros com sinais diferentes.
(- 45) : (+ 5) = - 9
(+45) : ( -5) = -9
O quociente de uma divisão exata entre dois números inteiros, com divisor diferente de zero e sinais diferentes é um número inteiro de:
Valor absoluto: igual ao quociente dos valores absolutos dos termos.
Sinal: negativo (-).
►Quociente de dois números inteiros com sinais iguais.
(- 60) : (- 10) = + 6
(+ 60) : (+ 10) = + 6
O quociente de uma divisão exata entre dois números inteiros, com divisor diferente de zero e sinais iguais é um número inteiro de:
Valor absoluto: igual ao quociente dos valores absolutos dos termos.
Sinal: positivo (+).
Acontece da mesma forma que na multiplicação, dividimos os valores absolutos e o sinal é conforme a regra:
- : + = -
+ : + = +
- : - = +
Observações:
• Não existe divisão por zero. Exemplo: 15 : 0, pois não existe um número inteiro cujo produto por zero seja 15.
• Zero dividido por qualquer número é sempre zero.
http://www.mundoeducacao.com.br
- Adição De Números Inteiros
Na soma de dois números inteiros com sinais iguais, o valor absoluto será a soma das parcelas, e o sinal será o mesmo das parcelas. Exemplo: (+ 5) + (+ 4) = + 9 (- 5) + (- 4) = - 9 Na soma de dois números inteiros com sinais diferentes, o valor...
- Adição De Números Inteiros
Na soma de dois números inteiros com sinais iguais, o valor absoluto será a soma das parcelas, e o sinal será o mesmo das parcelas. Exemplo: (+ 5) + (+ 4) = + 9 (- 5) + (- 4) = - 9 Na soma de dois números inteiros com sinais diferentes, o valor...
- Adição De Números Inteiros
Na soma de dois números inteiros com sinais iguais, o valor absoluto será a soma das parcelas, e o sinal será o mesmo das parcelas. Exemplo: (+ 5) + (+ 4) = + 9 (- 5) + (- 4) = - 9 Na soma de dois números inteiros com sinais diferentes, o valor...
- Multiplicação De Inteiros
O conjunto dos números inteiros é formado pelos números inteiros positivos e seus respectivos negativos, denominado oposto ou simétrico. A multiplicação entre esses números deverá respeitar algumas regras envolvendo jogo de sinais. Produto de...
- Operações Com Números Inteiros
O conjunto dos números inteiros é formado pelos números inteiros positivos e seus respectivos negativos, denominado oposto ou simétrico. A multiplicação entre esses números deverá respeitar algumas regras envolvendo jogo de sinais. Produto de...
