Matemática
Portanto, com a palavra ITALIANA podemos formar 3360 anagramas.
Exemplo 3:
Quantos anagramas com a palavra BARREIRA podem ser formados, sendo que deverá começar com a letra B?
B ___ ___ ___ ___ ___ ___ ___
↓ ↓
1 P2,37
1 . P2,37 = 7! = 420
2! . 3!
Portanto, com a palavra BARREIRA podemos formar 420 anagramas.
- Permutações
Entendemos por permutações uma sequência ordenada, construída por elementos disponíveis. O número de permutações de n elementos é dado pelo fatorial de n, isto é, basta calcularmos o fatorial do número de elementos do conjunto fornecido. Para...
- Analíse Combinatorio
Análise Combinatória é um conjunto de procedimentos que possibilita a construção de grupos diferentes formados por um número finito de elementos de um conjunto sob certas circunstâncias. Na maior parte das vezes, tomaremos conjuntos Z com m elementos...
- Probabilidades
O anagrama é um jogo de palavras que utiliza a transposição ou rearranjo de letras de uma palavra ou frase, com o intuito de formar outras palavras com ou sem sentido. É calculado através da propriedade fundamental da contagem, utilizando o fatorial...
- Anagrama
A restrição principal para as permutações simples é quanto aos elementos que serão permutados, pois é necessário que estes sejam distintos, ou seja, que não se repitam. Entretanto, nem sempre conseguiremos situações nas quais os elementos serão...
- Anagrama
O anagrama é um jogo de palavras que utiliza a transposição ou rearranjo de letras de uma palavra ou frase, com o intuito de formar outras palavras com ou sem sentido. É calculado através da propriedade fundamental da contagem, utilizando o fatorial...
Matemática
Permutação com elementos repetidos
Permutação de elementos repetidos deve seguir uma forma diferente da permutação, pois elementos repetidos permutam entre si. Para compreender como isso acontece veja o exemplo abaixo:
A permutação da palavra MATEMÁTICA ficaria da seguinte forma:
Sem levar em consideração as letras (elementos) repetidas, a permutação ficaria assim:
P10 = 10! = 3.628.800
Agora, como a palavra MATEMÁTICA possui elementos que repetem, como a letra A que repete 3 vezes, a letra T repete 2 vezes e a letra M repete 2 vezes, assim a permutação entre si dessas repetições seria 3! . 2! . 2!. Portanto, a permutação da palavra MATEMÁTICA será:

Portanto, com a palavra MATEMÁTICA podemos montar 151200 anagramas.
Seguindo esse raciocínio podemos concluir que, de uma maneira geral, a permutação com elementos repetidos é calculada utilizando a seguinte fórmula:
Dada a permutação de um conjunto com n elementos, alguns elementos repetem n1 vezes, n2 vezes e nnvezes. Então, a permutação é calculada:

Exemplo 1:
Quantos anagramas podem ser formados com a palavra MARAJOARA, aplicando a permutação teremos:
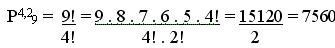
Portanto, com a palavra MARAJOARA podemos formar 7560 anagramas.
Exemplo 2:
Quantos anagramas podem ser formados com a palavra ITALIANA, aplicando a permutação teremos:

A permutação da palavra MATEMÁTICA ficaria da seguinte forma:
Sem levar em consideração as letras (elementos) repetidas, a permutação ficaria assim:
P10 = 10! = 3.628.800
Agora, como a palavra MATEMÁTICA possui elementos que repetem, como a letra A que repete 3 vezes, a letra T repete 2 vezes e a letra M repete 2 vezes, assim a permutação entre si dessas repetições seria 3! . 2! . 2!. Portanto, a permutação da palavra MATEMÁTICA será:

Portanto, com a palavra MATEMÁTICA podemos montar 151200 anagramas.
Seguindo esse raciocínio podemos concluir que, de uma maneira geral, a permutação com elementos repetidos é calculada utilizando a seguinte fórmula:
Dada a permutação de um conjunto com n elementos, alguns elementos repetem n1 vezes, n2 vezes e nnvezes. Então, a permutação é calculada:
Exemplo 1:
Quantos anagramas podem ser formados com a palavra MARAJOARA, aplicando a permutação teremos:
Portanto, com a palavra MARAJOARA podemos formar 7560 anagramas.
Exemplo 2:
Quantos anagramas podem ser formados com a palavra ITALIANA, aplicando a permutação teremos:
Portanto, com a palavra ITALIANA podemos formar 3360 anagramas.
Exemplo 3:
Quantos anagramas com a palavra BARREIRA podem ser formados, sendo que deverá começar com a letra B?
B ___ ___ ___ ___ ___ ___ ___
↓ ↓
1 P2,37
1 . P2,37 = 7! = 420
2! . 3!
Portanto, com a palavra BARREIRA podemos formar 420 anagramas.
Por Danielle de MIranda
Graduada em Matemática
Graduada em Matemática
- Permutações
Entendemos por permutações uma sequência ordenada, construída por elementos disponíveis. O número de permutações de n elementos é dado pelo fatorial de n, isto é, basta calcularmos o fatorial do número de elementos do conjunto fornecido. Para...
- Analíse Combinatorio
Análise Combinatória é um conjunto de procedimentos que possibilita a construção de grupos diferentes formados por um número finito de elementos de um conjunto sob certas circunstâncias. Na maior parte das vezes, tomaremos conjuntos Z com m elementos...
- Probabilidades
O anagrama é um jogo de palavras que utiliza a transposição ou rearranjo de letras de uma palavra ou frase, com o intuito de formar outras palavras com ou sem sentido. É calculado através da propriedade fundamental da contagem, utilizando o fatorial...
- Anagrama
A restrição principal para as permutações simples é quanto aos elementos que serão permutados, pois é necessário que estes sejam distintos, ou seja, que não se repitam. Entretanto, nem sempre conseguiremos situações nas quais os elementos serão...
- Anagrama
O anagrama é um jogo de palavras que utiliza a transposição ou rearranjo de letras de uma palavra ou frase, com o intuito de formar outras palavras com ou sem sentido. É calculado através da propriedade fundamental da contagem, utilizando o fatorial...
