Matemática
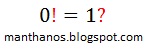



!})
!}=\frac{n!}{n!0!}=\frac{1}{0!})




- Combinações
Combinação simples é um tipo de agrupamento no estudo sobre análise combinatória. Os agrupamentos formados com os elementos de um conjunto serão considerados combinações simples se os elementos dos agrupamentos diferenciarem apenas pela sua natureza....
- Combinações
Seja C um conjunto com m elementos distintos. No estudo de arranjos, já vimos antes que é possível escolher p elementos de A, mas quando realizamos tais escolhas pode acontecer que duas coleções com p elementos tenham os mesmos elementos em ordens...
- Combinações
Combinação simples é um tipo de agrupamento no estudo sobre análise combinatória. Os agrupamentos formados com os elementos de um conjunto serão considerados combinações simples se os elementos dos agrupamentos diferenciarem apenas pela sua natureza....
- Combinações
Combinação simples é um tipo de agrupamento no estudo sobre análise combinatória. Os agrupamentos formados com os elementos de um conjunto serão considerados combinações simples se os elementos dos agrupamentos diferenciarem apenas pela sua natureza....
- Combinações
Combinação simples é um tipo de agrupamento no estudo sobre análise combinatória. Os agrupamentos formados com os elementos de um conjunto serão considerados combinações simples se os elementos dos agrupamentos diferenciarem apenas pela sua natureza....
Matemática
Por que fatorial de zero é 1?
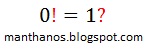
Para responder Por que fatorial de zero é 1? poderíamos simplesmente dizer (como fazem a maior parte daqueles que apresentam o conceito) que é igual a 1 por definição.
Mas há um motivo lógico para se fazer esta definição e é isto que pretendemos apresentar nesta postagem.
Em geral o conceito de fatorial aparece quando estamos a trabalhar com permutações. Ele é, a princípio, definido para números maiores do que zero:
E de um modo mais geral:
Em uma primeira vista, no contexto em que o conceito aparece, não faz sentido pensar em 0! pois como poderíamos pensar em calcular permutação de objeto nenhum?
Prosseguindo no estudo de análise combinatória deduz-se diversas fórmulas, dentre as quais figura aquela que calcula o número de combinações simples:
O termo combinação mencionado acima significa agrupamentos formados com os elementos de um determinado conjunto. A fórmula se refere ao número de agrupamentos diferentes, com p elementos cada, que se pode formar a partir de um conjunto que possui n elementos.
Assim, por exemplo, dado o conjunto de três elementos {A,B,C} podemos formar:
- 3 agrupamentos com 2 elementos cada (ou seja, combinação de 3 elementos, tomados 2 a 2 é igual a três):
AB
AC
BC
Deve-se notar que quando o assunto é combinações a ordem dos elementos não importa, ou seja, BC é o mesmo que CB.
- 3 agrupamentos com 1 elemento cada (ou seja, combinação de 3 elementos, tomados 1 a 1 é igual a três):
A
B
C
- 1 único agrupamento com 3 elementos (ou seja, combinação de 3 elementos, tomados 3 a 3 é igual a um):
ABC
Deve-se notar, como já dito, que a ordem dos elementos não importa, ou seja, ABC é o mesmo que CAB.
A fórmula acima "funciona bem" para seu "propósito original", ou seja, sempre que n > p, mas vejamos o que acontece se formos utilizá-la para o caso em que n = p:
Ora, não podemos efetuar o cálculo, pois não sabemos quanto vale 0! (pois ainda não foi definido).
Mas já vimos que a combinação de 3 elementos, tomados 3 a 3 é 1. É possível ver que este resultado vale para qualquer que seja o número de elementos do conjunto, ou seja, combinação de n elementos tomados n a n é sempre igual a 1 (de fato, quantos modos há de pegar todos os elementos de um determinado conjunto de uma única vez? Lembrando que a ordem dos elementos não importa podemos afirmar que há apenas uma maneira). Então podemos escrever:
Mas aplicando a fórmula tinhamos concluído que
Segue-se destes dois últimos resultados que: se queremos que a fórmula para o cálculo de combinação continue válida para quando n é igual a p, temos que definir 0! de modo que seja válida a seguinte igualdade:
Analise a equação acima e convença-se de que a única definição possível que preserva sua validade é:
Em matemática, ao se estender um conceito para além do campo de definição original a intenção é que todas as regras e fórmulas já conhecidas continuem válidas. Isto é o que acaba de ocorrer: define-se zero fatorial convenientemente como sendo igual a um, pois esta atitude preserva a validade de alguns resultados já conhecidos (no nosso exemplo, a validade da fórmula de combinação).
É semelhante ao que ocorre com a definição a0 = 1 discutida em postagem anterior: estender o conceito preservando a validade de resultados anteriores.
Referência:
Videoaula do PAPMEM: 23-07-10 - 10:45 - 12:00 - Professores (em particular Paulo Cezar Pinto Carvalho) - Perguntas e Respostas. Acesso em 5/4/11.
*Erros podem ser apontados aqui.
_______________________________________________________
FIQUE SABENDO OUTROS PORQUÊS:
Por que racionalizar o denominador?
Por que menos vezes menos dá mais?
Por que todo número elevado a zero dá um?
_______________________________________________________
- Combinações
Combinação simples é um tipo de agrupamento no estudo sobre análise combinatória. Os agrupamentos formados com os elementos de um conjunto serão considerados combinações simples se os elementos dos agrupamentos diferenciarem apenas pela sua natureza....
- Combinações
Seja C um conjunto com m elementos distintos. No estudo de arranjos, já vimos antes que é possível escolher p elementos de A, mas quando realizamos tais escolhas pode acontecer que duas coleções com p elementos tenham os mesmos elementos em ordens...
- Combinações
Combinação simples é um tipo de agrupamento no estudo sobre análise combinatória. Os agrupamentos formados com os elementos de um conjunto serão considerados combinações simples se os elementos dos agrupamentos diferenciarem apenas pela sua natureza....
- Combinações
Combinação simples é um tipo de agrupamento no estudo sobre análise combinatória. Os agrupamentos formados com os elementos de um conjunto serão considerados combinações simples se os elementos dos agrupamentos diferenciarem apenas pela sua natureza....
- Combinações
Combinação simples é um tipo de agrupamento no estudo sobre análise combinatória. Os agrupamentos formados com os elementos de um conjunto serão considerados combinações simples se os elementos dos agrupamentos diferenciarem apenas pela sua natureza....
