Matemática
Para verificar se a fórmula egípcia está correta temos que:
- Volume Do Tronco De Pirâmide
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Tronco De Pirâmide
Tronco de pirâmide de bases paralelas Ao cortarmos as arestas laterais de uma pirâmide por um plano semelhante à base, que não inclui esta e nem o vértice, adquirimos uma secção poligonal, onde: 1) A razão semelhança é dada pela divisão das...
- Tronco De Pirâmide
Tronco de pirâmide de bases paralelas Ao cortarmos as arestas laterais de uma pirâmide por um plano semelhante à base, que não inclui esta e nem o vértice, adquirimos uma secção poligonal, onde: 1) A razão semelhança é dada pela divisão das...
- Tronco De Pirâmide
Tronco de pirâmide de bases paralelas Ao cortarmos as arestas laterais de uma pirâmide por um plano semelhante à base, que não inclui esta e nem o vértice, adquirimos uma secção poligonal, onde: 1) A razão semelhança é dada pela divisão das...
- Volume Do Tronco De Pirâmide
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.br www.accbarrosogestar.wordpress.comwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...
Matemática
Pós-Graduação de Ensino de Ciências Exatas (UFSCAR - 2.008)
Concurso: Programa de Pós-Graduação de Ensino de Ciências Exatas ? Exame de Ingresso ? 1ª Etapa.
Ano: 2.008
Instituição: UFSCAR
Questão: 2
O problema 14 do Papiro Matemático de Moscou constitui-se no cálculo do volume de um tronco de pirâmide. Um tronco de pirâmide é o sólido resultante do corte de uma pirâmide por um plano paralelo à sua base retirando-se a pirâmide menor obtida por este corte. Se o tronco de pirâmide tem uma base quadrada de lado a, um topo quadrado de lado b, e sua altura é h, então, como perceberam os egípcios antigos, o volume do tronco de pirâmide é:
(h / 3) . (a2 + a . b + b2)
Usando o fato que o volume de uma pirâmide é (1 / 3) x área da base x altura, mostre que a fórmula egípcia para o volume do tronco de pirâmide está correta.
Solução:
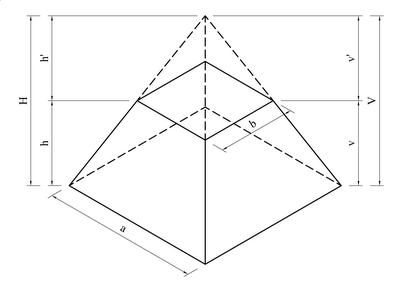
Observe a figura:

Para verificar se a fórmula egípcia está correta temos que:
- H é a altura da pirâmide original;
- h' é a altura da pirâmide retirada para formar o tronco de pirâmide;
- h é a altura do tronco de pirâmide;
- a é a medida do lado da base do tronco de pirâmide;
- b é a medida do lado do topo da pirâmide;
- V é o volume da pirâmide original;
- v' é o volume da pirâmide retirada para formar o tronco de pirâmide, e;
- v é o volume do tronco de pirâmide.
Partindo destes dados, temos:
v = V ? v?
h = H ? h? ? H = h + h?
A área da base da pirâmide original é igual a a2, e a área da base da pirâmide retirada é igual a b2.
V = (1 / 3) . a2 . H = (1 / 3) . a2 . (h + h?)
v? = (1 / 3) . b2 . h?
v = V ? v? = (1 / 3) . a2 . (h + h?) ? (1 / 3) . b2 . h? =
= (1 / 3) . [(a2 . h) + (a2 . h?) ? (b2 . h?)] = (1 / 3) . {(a2 . h) + [(a2 ? b2 ). h?]}
v = (1 / 3) . {(a2 . h) + [(a2 ? b2 ). h?]}
A pirâmide original e a pirâmide retirada são semelhantes, então tem os ângulos ordenadamente congruentes e as arestas das bases, arestas laterais, altura e demais elementos homólogos são proporcionais.
Calculando h?:
Sendo a altura da pirâmide original e da pirâmide retirada, proporcionais, calculamos a razão de proporcionalidade (k):
k = (H / h?)
A razão entre as áreas das bases é igual ao quadrado da razão de semelhança.
(a2 / b2) = k2 = (H / h?)2
(a2 / b2) = (H / h?)2 ? ?(a2 / b2) = (H / h?) ? (a / b) = (H / h?)
a . h? = H . b ? a . h? = (h + h?) . b ? a . h? = b . h + b . h?
a . h? ? b . h? = b . h
h? . (a ? b) = b . h
h? = (b . h) / (a ? b)
Substituindo h? em v, temos:
v = (1 / 3) . {(a2 . h) + [(a2 ? b2) . h?]} =
= (1 / 3) . {(a2 . h) + [(a ? b) . (a + b) . [(b . h) / (a ? b)]]} =
= (1 / 3) . {(a2 . h) + [(a + b). (b . h)]} =
= (1 / 3) . {(a2 . h) + [(a . b + b2). h]} =
= (1 / 3) . {h . (a2 + a . b + b2)} = (h / 3) . (a2 + a . b + b2)
Para saber mais, consulte:
DOLCE, Osvaldo. POMPEO, José Nicolau. Fundamentos de matemática elementar ? volume 10 ? geometria espacial: posição e métrica. 5.ed. São Paulo: Atual, 1993. p.268-278
- Volume Do Tronco De Pirâmide
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Tronco De Pirâmide
Tronco de pirâmide de bases paralelas Ao cortarmos as arestas laterais de uma pirâmide por um plano semelhante à base, que não inclui esta e nem o vértice, adquirimos uma secção poligonal, onde: 1) A razão semelhança é dada pela divisão das...
- Tronco De Pirâmide
Tronco de pirâmide de bases paralelas Ao cortarmos as arestas laterais de uma pirâmide por um plano semelhante à base, que não inclui esta e nem o vértice, adquirimos uma secção poligonal, onde: 1) A razão semelhança é dada pela divisão das...
- Tronco De Pirâmide
Tronco de pirâmide de bases paralelas Ao cortarmos as arestas laterais de uma pirâmide por um plano semelhante à base, que não inclui esta e nem o vértice, adquirimos uma secção poligonal, onde: 1) A razão semelhança é dada pela divisão das...
- Volume Do Tronco De Pirâmide
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.br www.accbarrosogestar.wordpress.comwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...
