Matemática
A terceira maneira de fatorar expressões algébricas é utilizando a regra do trinômio do quadrado perfeito. Para que possa fatorar uma expressão algébrica utilizando esse 3º caso a expressão deverá ser um trinômio e formar um quadrado perfeito.
Então, para compreender melhor esse tipo de fatoração vamos recapitular o que é um trinômio e quando um trinômio pode ser um quadrado perfeito.
Trinômio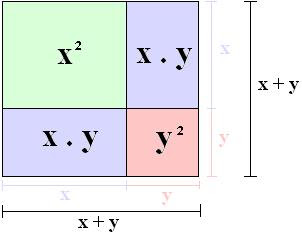
Para que uma expressão algébrica seja considerada um trinômio, ela deverá conter exatamente 3 monômios, veja alguns exemplos de trinômios:
x3 + 2x2 + 2x
- 2x5 + 5y – 5
ac + c – b
É importante ressaltar que nem todos os trinômios são quadrados perfeitos. É preciso verificar se um trinômio pode ser escrito na forma de um quadrado perfeito.
Quadrado perfeito
Veja a demonstração do que é um quadrado perfeito:
Um número é um exemplo de quadrado perfeito, basta que esse número seja o resultado de outro número elevado ao quadrado, por exemplo: 36 é um quadrado perfeito, pois
62 = 36.
Agora, para aplicar isso em uma expressão algébrica, observe o quadrado (todos os lados iguais) a abaixo com lados x + y, o valor desse lado é uma expressão algébrica.
Para calcularmos a área desse quadrado podemos seguir duas formas diferentes:
1º forma: A fórmula para o cálculo da área do quadrado é A = Lado2 , então como o lado nesse quadrado é x + y, basta elevá-lo ao quadrado.
A1 = (x + y) . (x + y) que é o mesmo que A1 = (x + y)2, então podemos dizer que:
O resultado dessa área A1 = (x + y)2 é um quadrado perfeito.
2º forma: Esse quadrado foi dividido em quatro retângulos onde cada um tem a sua própria área, então a soma de todas essas áreas é a área total do quadrado maior, ficando assim:
A2 = x2 + xy + xy + y2, como xy e xy são semelhantes podemos somá-los
A2 = x2 +2xy + y2
O resultado da área A2 = x2 +2xy + y2 é um trinômio.
As duas áreas encontradas representam a área do mesmo quadrado, então:
A1 = A2
(x + y)2 = x2 +2xy + y2
Então, o trinômio x2 +2xy + y2 tem como quadrado perfeito (x + y)2.
Quando tivermos uma expressão algébrica e ela for um trinômio do quadrado perfeito, a sua forma fatorada é representada em forma de quadrado perfeito, veja:
O trinômio x2 +2xy + y2 fatorado fica (x + y)2.
Como já foi dito, nem todos os trinômios são quadrados perfeitos, por isso é preciso que saibamos identificar se um trinômio é quadrado perfeito ou não. Veja como é feita essa identificação:
Quando um trinômio é quadrado perfeito
O quadrado perfeito (x + y)2 é composto por dois fatores (x e y) , a resolução dele é um trinômio x2 +2xy + y2, o primeiro monômio é o quadrado do primeiro termo e o segundo monômio é duas vezes o primeiro termo vezes o segundo, o terceiro monômio é o quadrado do segundo termo.
Esse trinômio do quadrado perfeito é considerado uma forma geral seguida para qualquer quadrado perfeito.
Portanto, para que um trinômio seja quadrado perfeito ele tem que seguir esse modelo. Fazendo um resumo podemos dizer que:
Para que um trinômio seja quadrado perfeito ele deve ter algumas características:
• Dois termos (monômios) do trinômio devem ser quadrados.
• Um termo (monômio) do trinômio deve ser o dobro das raízes quadradas dos dois outros termos.
Veja alguns exemplos:
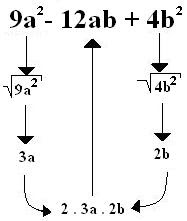
Veja se o trinômio 9a2 – 12ab + 4b2 é um quadrado perfeito, para isso siga as regras que foram citadas.
Dois membros do trinômio 9a2 – 12ab + 4b2 têm raízes quadradas e o dobro delas é o termo do meio, então o trinômio é quadrado perfeito.
Então, a forma fatorada do trinômio 9a2 – 12ab + 4b2 é (3a – 2b)2, pois é a soma das raízes ao quadrado.
Exemplo:
Dado o trinômio 4x2 – 8xy + y2, devemos tirar as raízes dos termos 4x2 e y2 , as raízes serão respectivamente 2x e y. O dobro dessas raízes deve ser 2 . 2x . y = 4xy, que é diferente do termo 8xy, então esse trinômio não poderá ser fatorado utilizando o quadrado perfeito.
- Fatoração
Fatorar uma expressão algébrica é modificar sua forma de soma algébrica para produto; fatorar uma expressão é obter outra expressão que a) seja equivalente à expressão dada; b) esteja na forma de produto. Na maioria dos casos, o resultado de...
- Trinômio De 2º Grau
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...
- Fatoração
Para fatorar expressões algébricas é necessário observar atentamente qual caso de fatoração pode ser aplicado. São sete os casos diferentes utilizados na fatoração de expressão algébricas. O primeiro caso é a fatoração por meio do termo...
- 4º Caso De Fatoração: Trinômio Do Tipo X² + Sx + P
O quarto caso de fatoração, assim como o terceiro, é a fatoração de uma expressão algébrica em forma de trinômio. A diferença dos dois é que nesse quarto caso o trinômio não tem que formar um quadrado perfeito e sim somar o produto dos dois...
- FatoraÇÃo
Fatorar é transformar equações algébricas em produtos de duas ou mais expressões, chamadas fatores. Ex: ax + ay = a.(x+y) Existem vários casos de fatoração como: 1) Fator Comum em evidênciaQuando os termos apresentam fatores comuns Observe...
Matemática
Quadrado perfeito
A terceira maneira de fatorar expressões algébricas é utilizando a regra do trinômio do quadrado perfeito. Para que possa fatorar uma expressão algébrica utilizando esse 3º caso a expressão deverá ser um trinômio e formar um quadrado perfeito.
Então, para compreender melhor esse tipo de fatoração vamos recapitular o que é um trinômio e quando um trinômio pode ser um quadrado perfeito.
Trinômio
Para que uma expressão algébrica seja considerada um trinômio, ela deverá conter exatamente 3 monômios, veja alguns exemplos de trinômios:
x3 + 2x2 + 2x
- 2x5 + 5y – 5
ac + c – b
É importante ressaltar que nem todos os trinômios são quadrados perfeitos. É preciso verificar se um trinômio pode ser escrito na forma de um quadrado perfeito.
Quadrado perfeito
Veja a demonstração do que é um quadrado perfeito:
Um número é um exemplo de quadrado perfeito, basta que esse número seja o resultado de outro número elevado ao quadrado, por exemplo: 36 é um quadrado perfeito, pois
62 = 36.
Agora, para aplicar isso em uma expressão algébrica, observe o quadrado (todos os lados iguais) a abaixo com lados x + y, o valor desse lado é uma expressão algébrica.
Para calcularmos a área desse quadrado podemos seguir duas formas diferentes:
1º forma: A fórmula para o cálculo da área do quadrado é A = Lado2 , então como o lado nesse quadrado é x + y, basta elevá-lo ao quadrado.
A1 = (x + y) . (x + y) que é o mesmo que A1 = (x + y)2, então podemos dizer que:
O resultado dessa área A1 = (x + y)2 é um quadrado perfeito.
2º forma: Esse quadrado foi dividido em quatro retângulos onde cada um tem a sua própria área, então a soma de todas essas áreas é a área total do quadrado maior, ficando assim:
A2 = x2 + xy + xy + y2, como xy e xy são semelhantes podemos somá-los
A2 = x2 +2xy + y2
O resultado da área A2 = x2 +2xy + y2 é um trinômio.
As duas áreas encontradas representam a área do mesmo quadrado, então:
A1 = A2
(x + y)2 = x2 +2xy + y2
Então, o trinômio x2 +2xy + y2 tem como quadrado perfeito (x + y)2.
Quando tivermos uma expressão algébrica e ela for um trinômio do quadrado perfeito, a sua forma fatorada é representada em forma de quadrado perfeito, veja:
O trinômio x2 +2xy + y2 fatorado fica (x + y)2.
Como já foi dito, nem todos os trinômios são quadrados perfeitos, por isso é preciso que saibamos identificar se um trinômio é quadrado perfeito ou não. Veja como é feita essa identificação:
Quando um trinômio é quadrado perfeito
O quadrado perfeito (x + y)2 é composto por dois fatores (x e y) , a resolução dele é um trinômio x2 +2xy + y2, o primeiro monômio é o quadrado do primeiro termo e o segundo monômio é duas vezes o primeiro termo vezes o segundo, o terceiro monômio é o quadrado do segundo termo.
Esse trinômio do quadrado perfeito é considerado uma forma geral seguida para qualquer quadrado perfeito.
Portanto, para que um trinômio seja quadrado perfeito ele tem que seguir esse modelo. Fazendo um resumo podemos dizer que:
Para que um trinômio seja quadrado perfeito ele deve ter algumas características:
• Dois termos (monômios) do trinômio devem ser quadrados.
• Um termo (monômio) do trinômio deve ser o dobro das raízes quadradas dos dois outros termos.
Veja alguns exemplos:
Veja se o trinômio 9a2 – 12ab + 4b2 é um quadrado perfeito, para isso siga as regras que foram citadas.
Dois membros do trinômio 9a2 – 12ab + 4b2 têm raízes quadradas e o dobro delas é o termo do meio, então o trinômio é quadrado perfeito.
Então, a forma fatorada do trinômio 9a2 – 12ab + 4b2 é (3a – 2b)2, pois é a soma das raízes ao quadrado.
Exemplo:
Dado o trinômio 4x2 – 8xy + y2, devemos tirar as raízes dos termos 4x2 e y2 , as raízes serão respectivamente 2x e y. O dobro dessas raízes deve ser 2 . 2x . y = 4xy, que é diferente do termo 8xy, então esse trinômio não poderá ser fatorado utilizando o quadrado perfeito.
- Fatoração
Fatorar uma expressão algébrica é modificar sua forma de soma algébrica para produto; fatorar uma expressão é obter outra expressão que a) seja equivalente à expressão dada; b) esteja na forma de produto. Na maioria dos casos, o resultado de...
- Trinômio De 2º Grau
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...
- Fatoração
Para fatorar expressões algébricas é necessário observar atentamente qual caso de fatoração pode ser aplicado. São sete os casos diferentes utilizados na fatoração de expressão algébricas. O primeiro caso é a fatoração por meio do termo...
- 4º Caso De Fatoração: Trinômio Do Tipo X² + Sx + P
O quarto caso de fatoração, assim como o terceiro, é a fatoração de uma expressão algébrica em forma de trinômio. A diferença dos dois é que nesse quarto caso o trinômio não tem que formar um quadrado perfeito e sim somar o produto dos dois...
- FatoraÇÃo
Fatorar é transformar equações algébricas em produtos de duas ou mais expressões, chamadas fatores. Ex: ax + ay = a.(x+y) Existem vários casos de fatoração como: 1) Fator Comum em evidênciaQuando os termos apresentam fatores comuns Observe...
