Matemática
Logo o valor decimal da raiz quadrada de dois está entre 1 e 2 e escrevemos:
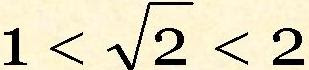
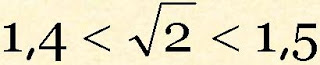
e logo sabemos que o valor decimal está entre 1,41 e 1,42 e escrevemos:
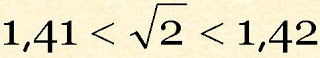
E concluímos que está entre 1,414 e 1,415 e escrevemos:
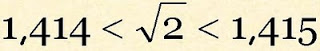
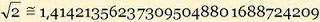Num primeiro momento e intuitivamente isso é suficiente para dizer aos estudantes da educação básica, que estamos diante de um número irracional. Mas será que isso garante a irracionalidade desse número? Não. É necessário a prova, a demonstração, as garantias que mesmo sendo um número decimal infinito em nenhum momento ele vai ter um período (Parte que se repete infinitamente) como, por exemplo, no número: 1,414444... que é um número racional pois é possível escrevê-lo na forma de fração. Então vamos lá.
Por: Profº Carlos Renato
Blog Matematicamente Contando
- Questão 70 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
A respeito do conjunto dos números reais, é verdade que (A) nem todo número racional pode ser expresso por meio de uma fração.(B) se um número tem representação decimal infinita, então esse número é racional.(C) o número 1/43 não é racional,...
- Números Decimais
NÚMEROS DECIMAIS FRAÇÃO DECIMAL Chama-se fração decimal toda fração cujo denominador é 10 ou potência de 10 ex 10, 100, 100... como: a) 7/10 b) 3/100 c) 27/1000 NÚMEROS DECIMAIS a) 7/10 = 0,7 b) 3/100 = 0,03 c) 27/1000 = 0,027 nos números decimais...
- Raiz Quadrada
Chama-se raiz quadrada de um número natural, um segundo número natural cujo o quadrado é igual ao número dado. Exemplos: a) √49 = 7 porque 7² = 49 b) √100 = 10 porque 10² = 100 NÚMEROS QUADRADOS PERFEITOS Vamos calcular os quadrados dos primeiros...
- Números Decimais
NÚMEROS DECIMAIS FRAÇÃO DECIMAL Chama-se fração decimal toda fração cujo denominador é 10 ou potência de 10 ex 10, 100, 100... como: a) 7/10 b) 3/100 c) 27/1000 NÚMEROS DECIMAIS a) 7/10 = 0,7 b) 3/100 = 0,03 c) 27/1000 = 0,027 nos números decimais...
- Conjunto
1- Naturais (IN) N = {0,1,2,3,4,5...} Convém destacar um subconjunto: N* = N - {0} = {1,2,3,4,5...} É importante lembrar que sempre é possível efetuar a adição e a multiplicação, isto é, a soma e o produto de dois números naturais sempre terá...
Matemática
Raíz de 2 - A Prova
Dizem por aí que a raiz quadrada de dois é um dos números responsáveis pela 1ª crise entre os matemáticos gregos, pois o teorema de Pitágoras garantia, na época (e garante até hoje), que esse valor é a medida da diagonal de um quadrado cujo lado mede uma unidade. Nenhum problema haveria se no século III a.C. só fossem conhecidos os números inteiros e os fracionários (hoje conhecido como racionais).
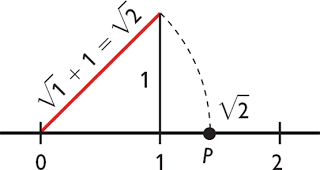
Para os pitagóricos os números regulavam o mundo (... e até então, não conseguiam dar conta de algo tão elementar: a diagonal de um quadrado.) Surge então Euclides de Alexandria e prova que a raiz quadrada de dois não é racional e, portanto existem números não-racionais. Euclides usou um raciocínio, que veremos adiante, denominado de ?redução ao absurdo?. Antes, vamos rever e calcular a raiz quadrada de 2 com aproximação decimal, já que se trata de um número irracional. Veja:
1² = 1 e 2² = 4
Logo o valor decimal da raiz quadrada de dois está entre 1 e 2 e escrevemos:
Agora vamos considerar, eventualmente, alguns valores entre 1 e 2 para elevarmos ao quadrado e chegaremos a conclusão que:
1,4² = 1,96 e 1,5² = 2,25
Logo o valor decimal está entre 1,4 e 1,5 e escrevemos:
Continuando a aproximação decimal até a 2ª casa decimal, encontraremos:
1,41² = 1,9881 e 1,42² = 2,0164
e logo sabemos que o valor decimal está entre 1,41 e 1,42 e escrevemos:
Aproximando mais ainda encontraremos como valor decimal da raiz quadrada de dois até a 3ª casa decimal:
1,414² = 1,999396 e 1,415² = 2,002225
E concluímos que está entre 1,414 e 1,415 e escrevemos:
Prosseguindo infinitamente, encontraremos a raiz quadrada aproximada de 2 com quantas casas decimais desejarmos, sem, entretanto, encontrarmos um número decimal cujo quadrado dê exatamente 2. Como curiosidade observe o valor decimal aproximado com 30 casas decimais e obtido na calculadora.
Num primeiro momento e intuitivamente isso é suficiente para dizer aos estudantes da educação básica, que estamos diante de um número irracional. Mas será que isso garante a irracionalidade desse número? Não. É necessário a prova, a demonstração, as garantias que mesmo sendo um número decimal infinito em nenhum momento ele vai ter um período (Parte que se repete infinitamente) como, por exemplo, no número: 1,414444... que é um número racional pois é possível escrevê-lo na forma de fração. Então vamos lá. Sejamos bem vindos aos irracionais.
Blog Matematicamente Contando
- Questão 70 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
A respeito do conjunto dos números reais, é verdade que (A) nem todo número racional pode ser expresso por meio de uma fração.(B) se um número tem representação decimal infinita, então esse número é racional.(C) o número 1/43 não é racional,...
- Números Decimais
NÚMEROS DECIMAIS FRAÇÃO DECIMAL Chama-se fração decimal toda fração cujo denominador é 10 ou potência de 10 ex 10, 100, 100... como: a) 7/10 b) 3/100 c) 27/1000 NÚMEROS DECIMAIS a) 7/10 = 0,7 b) 3/100 = 0,03 c) 27/1000 = 0,027 nos números decimais...
- Raiz Quadrada
Chama-se raiz quadrada de um número natural, um segundo número natural cujo o quadrado é igual ao número dado. Exemplos: a) √49 = 7 porque 7² = 49 b) √100 = 10 porque 10² = 100 NÚMEROS QUADRADOS PERFEITOS Vamos calcular os quadrados dos primeiros...
- Números Decimais
NÚMEROS DECIMAIS FRAÇÃO DECIMAL Chama-se fração decimal toda fração cujo denominador é 10 ou potência de 10 ex 10, 100, 100... como: a) 7/10 b) 3/100 c) 27/1000 NÚMEROS DECIMAIS a) 7/10 = 0,7 b) 3/100 = 0,03 c) 27/1000 = 0,027 nos números decimais...
- Conjunto
1- Naturais (IN) N = {0,1,2,3,4,5...} Convém destacar um subconjunto: N* = N - {0} = {1,2,3,4,5...} É importante lembrar que sempre é possível efetuar a adição e a multiplicação, isto é, a soma e o produto de dois números naturais sempre terá...