Matemática
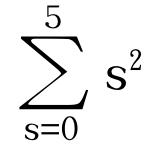
![\sum_{k=1}^{n}a_k [;\sum_{k=1}^{n}a_k;]](matematica/matematica-5631d0ea6ab68.)
Esse símbolo lê-se "a soma de![a_k [;a_k;]](matematica/matematica-5631d0ea7a5a6.) , de
, de ![k=1 [;k=1;]](matematica/matematica-5631d0ea89448.) a
a ![k=n [;k=n;]](matematica/matematica-5631d0ea98d44.) ", ou seja,
", ou seja,
![\sum_{k=1}^{n}a_k = a_1 + a_2 + \ldots + a_n [;\sum_{k=1}^{n}a_k = a_1 + a_2 + \ldots + a_n;]](matematica/matematica-5631d0ea6ab68.%20=%20a_1%20+%20a_2%20+%20%5Cldots%20+%20a_n)
Proposição 1: Valem as seguintes propriedades para somatórios:
![i) [;i);]](matematica/matematica-5631d0eabdb44.)
![\displaystyle{\sum_{k=1}^{n}}ca_k = c\displaystyle{\sum_{k=1}^{n}a_k} [;\displaystyle{\sum_{k=1}^{n}}ca_k = c\displaystyle{\sum_{k=1}^{n}a_k};]](matematica/matematica-5631d0ead2cb2.)
![ii) [;ii);]](matematica/matematica-5631d0eaf103f.)
![\displaystyle{\sum_{k=1}^{n}(a_k + b_k)} = \displaystyle{\sum_{k=1}^{n}}a_k + \displaystyle{\sum_{k=1}^{n}}b_k [;\displaystyle{\sum_{k=1}^{n}(a_k + b_k)} = \displaystyle{\sum_{k=1}^{n}}a_k + \displaystyle{\sum_{k=1}^{n}}b_k;]](matematica/matematica-5631d0eb0b8da.)
![iii) [;iii);]](matematica/matematica-5631d0eb1b37b.) Seja
Seja ![m < n [; m < n;]](matematica/matematica-5631d0eb2a172.) , então
, então![\displaystyle{\sum_{k=m}^{n}}a_k = \displaystyle{\sum_{k=1}^{n}}a_k - \displaystyle{\sum_{k = 1}^{m-1}}a_k [;\displaystyle{\sum_{k=m}^{n}}a_k = \displaystyle{\sum_{k=1}^{n}}a_k - \displaystyle{\sum_{k = 1}^{m-1}}a_k;]](matematica/matematica-5631d0eb70fe3.)
![iv) [;iv);]](matematica/matematica-5631d0eb807c7.)
![\displaystyle{\sum_{k=1}^{n}}1 = n [;\displaystyle{\sum_{k=1}^{n}}1 = n;]](matematica/matematica-5631d0eb95832.)
Demonstração:
![i) [;i);]](matematica/matematica-5631d0eabdb44.) De fato,
De fato,
![\sum_{k=1}^{n}ca_k = ca_1 + ca_2 + \ldots + ca_n = c(a_1 + a_2 + \ldots + a_n) = c\sum_{k=1}^{n}a_k [;\sum_{k=1}^{n}ca_k = ca_1 + ca_2 + \ldots + ca_n = c(a_1 + a_2 + \ldots + a_n) = c\sum_{k=1}^{n}a_k;]](matematica/matematica-5631d0ebba371.)
![ii) [;ii);]](matematica/matematica-5631d0eaf103f.) De fato,
De fato,
![\sum_{k=1}^{n}(a_k + b_k) = (a_1 + b_1) + (a_2 + b_2) + \ldots + (a_n + b_n) [;\sum_{k=1}^{n}(a_k + b_k) = (a_1 + b_1) + (a_2 + b_2) + \ldots + (a_n + b_n);]](matematica/matematica-5631d0ebd922b.)
![= (a_1 + a_2 + \ldots + a_n) + (b_1 + b_2 + \ldots + b_n) [;= (a_1 + a_2 + \ldots + a_n) + (b_1 + b_2 + \ldots + b_n);]](matematica/matematica-5631d0ebe827e.)
![=\sum_{k=1}^{n}a_k + \sum_{k=1}^{n}b_k [;=\sum_{k=1}^{n}a_k + \sum_{k=1}^{n}b_k;]](matematica/matematica-5631d0ec09fef.)
![iii) [;iii);]](matematica/matematica-5631d0eb1b37b.) Basta notar que
Basta notar que
![\sum_{k=1}^{m-1}a_k + \sum_{k=m}^{n}a_k = \sum_{k=1}^{n}a_k [;\sum_{k=1}^{m-1}a_k + \sum_{k=m}^{n}a_k = \sum_{k=1}^{n}a_k;]](matematica/matematica-5631d0ec2dce7.)
![iv) [;iv);]](matematica/matematica-5631d0eb807c7.) Segue direto da definição de multiplicação.
Segue direto da definição de multiplicação.
Proposição 2:
![i) [;i);]](matematica/matematica-5631d0eabdb44.)
![\displaystyle{\sum_{k=1}^{n}}k = \frac{n(n+1)}{2} [;\displaystyle{\sum_{k=1}^{n}}k = \frac{n(n+1)}{2};]](matematica/matematica-5631d0ec5abe6.)
![ii) [;ii);]](matematica/matematica-5631d0eaf103f.)
![\sum_{k=1}^{n}k^2 = \frac{n(n+1)(2n+1)}{6} [;\sum_{k=1}^{n}k^2 = \frac{n(n+1)(2n+1)}{6};]](matematica/matematica-5631d0ec7fe3a.)
![\sum_{k=1}^{m+1}k = \sum_{k=1}^{m}k + (m+1) = \frac{m(m+1)}{2} + (m+1) [;\sum_{k=1}^{m+1}k = \sum_{k=1}^{m}k + (m+1) = \frac{m(m+1)}{2} + (m+1);]](matematica/matematica-5631d0ed089ff.)
![= \frac{m(m+1) + 2(m+ 1)}{2} = \frac{(m + 1)(m + 2)}{2} [;= \frac{m(m+1) + 2(m+ 1)}{2} = \frac{(m + 1)(m + 2)}{2};]](matematica/matematica-5631d0ed1e3e1.)
Outra forma de provar este resultado é usando o teorema das colunas.
![{p \choose p} + {p+1 \choose p} + \ldots + {n \choose p} = {n+1 \choose p+1} \quad \quad \text{ou} \quad \quad \sum_{k=p}^{n} {k \choose p} = {n+1 \choose p+1} [;{p \choose p} + {p+1 \choose p} + \ldots + {n \choose p} = {n+1 \choose p+1} \quad \quad \text{ou} \quad \quad \sum_{k=p}^{n} {k \choose p} = {n+1 \choose p+1};]](matematica/matematica-5631d0ed76864.)
Demonstração: Usaremos indução finita sobre![n [;n;]](matematica/matematica-5631d0ed430a2.) . Se
. Se ![n = p [;n = p;]](matematica/matematica-5631d0ed430a2.%20=%20p) , temos:
, temos:
![{p \choose p} = 1 = {p + 1 \choose p + 1} [;{p \choose p} = 1 = {p + 1 \choose p + 1};]](matematica/matematica-5631d0edb013e.)
Suponhamos que
![\sum_{k = p}^{n}{k \choose p} = {n + 1 \choose p + 1} \quad \quad \quad (2) [;\sum_{k = p}^{n}{k \choose p} = {n + 1 \choose p + 1} \quad \quad \quad (2);]](matematica/matematica-5631d0edbfaba.)
Assim,
![\sum_{k = p}^{n+1}{k \choose p} = \sum_{k = p}^{n}{k \choose p} + {n+1 \choose p+1} = {n+1 \choose p+1} + {n+1 \choose p} = {n+1 \choose p+1} [;\sum_{k = p}^{n+1}{k \choose p} = \sum_{k = p}^{n}{k \choose p} + {n+1 \choose p+1} = {n+1 \choose p+1} + {n+1 \choose p} = {n+1 \choose p+1};]](matematica/matematica-5631d0edce0cd.)
No caso particular em que![p = 1 [;p = 1;]](matematica/matematica-5631d0ed33410.%20=%201) , temos
, temos
![\sum_{k=1}^{n} {k \choose 1} = \sum_{k=1}^{n} k = {n+1 \choose 2} = \frac{(n+1)n}{2} [; \sum_{k=1}^{n} {k \choose 1} = \sum_{k=1}^{n} k = {n+1 \choose 2} = \frac{(n+1)n}{2};]](matematica/matematica-5631d0edf34c9.)
que é a soma dos números naturais de![1 [;1;]](matematica/matematica-5631d0ee145af.) a
a ![n [;n;]](matematica/matematica-5631d0ed430a2.) .
.
- Os Naturais E O Princípio Da Boa Ordenação
Autor: Blog Fatos Matemáticos - Profº Paulo Sergio Enquanto a geometria, anos antes de Cristo, nos Elementos de Euclides, já recebia um tratamento lógico-dedutivo, com seus postulados e axiomas,...
- O Corpo Dos Números Complexos - Parte Ii
Hoje daremos continuidade ao artigo enviado pelo leitor João (Portugal), quem não viu a primeira parte pode clicar aqui e ver! Segue o artigo enviando pelo João:__________________________________________________________ Antes de continuar o meu artigo...
- Progressão Geométrica (p.g.) E (pa)
Progressões Geométricas (PG) Definição Uma progressão geométrica (PG) é uma sequência numérica em que cada termo, a partir do segundo, é igual ao antecessor multiplicado por uma constante q denominada a razão da PG. Ou seja: an = an-1.q...
- Binômio De Newton
O binômio de Newton é uma maneira de expressar o desenvolvimento de um binômio na forma (a + b)n, com "n" natural.(a + b)0 = 1 (a + b)1 = a + b (a + b)2 = a2 + 2 . a . b + b2 (a + b)3 = a3 + 3 . a2 . b...
- Princípio De Indução Completa Ou Raciocínio Por Recorrência
Se uma propriedade é verdadeira para o número $1$ e conseguimos demonstrar que é verdadeira para $n$ sempre que for verdadeira para $n-1$ então ela será verdadeira para todos os números naturais.Vamos demonstrar que a soma dos $n$ primeiros...
Matemática
A Notação Sigma para Somatórios
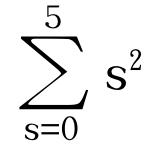
Autor: Blog Fatos Matemáticos. Profº Paulo Sergio
Para tornar clara a discussão sobre integrais definidas, é importante introduzir aqui uma notação matemática padrão usada para abreviar grandes somas. Esta é chamada "notação sigma" ou somatórios, porque utiliza a letra grega (sigma). Assim, se ![a_1,a_2,\ldots, a_n [;a_1,a_2,\ldots, a_n;]](matematica/matematica-5631d0ea5b745.) são números dados, sua soma é denotada por
são números dados, sua soma é denotada por
Esse símbolo lê-se "a soma de
Proposição 1: Valem as seguintes propriedades para somatórios:
para todo ![c \in \mathbb{R} [;c \in \mathbb{R};]](matematica/matematica-5631d0eae1bc1.) .
.
Proposição 2:
Demonstração:
![i) [;i);]](matematica/matematica-5631d0eabdb44.) Usaremos indução finita. Para
Usaremos indução finita. Para ![n=1 [;n=1;]](matematica/matematica-5631d0ec9e5c0.) , temos:
, temos:
![\sum_{k=1}^{1}k = 1 = \frac{1(1 + 1)}{2} [;\sum_{k=1}^{1}k = 1 = \frac{1(1 + 1)}{2};]](matematica/matematica-5631d0ecb4024.)
Suponhamos que a expressão é válida para![n = m [;n = m;]](matematica/matematica-5631d0ecc9153.) , ou seja, a hipótese de indução é dada por:
, ou seja, a hipótese de indução é dada por:
![\sum_{k=1}^{m}k = \frac{m(m+1)}{2} [;\sum_{k=1}^{m}k = \frac{m(m+1)}{2};]](matematica/matematica-5631d0ecdef41.)
Mostraremos que![\sum_{k=1}^{m + 1}k = \frac{(m+1)(m+2)}{2} [;\sum_{k=1}^{m + 1}k = \frac{(m+1)(m+2)}{2};]](matematica/matematica-5631d0ecee544.)
Suponhamos que a expressão é válida para
De fato,
Outra forma de provar este resultado é usando o teorema das colunas.
(Teorema das Colunas) A soma dos coeficientes binomiais situados na ![p [;p;]](matematica/matematica-5631d0ed33410.) -ésima coluna até a linha
-ésima coluna até a linha ![n [;n;]](matematica/matematica-5631d0ed430a2.) é igual ao co eficiente binomial situado na
é igual ao co eficiente binomial situado na ![(n+1) [;(n+1);]](matematica/matematica-5631d0ed51c25.) -ésima linha e
-ésima linha e ![(p+1) [;(p+1);]](matematica/matematica-5631d0ed613bf.) -ésima coluna, ou seja:
-ésima coluna, ou seja:
Demonstração: Usaremos indução finita sobre
Suponhamos que
Assim,
No caso particular em que
que é a soma dos números naturais de
- Os Naturais E O Princípio Da Boa Ordenação
Autor: Blog Fatos Matemáticos - Profº Paulo Sergio Enquanto a geometria, anos antes de Cristo, nos Elementos de Euclides, já recebia um tratamento lógico-dedutivo, com seus postulados e axiomas,...
- O Corpo Dos Números Complexos - Parte Ii
Hoje daremos continuidade ao artigo enviado pelo leitor João (Portugal), quem não viu a primeira parte pode clicar aqui e ver! Segue o artigo enviando pelo João:__________________________________________________________ Antes de continuar o meu artigo...
- Progressão Geométrica (p.g.) E (pa)
Progressões Geométricas (PG) Definição Uma progressão geométrica (PG) é uma sequência numérica em que cada termo, a partir do segundo, é igual ao antecessor multiplicado por uma constante q denominada a razão da PG. Ou seja: an = an-1.q...
- Binômio De Newton
O binômio de Newton é uma maneira de expressar o desenvolvimento de um binômio na forma (a + b)n, com "n" natural.(a + b)0 = 1 (a + b)1 = a + b (a + b)2 = a2 + 2 . a . b + b2 (a + b)3 = a3 + 3 . a2 . b...
- Princípio De Indução Completa Ou Raciocínio Por Recorrência
Se uma propriedade é verdadeira para o número $1$ e conseguimos demonstrar que é verdadeira para $n$ sempre que for verdadeira para $n-1$ então ela será verdadeira para todos os números naturais.Vamos demonstrar que a soma dos $n$ primeiros...
