Matemática
Demonstração:
c+b=\frac{a^2}{c-b}
\end{equation}
S_1: \left\{\begin{matrix}
c & -&b & =&a^2\\
c & +&b & =&1
\end{matrix}\right.
\qquad
S_2:\left\{\begin{matrix}
c & -&b & =&a\\
c & +&b & =&a
\end{matrix}\right.
\qquad
S_3:\left\{\begin{matrix}
c & -&b & =&1\\
c & +&b & =&a^2
\end{matrix}\right.
\end{equation}
c=\frac{a^2+1}{2} \qquad \text{,}\qquad b=c-1
\end{equation}
Exemplos:
$1)$ Se $a=3$, $\displaystyle c=\frac{3^2+1}{2}=5$ e $b=c-1=5-1=4$
O terno pitagórico é: $(a,b,c)=(3,4,5)$.
$2)$ Se $a=5$, $\displaystyle c=\frac{5^2+1}{2}=13$ e $b=13-1=12$.
O terno pitagórico é: $(a,b,c)=(5,12,13)$.
$3)$ Se $a=13$, $\displaystyle c=\frac{13^2+1}{2}=85$ e $b=85-1=84$.
O terno pitagórico é: $(a,b,c)=(13,84,85)$.
Como $c=85$ é um ímpar composto, o teorema $1$ falha e este caso será analisado no teorema $4$.
Teorema $2$: Se $a<b<c$ forem inteiros, então a equação $a^2+b^2=c^2$ tem apenas uma solução se $a$ for um par da forma $2p$, onde $p$ é um primo ímpar;
Demonstração:
Substituindo $a$ por $2p$ na equação $(1)$, obtemos:
\begin{equation}
c+b=\frac{4p^2}{c-b}
\end{equation}
Como $c$ e $b$ são inteiros, $c-b$ tem que dividir $4p^2$ sem deixar resto; logo, $c-b$ são os divisores positivos de $4p^2$ menores que $4p$. Os divisores pares de $4p^2$ menores que $4p$ são: $2$ e $4$. Substituindo $2$ e $4$ por $c-b$ em $\displaystyle c+b=\frac{4p^2}{c-b}$, obtemos os seguintes sistemas lineares:
\begin{equation}
S_1: \left\{\begin{matrix}
c & -&b & =&2\\
c & +&b & =&2p^2
\end{matrix}\right.
\qquad
S_2:\left\{\begin{matrix}
c & -&b & =&4\\
c & +&b & =&p^2
\end{matrix}\right.
\end{equation}
Já que $c$ é inteiro, dos sistemas de equações acima somente $S_1$ é compatível. Resolvendo $S_1$, obtemos:
\begin{equation}
c=p^2+1
\end{equation}
Como $a=2p$, logo $\displaystyle p=\frac{a}{2}$. Substituindo $p$ por $\displaystyle \frac{a}{2}$ na relação $(6)$, obtemos que:
\begin{equation}
c=\frac{a^2}{4}+1 \qquad \text{,} \qquad b=c-2
\end{equation}
Exemplos:
$4)$ Se $a=2p=2\cdot 3=6$, $\displaystyle c=\frac{6^2}{4}+1=10$ e $b=10-2=8$.
O triângulo pitagórico: $(a,b,c)=(6,8,10)$.
$5)$ Se $a=2p=2\cdot 5=10$, $\displaystyle c=\frac{10^2}{4}+1=26$ e $b=26-2=24$.
O triângulo pitagórico: $(a,b,c)=(10, 24, 26)$.
$6)$ Se $a=2p=2\cdot13=26$, $\displaystyle c=\frac{26^2}{4}+1=170$ e $b=170-2=168$.
O triângulo pitagórico: $(a,b,c)=(26, 168, 170)$.
Como $c=170$ não é um par da forma $2p$, o teorema $2$ falha e este caso será analisado no teorema $3$.
Demonstração:
S_1: \left\{\begin{matrix}
c & -&b & =&k\\
c & +&b & =&\frac{a^2}{k}
\end{matrix}\right.
\end{equation}
Resolvendo o sistema de equações acima, obtemos a seguinte solução:
\begin{equation}
2c=k+\frac{a^2}{k}\qquad \text{ou}\qquad c=\frac{a^2+k^2}{2k}
\end{equation}
Exemplos:
Para $a=170$ e $k=2$, temos:$\displaystyle \frac{170^2}{2\cdot 1}=7225$;
Para $a=170$ e $k=4$, temos: $\displaystyle \frac{170^2}{2\cdot 4}=3612,5$;
Para $a=170$ e $k=10$, temos: $\displaystyle \frac{170^2}{2\cdot 10}=1445$;
Para $a=170$ e $k=20$, temos: $\displaystyle \frac{170^2}{2 \cdot 20}=722,5$;
Para $a=170$ e $k=34$, temos: $\displaystyle \frac{170^2}{2\cdot 34}=425$;
Para $=170$ e $k=50$, temos: $\displaystyle \frac{170^2}{2\cdot 50}=289$;
Para $a=170$ e $k=64$, temos: $\displaystyle \frac{170^2}{2\cdot 64}=212,5$.
$(170, 7224, 7226)$, $(170, 1440, 1450)$, $(170, 408, 442)$ e $(170, 264, 314)$.
Os divisores pares de $314^2 < 314$ são $k=2$ e $k=4$.
Para $a=314$ e $k=2$, temos: $\displaystyle \frac{314^2}{2\cdot 2}=24649$;
Para $a=314$ e $k=4$, temos: $\displaystyle \frac{314^2}{2\cdot 4}=12324,5$.
Só existe um terno pitagórico com $a=314$. Para $a=314$ e $k=2$, o terno pitagórico é:
\begin{equation*}
c=\frac{314^2+2^2}{2\cdot 2}=24650 \qquad \text{e} \qquad b=24650-2-25648
\end{equation*}
O triângulo pitagórico é $(a,b,c)=(314, 24648, 24650)$.
Demonstração:
Exemplos:
$8)$ Os divisores de $85^2<85$ são: $k=1$, $k=5$, $k=17$ e $k=25$.
Para $k=1$:
\begin{equation*}
c=\frac{85^2+1^1}{2\cdot 1}=3613 \qquad \text{e} \qquad b=3613-1=3612
\end{equation*}
O triângulo pitagórico: $(a,b,c)=(85, 3612,3613)$.
Para $k=5$:
\begin{equation*}
c=\frac{85^2+5^2}{2\cdot 5}=725 \qquad \text{e} \qquad b=725-5=720
\end{equation*}
O triângulo pitagórico: $(a,b,c)=(85, 720,725)$.
Para $k=17$:
\begin{equation*}
c=\frac{85^2+17^2}{2\cdot 17}=221 \qquad \text{2} \qquad b=221-17=204
\end{equation*}
O triângulo pitagórico: $(a,b,c)=(85, 204, 221)$.
Para $k=25$:
\begin{equation*}
c=\frac{85^2+25^2}{2\cdot 25}=157 \qquad \text{e} \qquad b=157-25=132
\end{equation*}
O triângulo pitagórico $(a,b,c)=(85, 132, 157)$.
O divisor de $157^2 < 157$ é: $k=1$
Para $k=1$:
\begin{equation*}
c=\frac{157^2+1^2}{2\cdot 1}=12325 \qquad \text{e} \qquad b=12325-1=12324
\end{equation*}
Para $k=10625$:
\begin{equation*}
c=\frac{12325^2+10625^2}{2\cdot 10625}=12461 \qquad \text{e} \qquad b=12461-10625=1836
\end{equation*}
c=\frac{12325^2+7225^2}{2\cdot 7225}=14125 \qquad \text{e} \qquad b=14125-7225=6900
\end{equation*}
c=\frac{12325^2+3625^2}{2\cdot 3625}=22765 \qquad \text{e} \qquad b=22765-3625=19140
\end{equation*}
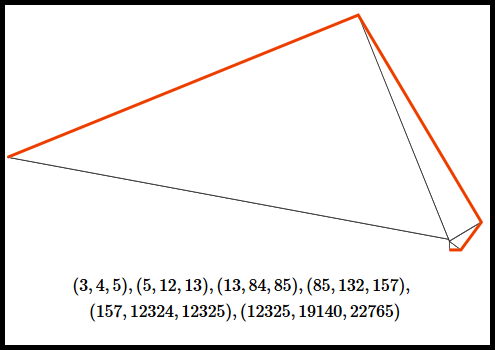
(3,4,5),(5,12,13),(13,84,85),(85,132,157),(157,12324,12325),(12325,19140,22765)
\end{equation*}
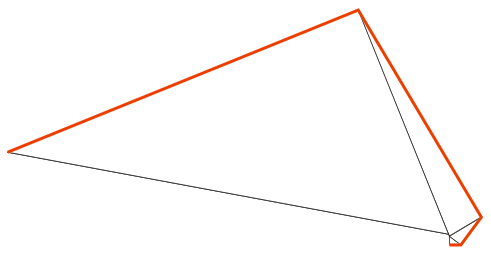
(6,8,10), (10,24,26), (26,168,170), (170, 264, 314), (314, 24648, 24650)
\end{equation*}
Este artigo foi cedido gentilmente por Sebastião Vieira do Nascimento (Sebá). Professor Titular (por concurso) aposentado da UFCG – PB, além de colaborador deste blog. Foram feitas algumas alterações do manuscrito original para melhor exposição.
Construindo Raízes de Números Naturais
Construção da Espiral de Arquimedes com Régua e Compasso
Ternos Pitagóricos: A Tábua de Plimpton 322

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a^2}dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a^2}\ dx = \frac{1}{a}\text{arctg}\left(\frac{x}{a}\right) + C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2 + a^2 \neq 0$. Seja a integral:...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral Indefinida Do Produto De Cossenos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation} \int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
Matemática
Como Construir uma Espiral Pitagórica
A Espiral Pitagórica é construída com triângulos retângulos cujas medidas dos lados são expressas por números inteiros.
Veremos neste post sua construção, assim como o desenvolvimento das fórmulas que geram os lados dos triângulos.

A Espiral Pitagórica é construída utilizando triângulos retângulos, onde a hipotenusa do primeiro triângulo retângulo é o menor cateto do segundo; e a hipotenusa do segundo triângulo retângulo é o menor cateto do terceiro; e assim por diante. Faz-se necessário encontrarmos um algoritmo que nos dê as medidas desses triângulos para que possamos sem dificuldades, construir a espiral.
Dentre as formas analisadas para a construção, podemos encontrar $4$ possibilidades que nos levam a quatro teoremas que nos dão as fórmulas para calcularmos os lados dos triângulos retângulos que compõem a Espiral Pitagórica.
Teorema 1: Se $a<b<c$ forem inteiros, então a equação $a^2+b^2=c^2$ tem apenas uma solução se $a$ for um primo ímpar;
Demonstração:
A equação $a^2+b^2=c^2$ pode ser escrita como:
\begin{equation}c+b=\frac{a^2}{c-b}
\end{equation}
Uma vez que $b$ e $c$ são inteiros, logo $c-b$ tem que dividir $a^2$ sem deixar resto. Logo, $c-b$ são os divisores positivos de $a^2$. Se $a^2$ é o quadrado de um primo ímpar, os divisores de $a^2$ são: $a^2$, $a$ e $1$. Substituindo estes divisores na relação $(1)$, obtemos os seguintes sistemas lineares:
\begin{equation}S_1: \left\{\begin{matrix}
c & -&b & =&a^2\\
c & +&b & =&1
\end{matrix}\right.
\qquad
S_2:\left\{\begin{matrix}
c & -&b & =&a\\
c & +&b & =&a
\end{matrix}\right.
\qquad
S_3:\left\{\begin{matrix}
c & -&b & =&1\\
c & +&b & =&a^2
\end{matrix}\right.
\end{equation}
Dos três sistemas de equação acima, apenas a solução $S_3$ é compatível. Resolvendo o sistema, obtemos:
\begin{equation}c=\frac{a^2+1}{2} \qquad \text{,}\qquad b=c-1
\end{equation}
Exemplos:
$1)$ Se $a=3$, $\displaystyle c=\frac{3^2+1}{2}=5$ e $b=c-1=5-1=4$
O terno pitagórico é: $(a,b,c)=(3,4,5)$.
$2)$ Se $a=5$, $\displaystyle c=\frac{5^2+1}{2}=13$ e $b=13-1=12$.
O terno pitagórico é: $(a,b,c)=(5,12,13)$.
$3)$ Se $a=13$, $\displaystyle c=\frac{13^2+1}{2}=85$ e $b=85-1=84$.
O terno pitagórico é: $(a,b,c)=(13,84,85)$.
Como $c=85$ é um ímpar composto, o teorema $1$ falha e este caso será analisado no teorema $4$.
Teorema $2$: Se $a<b<c$ forem inteiros, então a equação $a^2+b^2=c^2$ tem apenas uma solução se $a$ for um par da forma $2p$, onde $p$ é um primo ímpar;
Demonstração:
Substituindo $a$ por $2p$ na equação $(1)$, obtemos:
\begin{equation}
c+b=\frac{4p^2}{c-b}
\end{equation}
Como $c$ e $b$ são inteiros, $c-b$ tem que dividir $4p^2$ sem deixar resto; logo, $c-b$ são os divisores positivos de $4p^2$ menores que $4p$. Os divisores pares de $4p^2$ menores que $4p$ são: $2$ e $4$. Substituindo $2$ e $4$ por $c-b$ em $\displaystyle c+b=\frac{4p^2}{c-b}$, obtemos os seguintes sistemas lineares:
\begin{equation}
S_1: \left\{\begin{matrix}
c & -&b & =&2\\
c & +&b & =&2p^2
\end{matrix}\right.
\qquad
S_2:\left\{\begin{matrix}
c & -&b & =&4\\
c & +&b & =&p^2
\end{matrix}\right.
\end{equation}
Já que $c$ é inteiro, dos sistemas de equações acima somente $S_1$ é compatível. Resolvendo $S_1$, obtemos:
\begin{equation}
c=p^2+1
\end{equation}
Como $a=2p$, logo $\displaystyle p=\frac{a}{2}$. Substituindo $p$ por $\displaystyle \frac{a}{2}$ na relação $(6)$, obtemos que:
\begin{equation}
c=\frac{a^2}{4}+1 \qquad \text{,} \qquad b=c-2
\end{equation}
Exemplos:
$4)$ Se $a=2p=2\cdot 3=6$, $\displaystyle c=\frac{6^2}{4}+1=10$ e $b=10-2=8$.
O triângulo pitagórico: $(a,b,c)=(6,8,10)$.
$5)$ Se $a=2p=2\cdot 5=10$, $\displaystyle c=\frac{10^2}{4}+1=26$ e $b=26-2=24$.
O triângulo pitagórico: $(a,b,c)=(10, 24, 26)$.
$6)$ Se $a=2p=2\cdot13=26$, $\displaystyle c=\frac{26^2}{4}+1=170$ e $b=170-2=168$.
O triângulo pitagórico: $(a,b,c)=(26, 168, 170)$.
Como $c=170$ não é um par da forma $2p$, o teorema $2$ falha e este caso será analisado no teorema $3$.
Teorema $3$: Se $a<b<c$ forem inteiros, então a equação $a^2+b^2=c^2$, possui um número de soluções inteiras igual ao número de divisores pares $(k)$ de $a^2$ menores que $a$ tal que $a^2$ divida $2k$ sem deixar resto, se $a$ for um par diferente de $2p$.
Demonstração:
Seja $c-b=k$ os divisores de $a^2$. Substituindo $c-b$ por $k$ na equação $(1)$, obtemos o seguinte sistema de equações:
\begin{equation}S_1: \left\{\begin{matrix}
c & -&b & =&k\\
c & +&b & =&\frac{a^2}{k}
\end{matrix}\right.
\end{equation}
Resolvendo o sistema de equações acima, obtemos a seguinte solução:
\begin{equation}
2c=k+\frac{a^2}{k}\qquad \text{ou}\qquad c=\frac{a^2+k^2}{2k}
\end{equation}
Como $c-b=k$, logo $b=c-k$. Como $2c$ e $k$ são sempre pares, a fim de que $c$ seja inteiro, $\displaystyle \frac{a^2}{k}$ tem que ser par. Como $2k$ e $a^2$ são pares, e além disso, $k$ são os divisores de $a^2$, se incluirmos os divisores ímpares de $a^2$, a soma $a^2+k^2$ vai ser ímpar, e, consequentemente, $a^2+k^2$ dividido por $2k$ vai ser fracionário. Foi por isso que consideramos somente os divisores pares de $a^2$.
Se $k=a$, então $\displaystyle c=\frac{a^2+a^2}{2a}=a$. Como $b=c-k$, então $b=a-a=0$. Logo, os divisores pares de $a^2$ devem ser menores que $a$.
Portanto, se $a$ for par diferente de $2p$, o número de soluções em inteiros é igual ao número de divisores pares de $a^2$ menores que $a$, que divide $\displaystyle \frac{a^2}{2k}$.
Exemplos:
$7)$ Os divisores pares de $170^2$ menores que $170$ são: $k=2$, $4$, $10$, $20$, $34$, $50$ e $68$.
Para $a=170$ e $k=2$, temos:$\displaystyle \frac{170^2}{2\cdot 1}=7225$;
Para $a=170$ e $k=4$, temos: $\displaystyle \frac{170^2}{2\cdot 4}=3612,5$;
Para $a=170$ e $k=10$, temos: $\displaystyle \frac{170^2}{2\cdot 10}=1445$;
Para $a=170$ e $k=20$, temos: $\displaystyle \frac{170^2}{2 \cdot 20}=722,5$;
Para $a=170$ e $k=34$, temos: $\displaystyle \frac{170^2}{2\cdot 34}=425$;
Para $=170$ e $k=50$, temos: $\displaystyle \frac{170^2}{2\cdot 50}=289$;
Para $a=170$ e $k=64$, temos: $\displaystyle \frac{170^2}{2\cdot 64}=212,5$.
Como para $k=4$, $k=20$ e $k=68$, $\displaystyle \frac{a^2}{2k}$ não é inteiro, logo, só existem quatro ternos pitagóricos com $a=170$, os quais são:
$(170, 7224, 7226)$, $(170, 1440, 1450)$, $(170, 408, 442)$ e $(170, 264, 314)$.
Vamos escolher a hipotenusa com menor valor como cateto menor do próximo triângulo pitagórico. Escolhemos a hipotenusa com menor valor para evitar que não trabalhemos com números muito grandes para hipotenusas.
Os divisores pares de $314^2 < 314$ são $k=2$ e $k=4$.
Para $a=314$ e $k=2$, temos: $\displaystyle \frac{314^2}{2\cdot 2}=24649$;
Para $a=314$ e $k=4$, temos: $\displaystyle \frac{314^2}{2\cdot 4}=12324,5$.
Só existe um terno pitagórico com $a=314$. Para $a=314$ e $k=2$, o terno pitagórico é:
\begin{equation*}
c=\frac{314^2+2^2}{2\cdot 2}=24650 \qquad \text{e} \qquad b=24650-2-25648
\end{equation*}
O triângulo pitagórico é $(a,b,c)=(314, 24648, 24650)$.
Como o valor da hipotenusa $(24650)$ é muito grande, paremos por aqui.
Teorema $4$: Se $a<b<c$ forem inteiros, então a equação $a^2+b^2=c^2$ possui um número de soluções igual ao número de divisores de $k$ de $a^2$ menores que $a$.
Demonstração:
Pelo Teorema $3$, já que um número ímpar composto tem apenas divisores ímpares, então se $a$ for ímpar, o número de soluções inteiras é igual ao número de divisores de $a^2$ menores que $a$.
Exemplos:
$8)$ Os divisores de $85^2<85$ são: $k=1$, $k=5$, $k=17$ e $k=25$.
Para $k=1$:
\begin{equation*}
c=\frac{85^2+1^1}{2\cdot 1}=3613 \qquad \text{e} \qquad b=3613-1=3612
\end{equation*}
O triângulo pitagórico: $(a,b,c)=(85, 3612,3613)$.
Para $k=5$:
\begin{equation*}
c=\frac{85^2+5^2}{2\cdot 5}=725 \qquad \text{e} \qquad b=725-5=720
\end{equation*}
O triângulo pitagórico: $(a,b,c)=(85, 720,725)$.
Para $k=17$:
\begin{equation*}
c=\frac{85^2+17^2}{2\cdot 17}=221 \qquad \text{2} \qquad b=221-17=204
\end{equation*}
O triângulo pitagórico: $(a,b,c)=(85, 204, 221)$.
Para $k=25$:
\begin{equation*}
c=\frac{85^2+25^2}{2\cdot 25}=157 \qquad \text{e} \qquad b=157-25=132
\end{equation*}
O triângulo pitagórico $(a,b,c)=(85, 132, 157)$.
Já que na espiral pitagórica, a partir do segundo triângulo pitagórico, o cateto menor é sempre a hipotenusa do triângulo anterior, das quatro hipotenusas $(3613, 725, 221, 157)$, vamos escolher a hipotenusa com menor valor como cateto menor do próximo triângulo pitagórico. Escolhemos a hipotenusa com menor valor para evitar que trabalhemos com números muito grandes para a hipotenusa.
O divisor de $157^2 < 157$ é: $k=1$
Para $k=1$:
\begin{equation*}
c=\frac{157^2+1^2}{2\cdot 1}=12325 \qquad \text{e} \qquad b=12325-1=12324
\end{equation*}
O triângulo pitagórico: $(a,b,c)=(157, 12324, 12325)$.
Os divisores de $12325^2 < 12325$ são:
$k=1, 5, 17, 25, 29, 85, 125, 289, 425, 493, 625, 725, 841, 1445, 2125, 2465, 3625, 7225 \: \text{e}\: 10625$.
Quanto maior o valor de $k$, menor será a medida da hipotenusa. Para evitar cálculos desnecessário, tomemos o maior valor de $k$:
Para $k=10625$:
\begin{equation*}
c=\frac{12325^2+10625^2}{2\cdot 10625}=12461 \qquad \text{e} \qquad b=12461-10625=1836
\end{equation*}
O terno pitagórico: $(a,b,c)=(12325, 1836, 12461)$. Como $b<a$, logo $(12325,1836,12461)$ é um terno pitagórico, mas não são medidas de um triângulo pitagórico.
Como para $k=10625$ não é compatível com as medidas de um triângulo pitagórico, então vamos escolher $k=7225$:
\begin{equation*}c=\frac{12325^2+7225^2}{2\cdot 7225}=14125 \qquad \text{e} \qquad b=14125-7225=6900
\end{equation*}
O terno pitagórico: $(a,b,c)=(12325, 6900, 14125)$. Como $b<a$, logo $(12325, 6900, 14125)$ é um terno pitagórico, mas não são medidas de um triângulo pitagórico.
Como para $k=7225$ não é compatível com as medidas de um triângulo pitagórico, então vamos escolher $k=3625$:
\begin{equation*}c=\frac{12325^2+3625^2}{2\cdot 3625}=22765 \qquad \text{e} \qquad b=22765-3625=19140
\end{equation*}
O triângulo pitagórico: $(a,b,c)=(12325, 19140, 22765)$.
Como o valor da hipotenusa $(22765)$ é muito grande, paramos por aqui.
Com posse dos valores encontrados nos exemplos dos teoremas $1$ a $4$ acima, podemos construir duas espirais distintas:
A primeira espiral será construída com triângulos pitagóricos, cujas hipotenusas são número ímpares, encontradas nos Teoremas $1$ e $4$:
\begin{equation*}(3,4,5),(5,12,13),(13,84,85),(85,132,157),(157,12324,12325),(12325,19140,22765)
\end{equation*}

[Espiral Pitagórica Ímpar]
A segunda espiral será construída com triângulos pitagóricos, cujas hipotenusas são pares, encontradas nos Teoremas $2$ e $3$:
\begin{equation*}(6,8,10), (10,24,26), (26,168,170), (170, 264, 314), (314, 24648, 24650)
\end{equation*}

[Espiral Pitagórica Par]
Como as medidas dos lados dos triângulos retângulos crescem rapidamente, fica difícil fazer uma espiral como vários triângulos. Portanto, os desenhos acima servem apenas para ilustrar a formação da espiral. Numericamente, podemos observar que a espiral pitagórica par cresce mais rápido que a espiral ímpar.
Este artigo foi cedido gentilmente por Sebastião Vieira do Nascimento (Sebá). Professor Titular (por concurso) aposentado da UFCG – PB, além de colaborador deste blog. Foram feitas algumas alterações do manuscrito original para melhor exposição.
Veja mais
Construindo Raízes de Números Naturais
Construção da Espiral de Arquimedes com Régua e Compasso
Ternos Pitagóricos: A Tábua de Plimpton 322

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a^2}dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a^2}\ dx = \frac{1}{a}\text{arctg}\left(\frac{x}{a}\right) + C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2 + a^2 \neq 0$. Seja a integral:...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral Indefinida Do Produto De Cossenos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation} \int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
