Matemática
Esta é a primeira construção de um pentágono usando régua e compasso. Apesar de tê-la encontrada como sendo um pentágono regular, mostrou-se, por fim, que é apenas uma ótima aproximação, tendo os ângulos internos diferenças menores que $1$ grau.
$2)$ Com centro em $A$, descreva uma circunferência de raio $\overline{AB}$:
$3)$ Com centro em $B$, descreva uma circunferência de raio $\overline{BA}$. Marque os pontos de intersecção entre as duas circunferências como $F$ e $G$:
$4)$ Com centro em $G$, descreva uma terceira circunferência de raio $\overline{GA}$. Marque os pontos de intersecção com as outras duas circunferências como $H$ e $I$:
$5)$ Pelos pontos $F$ e $G$, trace uma reta marcando o ponto $J$ na intersecção com a terceira circunferência. Essa reta será a mediatriz do lado $AB$ do pentágono:
$6)$ Trace uma reta passando pelos pontos $H$ e $J$, definido o ponto $C$ na intersecção com a segunda circunferência. Em seguida, trace uma reta passando pelos pontos $I$ e $J$, definindo o ponto $E$ na intersecção com a primeira circunferência:
$7)$ Com centro em $E$, descreva uma nova circunferência de raio $\overline{EA}$. Em seguida, descreva outra circunferência com centro em $C$ e raio $\overline{CB}$. O ponto de intersecção dessas duas circunferências com a mediatriz define o ponto $D$:
$8)$ Os pontos $A$, $B$, $C$, $D$ e $E$ são os vértices do pentágono:
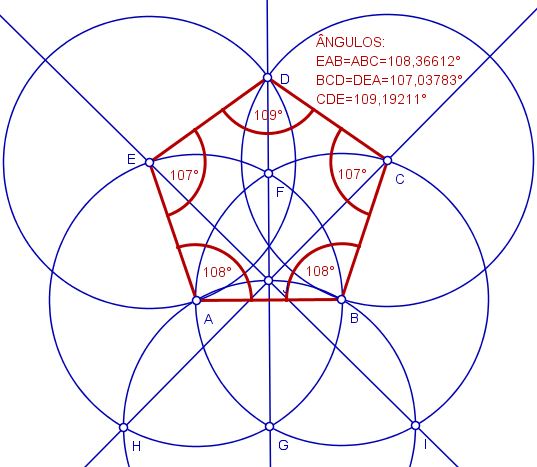
No entanto, o pentágono não é regular. É apenas uma ótima aproximação. A construção foi elaborada pelo software Régua e Compasso. Um recurso deste software é medir ângulos. Vejam a pequena variação nos ângulos internos do pentágono:
Construção de um pentágono com régua e compasso - Parte $3$
Construção de um pentágono com régua e compasso - Parte $4$ - Método de Hirano
- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...
- Construção De Um Decágono Regular Com Régua E Compasso
Esta construção foi elaborada por mim quando estava brincando com o software Régua e Compasso. Provavelmente não seja inédita, mas não encontrei nenhuma fonte que mostre tal construção. Para esta construção, inicie com uma circunferência C1...
- Construção De Um Heptágono Regular Com Régua E Compasso (parte 1)
O Heptágono regular foi fonte de muito mistério na Geometria, quanto à sua construção com régua e compasso, apenas. Gaus provou aos $19$ anos que o heptadecágono regular é construtível com régua e compasso. De seus estudos sobre a contrutibilidade...
- Construção De Um Hexágono Regular Com Régua E Compasso
Neste post, vamos construir um Hexágono regular utilizando régua e compasso. O processo é muito simples. Vamos lá: Comece com um círculo e marque o centro como O: Trace uma reta passando pela origem O e marque as intersecções com a circunferência...
- Construção De Um Pentágono Regular Com Régua E Compasso (parte Ii)
Já vimos no post anterior uma construção de um pentágono regular utilizando régua e compasso. Aqui vou mostrar outro método para construir um pentágono: Comece descrevendo uma circunferência com o compasso com centro em O: Trace, agora, dois...
Matemática
Construção de um pentágono (quase) regular com régua e compasso - Parte $1$
Esta é a primeira construção de um pentágono usando régua e compasso. Apesar de tê-la encontrada como sendo um pentágono regular, mostrou-se, por fim, que é apenas uma ótima aproximação, tendo os ângulos internos diferenças menores que $1$ grau.
Construção:
$1)$ Inicie com um segmento de reta $\overline{AB}$, que será o lado do pentágono:$4)$ Com centro em $G$, descreva uma terceira circunferência de raio $\overline{GA}$. Marque os pontos de intersecção com as outras duas circunferências como $H$ e $I$:
$6)$ Trace uma reta passando pelos pontos $H$ e $J$, definido o ponto $C$ na intersecção com a segunda circunferência. Em seguida, trace uma reta passando pelos pontos $I$ e $J$, definindo o ponto $E$ na intersecção com a primeira circunferência:
No entanto, o pentágono não é regular. É apenas uma ótima aproximação. A construção foi elaborada pelo software Régua e Compasso. Um recurso deste software é medir ângulos. Vejam a pequena variação nos ângulos internos do pentágono:
Veja mais:
Construção de um pentágono com régua e compasso - Parte $2$Construção de um pentágono com régua e compasso - Parte $3$
Construção de um pentágono com régua e compasso - Parte $4$ - Método de Hirano
- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...
- Construção De Um Decágono Regular Com Régua E Compasso
Esta construção foi elaborada por mim quando estava brincando com o software Régua e Compasso. Provavelmente não seja inédita, mas não encontrei nenhuma fonte que mostre tal construção. Para esta construção, inicie com uma circunferência C1...
- Construção De Um Heptágono Regular Com Régua E Compasso (parte 1)
O Heptágono regular foi fonte de muito mistério na Geometria, quanto à sua construção com régua e compasso, apenas. Gaus provou aos $19$ anos que o heptadecágono regular é construtível com régua e compasso. De seus estudos sobre a contrutibilidade...
- Construção De Um Hexágono Regular Com Régua E Compasso
Neste post, vamos construir um Hexágono regular utilizando régua e compasso. O processo é muito simples. Vamos lá: Comece com um círculo e marque o centro como O: Trace uma reta passando pela origem O e marque as intersecções com a circunferência...
- Construção De Um Pentágono Regular Com Régua E Compasso (parte Ii)
Já vimos no post anterior uma construção de um pentágono regular utilizando régua e compasso. Aqui vou mostrar outro método para construir um pentágono: Comece descrevendo uma circunferência com o compasso com centro em O: Trace, agora, dois...