Matemática
![\vec{u}\times \vec{v} =\begin{vmatrix}\vec{i} & \vec{j} & \vec{k}\\ x_1 & y_1 & z_1 \\x_2 & y_2 & z_2 \\ \end{bmatrix} [;\vec{u}\times \vec{v} =\begin{vmatrix}\vec{i} & \vec{j} & \vec{k}\\ x_1 & y_1 & z_1 \\x_2 & y_2 & z_2 \\ \end{bmatrix};]](matematica/matematica-5631d194f1b05.%20=%5Cbegin%7Bvmatrix%7D%5Cvec%7Bi%7D%20&%20%5Cvec%7Bj%7D%20&%20%5Cvec%7Bk%7D%5C%5C%20x_1%20&%20y_1%20&%20z_1%20%5C%5Cx_2%20&%20y_2%20&%20z_2%20%5C%5C%20%5Cend%7Bbmatrix%7D)
![\vec{u}\times \vec{v} = \begin{vmatrix}y_1 & z_1 \\y_2 & z_2 \\ \end{vmatrix}\vec{i} - \begin{vmatrix}x_1 & z_1 \\x_2 & z_2 \\ \end{vmatrix}\vec{j} + \begin{vmatrix}x_1 & y_1 \\x_2 & y_2 \\ \end{vmatrix}\vec{k} [;\vec{u}\times \vec{v} = \begin{vmatrix}y_1 & z_1 \\y_2 & z_2 \\ \end{vmatrix}\vec{i} - \begin{vmatrix}x_1 & z_1 \\x_2 & z_2 \\ \end{vmatrix}\vec{j} + \begin{vmatrix}x_1 & y_1 \\x_2 & y_2 \\ \end{vmatrix}\vec{k};]](matematica/matematica-5631d194f1b05.%20=%20%5Cbegin%7Bvmatrix%7Dy_1%20&%20z_1%20%5C%5Cy_2%20&%20z_2%20%5C%5C%20%5Cend%7Bvmatrix%7D%5Cvec%7Bi%7D%20-%20%5Cbegin%7Bvmatrix%7Dx_1%20&%20z_1%20%5C%5Cx_2%20&%20z_2%20%5C%5C%20%5Cend%7Bvmatrix%7D%5Cvec%7Bj%7D%20+%20%5Cbegin%7Bvmatrix%7Dx_1%20&%20y_1%20%5C%5Cx_2%20&%20y_2%20%5C%5C%20%5Cend%7Bvmatrix%7D%5Cvec%7Bk%7D)
![\vec{u} = (1,-1,2) [;\vec{u} = (1,-1,2);]](matematica/matematica-5631d195714a7.%20=%20%281,-1,2%29) ,
, ![\vec{v}=(2,-1,3) [;\vec{v}=(2,-1,3);]](matematica/matematica-5631d19587191.=%282,-1,3%29) .
.
![\vec{u}\times \vec{v} = \begin{vmatrix}-1 & 2 \\-1 & 3 \\ \end{vmatrix}\vec{i} - \begin{vmatrix}1 & 2 \\2 & 3 \\ \end{vmatrix}\vec{j} + \begin{vmatrix}1 & -1 \\2 & -1 \\ \end{vmatrix}\vec{k} = -\vec{i} + \vec{j} + \vec{k} = (-1,1,1) [;\vec{u}\times \vec{v} = \begin{vmatrix}-1 & 2 \\-1 & 3 \\ \end{vmatrix}\vec{i} - \begin{vmatrix}1 & 2 \\2 & 3 \\ \end{vmatrix}\vec{j} + \begin{vmatrix}1 & -1 \\2 & -1 \\ \end{vmatrix}\vec{k} = -\vec{i} + \vec{j} + \vec{k} = (-1,1,1);]](matematica/matematica-5631d194f1b05.%20=%20%5Cbegin%7Bvmatrix%7D-1%20&%202%20%5C%5C-1%20&%203%20%5C%5C%20%5Cend%7Bvmatrix%7D%5Cvec%7Bi%7D%20-%20%5Cbegin%7Bvmatrix%7D1%20&%202%20%5C%5C2%20&%203%20%5C%5C%20%5Cend%7Bvmatrix%7D%5Cvec%7Bj%7D%20+%20%5Cbegin%7Bvmatrix%7D1%20&%20-1%20%5C%5C2%20&%20-1%20%5C%5C%20%5Cend%7Bvmatrix%7D%5Cvec%7Bk%7D%20=%20-%5Cvec%7Bi%7D%20+%20%5Cvec%7Bj%7D%20+%20%5Cvec%7Bk%7D%20=%20%28-1,1,1%29)
![\mid \vec{u}\times \vec{v}\mid = \sqrt{(-1)^2 + 1^2 + 1^2} = \sqrt{3} [;\mid \vec{u}\times \vec{v}\mid = \sqrt{(-1)^2 + 1^2 + 1^2} = \sqrt{3};]](matematica/matematica-5631d196014b6.)
![\vec{n} = \frac{\vec{u}\times \vec{v}}{\mid \vec{u}\times\vec{v}\mid } = \frac{(-1,1,1)}{\sqrt{3}} [;\vec{n} = \frac{\vec{u}\times \vec{v}}{\mid \vec{u}\times\vec{v}\mid } = \frac{(-1,1,1)}{\sqrt{3}};]](matematica/matematica-5631d195b3310.%20=%20%5Cfrac%7B%5Cvec%7Bu%7D%5Ctimes%20%5Cvec%7Bv%7D%7D%7B%5Cmid%20%5Cvec%7Bu%7D%5Ctimes%5Cvec%7Bv%7D%5Cmid%20%7D%20=%20%5Cfrac%7B%28-1,1,1%29%7D%7B%5Csqrt%7B3%7D%7D)
![1) [;1);]](matematica/matematica-5631d1966e838.) O sinal de
O sinal de ![\det(M) [;\det(M);]](matematica/matematica-5631d1967e17f.) é alterado se permutarmos duas de suas linhas;
é alterado se permutarmos duas de suas linhas;
![2) [;2);]](matematica/matematica-5631d1968cb0c.) Se uma linha de
Se uma linha de ![M [;M;]](matematica/matematica-5631d196508fc.) é multiplicada por
é multiplicada por ![k \in \mathbb{R} [;k \in \mathbb{R};]](matematica/matematica-5631d196b1543.) , então
, então ![\det(kM) = k\det(M) [;\det(kM) = k\det(M);]](matematica/matematica-5631d196c6796.) ;
;
![3) [;3);]](matematica/matematica-5631d1952317e.%29) Se existem duas linhas proporcionais, então
Se existem duas linhas proporcionais, então ![\det(M) = 0 [;\det(M) = 0;]](matematica/matematica-5631d1967e17f.%20=%200) ;
;
![4) [;4);]](matematica/matematica-5631d197062ae.) Se a
Se a ![i [;i;]](matematica/matematica-5631d1971516b.) -ésima linha da matriz
-ésima linha da matriz ![M [;M;]](matematica/matematica-5631d196508fc.) é representada por uma soma, então o determinante pode ser escrito como a soma de dois determinantes em que a
é representada por uma soma, então o determinante pode ser escrito como a soma de dois determinantes em que a ![i [;i;]](matematica/matematica-5631d1971516b.) -ésima linha de cada um deles é formada pelas parcelas da soma.
-ésima linha de cada um deles é formada pelas parcelas da soma.
![\vec{i}\times \vec{j} = \vec{k}, \quad \vec{j}\times \vec{k} = \vec{i} \quad \text{e} \quad \vec{k}\times \vec{i} = \vec{j} [;\vec{i}\times \vec{j} = \vec{k}, \quad \vec{j}\times \vec{k} = \vec{i} \quad \text{e} \quad \vec{k}\times \vec{i} = \vec{j};]](matematica/matematica-5631d197ea308.)
![\vec{i}\times \vec{i} = \vec{j}\times \vec{j} = \vec{k}\times \vec{k} = \vec{0} [;\vec{i}\times \vec{i} = \vec{j}\times \vec{j} = \vec{k}\times \vec{k} = \vec{0};]](matematica/matematica-5631d198050ed.)
![\mid\vec{u}\times \vec{v}\mid^2 + \mid \vec{u}\cdot \vec{v}\mid^2 = \mid\vec{u}\mid^2\ \mid\vec{v}\mid^2 \qquad (1) [;\mid\vec{u}\times \vec{v}\mid^2 + \mid \vec{u}\cdot \vec{v}\mid^2 = \mid\vec{u}\mid^2\ \mid\vec{v}\mid^2 \qquad (1);]](matematica/matematica-5631d19813443.)
![\mid \vec{u}\times \vec{v}\mid^2 = (y_1z_2 - y_2z_1)^2 + (x_1z_2 - x_2z_1)^2 + (x_1y_2 - x_2y_1)^2 [;\mid \vec{u}\times \vec{v}\mid^2 = (y_1z_2 - y_2z_1)^2 + (x_1z_2 - x_2z_1)^2 + (x_1y_2 - x_2y_1)^2;]](matematica/matematica-5631d19837dc6.)
e
![\mid\vec{u}\cdot\vec{v}\mid^2 = (x_1x_2 + y_1y_2 + z_1z_2)^2 [;\mid\vec{u}\cdot\vec{v}\mid^2 = (x_1x_2 + y_1y_2 + z_1z_2)^2;]](matematica/matematica-5631d1984cf7a.)
![\vec{u}\cdot \vec{v} = \mid\vec{u}\mid\ \mid\vec{v}\mid\cos \theta \qquad (2) [;\vec{u}\cdot \vec{v} = \mid\vec{u}\mid\ \mid\vec{v}\mid\cos \theta \qquad (2);]](matematica/matematica-5631d195714a7.%5Ccdot%20%5Cvec%7Bv%7D%20=%20%5Cmid%5Cvec%7Bu%7D%5Cmid%5C%20%5Cmid%5Cvec%7Bv%7D%5Cmid%5Ccos%20%5Ctheta%20%5Cqquad%20%282%29)
Substituindo![(2) [;(2);]](matematica/matematica-5631d198a4edf.) em
em ![(1) [;(1);]](matematica/matematica-5631d1982202e.) , temos:
, temos:
![\mid \vec{u}\times \vec{v}\mid^2 = \mid\vec{u}\mid^2\mid\vec{v}\mid^2 - \mid\vec{u}\mid^2\mid \vec{v}\mid^2\cos^2\theta =\mid\vec{u}\mid^2\mid\vec{v}\mid^2(1 - \cos^2\theta) [;\mid \vec{u}\times \vec{v}\mid^2 = \mid\vec{u}\mid^2\mid\vec{v}\mid^2 - \mid\vec{u}\mid^2\mid \vec{v}\mid^2\cos^2\theta =\mid\vec{u}\mid^2\mid\vec{v}\mid^2(1 - \cos^2\theta);]](matematica/matematica-5631d198cf313.)
![=\mid\vec{u}\mid^2\mid\vec{v}\mid^2(1 - \cos^2\theta) = \mid\vec{u}\mid^2\mid\vec{v}\mid^2\sin \theta [;=\mid\vec{u}\mid^2\mid\vec{v}\mid^2(1 - \cos^2\theta) = \mid\vec{u}\mid^2\mid\vec{v}\mid^2\sin \theta;]](matematica/matematica-5631d198e4d41.)
ou seja,
![\mid\vec{u}\times \vec{v}\mid = \mid\vec{u}\mid\mid\vec{v}\mid\sin \theta [;\mid\vec{u}\times \vec{v}\mid = \mid\vec{u}\mid\mid\vec{v}\mid\sin \theta;]](matematica/matematica-5631d19905e65.)
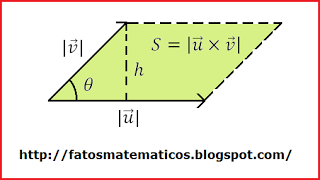
![S = \mid \vec{u}\mid h \qquad (3) [;S = \mid \vec{u}\mid h \qquad (3);]](matematica/matematica-5631d1998eef4.)
![\sin \theta = \frac{h}{\mid\vec{v}\mid} \quad \Rightarrow \quad h =\mid \vec{v}\mid \sin \theta \qquad (4) [;\sin \theta = \frac{h}{\mid\vec{v}\mid} \quad \Rightarrow \quad h =\mid \vec{v}\mid \sin \theta \qquad (4);]](matematica/matematica-5631d1999de74.)
![S = \mid\vec{u}\mid\mid\vec{v}\mid\sin \theta = \mid\vec{u}\times\vec{v}\mid [;S = \mid\vec{u}\mid\mid\vec{v}\mid\sin \theta = \mid\vec{u}\times\vec{v}\mid;]](matematica/matematica-5631d199d1a6b.)
![\vec{u} = \vec{AB} = B - A = (0,1,3) - (-1,2,1) = (1,-1,2) [;\vec{u} = \vec{AB} = B - A = (0,1,3) - (-1,2,1) = (1,-1,2);]](matematica/matematica-5631d195714a7.%20=%20%5Cvec%7BAB%7D%20=%20B%20-%20A%20=%20%280,1,3%29%20-%20%28-1,2,1%29%20=%20%281,-1,2%29)
![\vec{v} = \vec{AC} = C - A = (2,1,-1) - (-1,2,1) = (3,-1,-2) [;\vec{v} = \vec{AC} = C - A = (2,1,-1) - (-1,2,1) = (3,-1,-2);]](matematica/matematica-5631d19587191.%20=%20%5Cvec%7BAC%7D%20=%20C%20-%20A%20=%20%282,1,-1%29%20-%20%28-1,2,1%29%20=%20%283,-1,-2%29)
então,
![\vec{u}\times \vec{v} = (1,-1,2)\times (3,-1,-2) = (4,14,2) [;\vec{u}\times \vec{v} = (1,-1,2)\times (3,-1,-2) = (4,14,2);]](matematica/matematica-5631d194f1b05.%20=%20%281,-1,2%29%5Ctimes%20%283,-1,-2%29%20=%20%284,14,2%29)
onde segue que
![S = \mid \vec{u}\times \vec{v}\mid = \sqrt{4^2 + 14^2 + 2^2} = \sqrt{216} = 6\sqrt{6}\ u.a. [;S = \mid \vec{u}\times \vec{v}\mid = \sqrt{4^2 + 14^2 + 2^2} = \sqrt{216} = 6\sqrt{6}\ u.a.;]](matematica/matematica-5631d19a9cd19.)
- Sobre O Produto Misto
Prof. Paulo Sérgio, Blog Fatos Matemáticos. O Produto Misto tem seu destaque na Álgebra Vetorial devido a sua interpretação geométrica que está relacionado ao volume de paralelepípedo ou tetraedro...
- Sobre O Produto Escalar
Por: Prof. Paulo Sérgio, Blog Fatos Matemáticos O Produto Escalar dos vetores e , denotado por é definido por: Segue desta definição que . Além disso, se é o ângulo entre dois vetores e...
- Vetores
Fonte: Site Baricentro da Mente. (http://obaricentrodamente.blogspot.com) Em Física, algumas grandezas necessitam definir o sentido e a direção. Estas grandezas são chamadas de Vetores, dentre elas o deslocamento, velocidade,...
- Uma Demonstração Da Desigualdade De Schwarz (em Espaços Reais)
Hermann Amandus Schwarz (1843-1921) O objetivo desta postagem é apresentar uma demonstração da desigualdade de Schwarz (não confundir com Schwartz), que enuncia o seguinte: Se $$u$$ e $$v$$ são elementos de um espaço vetorial real com produto...
- Vetores Exercícios
Esse é o blog de Antonio Carneiro, Professor e Articulador do gestar de Matemática do Estado da Bahia no Colégio Est. Dinah Gonçalves em Valéria, Salvador-bahia e Biologia na rede privada. graduado Em Ciências Naturais UFBA e pós graduado em Metodologia...
Matemática
Sobre o Produto Vetorial

Mais um ótimo post do Blog Fatos Matemáticos do Profº Paulo Sergio
O produto vetorial é uma ferramenta muito importante na Física e na Matemática Aplicada, pois através dela podemos calcular a área de um triângulo ou paralelogramo definido por dois vetores. O torque pode também ser definido através do produto vetorial.
Definição 1: O produto vetorial dos vetores ![\vec{u} = (x_1,y_1,z_1) = x_1\vec{i} + y_1\vec{j} + z_1\vec{k} [;\vec{u} = (x_1,y_1,z_1) = x_1\vec{i} + y_1\vec{j} + z_1\vec{k};]](matematica/matematica-5631d194ce34d.) e
e ![\vec{v} = (x_2,y_2,z_2) = x_2\vec{i} + y_2\vec{j} + z_2\vec{k} [;\vec{v} = (x_2,y_2,z_2) = x_2\vec{i} + y_2\vec{j} + z_2\vec{k};]](matematica/matematica-5631d194dcc5f.) , tomados nesta ordem e denotado por
, tomados nesta ordem e denotado por ![\vec{u}\times \vec{v} [;\vec{u}\times \vec{v};]](matematica/matematica-5631d194f1b05.) é definido por
é definido por
Desta expressão vemos que o produto vetorial de dois vetores é um vetor. Para resolver o determinante podemos usar o método de Sarrus em que repete a primeira e a segunda coluna. Particularmente, eu prefiro usar o método de Laplace que consiste em transformar o determinante acima em ![3 [;3;]](matematica/matematica-5631d1952317e.) determinantes
determinantes ![2\times 2 [;2\times 2;]](matematica/matematica-5631d195383ec.) , isto é,
, isto é,
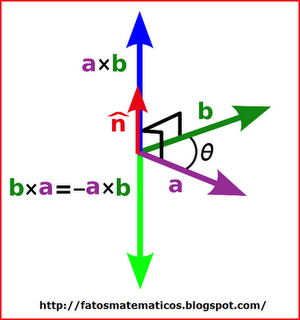
Usando essa expressão, segue que ![(\vec{u}\times\vec{v})\cdot \vec{u} = (\vec{u}\times\vec{v})\cdot \vec{v} = 0 [;(\vec{u}\times\vec{v})\cdot \vec{u} = (\vec{u}\times\vec{v})\cdot \vec{v} = 0;]](matematica/matematica-5631d1955c25f.) , ou seja, o produto vetorial é um vetor mutuamente ortogonal aos vetores
, ou seja, o produto vetorial é um vetor mutuamente ortogonal aos vetores ![\vec{u} [;\vec{u};]](matematica/matematica-5631d195714a7.) e
e ![\vec{v} [;\vec{v};]](matematica/matematica-5631d19587191.) .
.
Exemplo 1: Determine um vetor unitário e ortogonal ao plano definido pelos vetores
Resolução: Seja ![\vec{n} [;\vec{n};]](matematica/matematica-5631d195b3310.) o vetor pedido. Usando o desenvolvimento de Laplace, temos:
o vetor pedido. Usando o desenvolvimento de Laplace, temos:
Pelo comentário acima, este vetor é ortogonal ao plano definido pelos vetores  e
e ![\vec{v} [;\vec{v};]](matematica/matematica-5631d19587191.) , mas
, mas
Para obter o vetor unitário ![\vec{n} [;\vec{n};]](matematica/matematica-5631d195b3310.) , basta dividir
, basta dividir  pelo seu módulo, isto é,
pelo seu módulo, isto é,
As propriedades do produto vetorial decorrem diretamente das propriedades dos determinantes. Assim, se ![M [;M;]](matematica/matematica-5631d196508fc.) uma matriz
uma matriz ![n\times n [;n\times n;]](matematica/matematica-5631d19660271.) de números reais, então:
de números reais, então:
Da propriedade ![1) [;1);]](matematica/matematica-5631d1966e838.) , segue que
, segue que ![\vec{v}\times \vec{u} = - \vec{u}\times \vec{v} [;\vec{v}\times \vec{u} = - \vec{u}\times \vec{v};]](matematica/matematica-5631d19587191.%5Ctimes%20%5Cvec%7Bu%7D%20=%20-%20%5Cvec%7Bu%7D%5Ctimes%20%5Cvec%7Bv%7D) ;
;
Da propriedade ![2) [;2);]](matematica/matematica-5631d1968cb0c.) , obtemos
, obtemos ![(k\vec{u})\times \vec{v} = k(\vec{u}\times \vec{v}) [;(k\vec{u})\times \vec{v} = k(\vec{u}\times \vec{v});]](matematica/matematica-5631d1977c5ec.) ;
;
A propriedade ![(k\vec{u})\times \vec{u} = \vec{0} [;(k\vec{u})\times \vec{u} = \vec{0};]](matematica/matematica-5631d1978b1e6.) , segue da propriedade
, segue da propriedade ![3) [;3);]](matematica/matematica-5631d1952317e.%29) ;
;
E a propriedade ![\vec{u}\times (\vec{v} + \vec{w}) = \vec{u}\times \vec{v} + \vec{u}\times \vec{w} [;\vec{u}\times (\vec{v} + \vec{w}) = \vec{u}\times \vec{v} + \vec{u}\times \vec{w};]](matematica/matematica-5631d195714a7.%5Ctimes%20%28%5Cvec%7Bv%7D%20+%20%5Cvec%7Bw%7D%29%20=%20%5Cvec%7Bu%7D%5Ctimes%20%5Cvec%7Bv%7D%20+%20%5Cvec%7Bu%7D%5Ctimes%20%5Cvec%7Bw%7D) é consequência da propriedade
é consequência da propriedade ![4) [;4);]](matematica/matematica-5631d197062ae.) .
.
Da primeira propriedade, vemos que existem apenas dois vetores unitários ortogonais ao plano formado pelos vetores ![\vec{u} [;\vec{u};]](matematica/matematica-5631d195714a7.) e
e ![\vec{v} [;\vec{v};]](matematica/matematica-5631d19587191.) . É interessante notar que
. É interessante notar que
e que
Para ver a interpretação geométrica do produto vetorial, usaremos a identidade de Lagrange, dada por
A demonstração de ![(1) [;(1);]](matematica/matematica-5631d1982202e.) é clássica e basta desenvolver o membro esquerdo usando as expressões:
é clássica e basta desenvolver o membro esquerdo usando as expressões:
e
Deixo para o leitor verificar a expressão ![(1) [;(1);]](matematica/matematica-5631d1982202e.) . Por outro lado, o produto escalar de
. Por outro lado, o produto escalar de ![\vec{u} [;\vec{u};]](matematica/matematica-5631d195714a7.) e
e ![\vec{v} [;\vec{v};]](matematica/matematica-5631d19587191.) é dado por
é dado por
Substituindo
ou seja,
Proposição 1: Geometricamente o módulo do produto vetorial de dois vetores representa a área do paralelogramo formado por esses vetores.

De fato, da figura acima, a área do paralelogramo é
Mas,
Substituindo ![(4) [;(4);]](matematica/matematica-5631d199accd3.) em
em ![(3) [;(3);]](matematica/matematica-5631d199c2aa1.) , temos:
, temos:
Observação: Segue deste resultado que a área do triângulo definido pelos vetores ![\vec{u} [;\vec{u};]](matematica/matematica-5631d195714a7.) e
e ![\vec{v} [;\vec{v};]](matematica/matematica-5631d19587191.) é a metade do módulo do produto vetorial.
é a metade do módulo do produto vetorial.
Exemplo 2: Determine a área do paralelogramo determinado pelos vetores ![\vec{u} = \vec{AB} [;\vec{u} = \vec{AB};]](matematica/matematica-5631d195714a7.%20=%20%5Cvec%7BAB%7D) e
e ![\vec{v} = \vec{AC} [;\vec{v} = \vec{AC};]](matematica/matematica-5631d19587191.%20=%20%5Cvec%7BAC%7D) , sendo
, sendo ![A(-1,2,1) [;A(-1,2,1);]](matematica/matematica-5631d19a36dee.) ,
, ![B(0,1,3) [;B(0,1,3);]](matematica/matematica-5631d19a45a1b.) e
e ![C(2,1,-1) [;C(2,1,-1);]](matematica/matematica-5631d19a54126.) .
.
Resolução: Sendo
e
então,
onde segue que
- Sobre O Produto Misto
Prof. Paulo Sérgio, Blog Fatos Matemáticos. O Produto Misto tem seu destaque na Álgebra Vetorial devido a sua interpretação geométrica que está relacionado ao volume de paralelepípedo ou tetraedro...
- Sobre O Produto Escalar
Por: Prof. Paulo Sérgio, Blog Fatos Matemáticos O Produto Escalar dos vetores e , denotado por é definido por: Segue desta definição que . Além disso, se é o ângulo entre dois vetores e...
- Vetores
Fonte: Site Baricentro da Mente. (http://obaricentrodamente.blogspot.com) Em Física, algumas grandezas necessitam definir o sentido e a direção. Estas grandezas são chamadas de Vetores, dentre elas o deslocamento, velocidade,...
- Uma Demonstração Da Desigualdade De Schwarz (em Espaços Reais)
Hermann Amandus Schwarz (1843-1921) O objetivo desta postagem é apresentar uma demonstração da desigualdade de Schwarz (não confundir com Schwartz), que enuncia o seguinte: Se $$u$$ e $$v$$ são elementos de um espaço vetorial real com produto...
- Vetores Exercícios
Esse é o blog de Antonio Carneiro, Professor e Articulador do gestar de Matemática do Estado da Bahia no Colégio Est. Dinah Gonçalves em Valéria, Salvador-bahia e Biologia na rede privada. graduado Em Ciências Naturais UFBA e pós graduado em Metodologia...
