Matemática

- Questão 41 ? Processo De Promoção ? Quadro Do Magistério ? Professor De Educação Básica Ii ? Matemática ? São Paulo
Carl Boyer, em seu livro História da Matemática, apresenta e discute ideias de Euclides de Alexandria, que é o autor de Os Elementos. Para Boyer, os Elementos ?não só constituem a mais antiga obra matemática grega importante a chegar até nós,...
- Tentativas De Demonstração Do Quinto Postulado De Euclides Do Século Iii A.c. Ao Século Xxi.
Aproximadamente em 300 a. C., Euclides escreveu os Elementos. No século I a.C., Posidônio apresentou uma definição de paralelismo segundo a qual as retas paralelas...
- A Demonstração Do Quinto Postulado De Euclides Por Proclus
Proclus Diadochus nasceu em Constantinopla por volta do ano 410. Terá ido aprender filosofia para Alexandria e,...
- A Demonstração Do Quinto Postulado De Euclides Por Ptolomeu
Ptolomeu, ou Claudius Ptolemaeus, foi geógrafo e astrônomo e viveu no século II, em Alexandria. Foi o autor de um famoso tratado de astronomia em 13 livros, que chegou até à...
- A Demonstração Do Quinto Postulado De Euclides - Postulado Das Paralelas
Sabe-se muito pouco sobre Euclides. Sabe-se que nasceu depois dos discípulos diretos de Platão, mas antes de Erastóstenes e Arquimedes e que viveu em Alexandria...
Matemática
A Demonstração do Quinto Postulado de Euclides por Aganis

Outra tentativa de demonstrar o quinto postulado aparece no comentário árabe de Al-Nirizi(século IX) que chegou aos nossos dias através de uma tradução para latim de Gerardo de Cremona (século XII). Esta tentativa é atribuída a um tal de Aganis.
Não se sabe ao certo quem foi Aganis, há quem o identifique com Geminus, mas também há quem negue essa possibilidade. Simpliciusviveu no século VI, como Aganis foi seu amigo ou mestre, pressupõe-se que tenha vivido por essa altura.
Al-Nirizi, na parte do seu comentário dedicada às definições, postulados e axiomas, inclui muitas referências a Simplicius (século VI). Ao que parece, Simplicius terá escrito um comentário ao primeiro livro dos Elementos de Euclides em que declarava ser possível demonstrar o quinto postulado. O comentarista árabe aceitou sem questionar as idéias e demonstrações do sue antecessor e cita Simplicius que, por sua vez, apresenta a demonstração do seu amigo (ou mestre) Aganis para o quinto postulado.
Simpliciusdiz que este postulado requer demonstração e que Abthinathus e Diodorus já o tinham demonstrado recorrendo a muitas proposições diferentes, enquanto que Ptolomeu o havia explicado e demonstrado usando proposições dos Elementos de Euclides.
Sobre quem seja Abthinathus apenas há especulações. Já no que toca a Diodorus, acredita-se que seja o autor do Analemma, sobre o qual Pappusescreveu um comentário. Esta referência mostra que nesta altura já eram vários os que haviam contestado o quinto postulado de Euclides (e vários os que julgavam ter conseguido demonstrá-lo, se bem que estivessem enganados pois é impossível demonstrar o quinto postulado sem recorrer a um novo postulado). Ficamos também a saber que Simpliciusnão se apercebeu do erro da demonstração de Ptolomeu.
No seu comentário, Simplicius apresenta idéias similares às de Posidônio. Por isso, não causa grande surpresa que Aganis (citado por Simplicius) cometa o erro de, como Posidônio, chamar paralelas a linhas retas eqüidistantes. Ou seja, está a pressupor que, se duas retas não se intersectam, então, elas mantêm-se sempre à mesma distância e, como já referi, isso implica o quinto postulado, pelo que a demonstração não faz sentido.
No referido comentário, é citada a definição de paralelismo do filósofo Aganis:
?Linhas retas paralelas são linhas retas, situadas no mesmo plano, cujas distâncias entre si, se prolongadas indefinidamente em ambas as direções ao mesmo tempo, é sempre a mesma? (Heath, 1925, p. 191).
Para clarificar esta definição, Simplicius diz que;
?A distância referida é a linha mais curta que liga coisas desligadas e no que se refere à distância entre duas linhas, essa distância é, se as linhas forem paralelas, uma e a mesma, igual a si própria em todos os pontos da reta, é a distância mais curta e, em todos os pontos da reta, é perpendicular a ambas? (Heath, 1925, p. 191).
A partir da sua definição de paralelismo, Aganis constrói uma demonstração do quinto postulado deduzindo as seguintes proposições: a distância mais curta entre duas paralelas é a perpendicular comum a ambas as linhas; duas linhas retas perpendiculares a uma terceira são paralelas entre si; duas paralelas, cortadas por uma terceira linha reta, formam ângulos internos no mesmo lado que são suplementares (iguais a dois ângulos retos) e reciprocamente.
Esta última proposição é similar à proposição 29 do primeiro livro dos Elementos de Euclides, proposição essa que carece do quinto postulado para ser corretamente demonstrada. Mas, ao pressupor aquela definição de paralelismo, já se pressupõe o quinto postulado e, portanto, podem-se demonstrar as três proposições referidas.
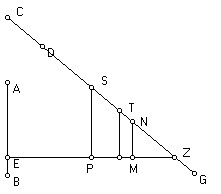
Eis como Aganis constrói o ponto de intersecção de duas linhas retas que não são eqüidistantes (de acordo com Bonola, 1912, p.8-9):
- Sejam AB e GD duas linhas retas cortadas por uma transversal EZ, de modo que a soma dos ângulos AEZ e EZD seja menor que dois ângulos retos;
- Suponha-se, sem perda de generalidade, que AEZ é um ângulo reto;
- Tome-se um ponto arbitrário T sobre ZD;
- A partir de T trace-se TL perpendicular a ZE;
- Bissecte-se o segmento EZ em P; bissecte-se PZ em M; bissecte-se MZ, etc.. até um dos pontos médios P, M, ... estar no segmento LZ. Seja esse o ponto M;
- Trace-se MN perpendicular a EZ, a encontrar ZD em N;
- Sobre ZD, marque-se o segmento ZC, o mesmo múltiplo de ZN que ZE é de ZM;
- No caso da figura, ZC = 4 ZN.
- O ponto C assim encontrado é o ponto de intersecção das duas linhas retas AB e GD.

Para provar isto, seria necessário mostrar que os segmentos ZN, NS,... que foram marcados um após o outro sobre a linha ZD, têm iguais projeções sobre ZE. O raciocínio apresenta algumas semelhanças com uma parte da demonstração de Nasiraddindo quinto postulado.
REFERÊNCIAS
Autor do Artigo: MARQUES, Hugo. "As tentativas de demonstração do Quinto Postulado dos Elementosde Euclides". Faculdade de Ciências da Universidade de Lisboa. 2004
BONOLA, Roberto, Non-Euclidean Geometry, tradução inglesa de H. S. Carslaw; New York: Dover Publications Inc, 1955.
LOBACHEVSKY, Nicholas, The Theory of Parallels, tradução inglesa de George Bruce Halsted, in BONOLA, Roberto, Non-Euclidean Geometry, tradução inglesa de H. S. Carslaw; New York: Dover Publications Inc, 1955.
BOLYAI, John, The Science of Absolute Space, tradução inglesa de George Bruce Halsted, in BONOLA, Roberto, Non-Euclidean Geometry, tradução inglesa de H. S. Carslaw; New York: Dover Publications Inc, 1955.
DUDLEY, Underwood, Mathematical Cranks, Washington D.C.: The Mathematical Association of America, 1992 .
HEAT, Thomas, L., The thirteen books of Euclid?s Elements translated with introduction and commentary (volume 1), New York: Dover Publications Inc, 1956 (edição original 1925).
GREENBERG, Marvin Jay, Euclidean and Non-Euclidean Geometries: Development and History, San Francisco: W. H. Freeman and Company, 1980.
PROCLUS, A Commentary on the first book os Euclid?s Elements, tradução inglesa de Glenn R. Morrow, New Jersey: Princeton University Press, 1970.
VELOSO, Eduardo, Geometria, Temas Actuais: Materiais para Professores, Lisboa: IIE, 1998.
- Questão 41 ? Processo De Promoção ? Quadro Do Magistério ? Professor De Educação Básica Ii ? Matemática ? São Paulo
Carl Boyer, em seu livro História da Matemática, apresenta e discute ideias de Euclides de Alexandria, que é o autor de Os Elementos. Para Boyer, os Elementos ?não só constituem a mais antiga obra matemática grega importante a chegar até nós,...
- Tentativas De Demonstração Do Quinto Postulado De Euclides Do Século Iii A.c. Ao Século Xxi.
Aproximadamente em 300 a. C., Euclides escreveu os Elementos. No século I a.C., Posidônio apresentou uma definição de paralelismo segundo a qual as retas paralelas...
- A Demonstração Do Quinto Postulado De Euclides Por Proclus
Proclus Diadochus nasceu em Constantinopla por volta do ano 410. Terá ido aprender filosofia para Alexandria e,...
- A Demonstração Do Quinto Postulado De Euclides Por Ptolomeu
Ptolomeu, ou Claudius Ptolemaeus, foi geógrafo e astrônomo e viveu no século II, em Alexandria. Foi o autor de um famoso tratado de astronomia em 13 livros, que chegou até à...
- A Demonstração Do Quinto Postulado De Euclides - Postulado Das Paralelas
Sabe-se muito pouco sobre Euclides. Sabe-se que nasceu depois dos discípulos diretos de Platão, mas antes de Erastóstenes e Arquimedes e que viveu em Alexandria...
