Matemática

Análise combinatória- Parte I

Olá gente! Hoje falarei sobre análise combinatória. Nesse primeiro post sobre o assunto pretendo apenas introduzir alguns conceitos básicos.

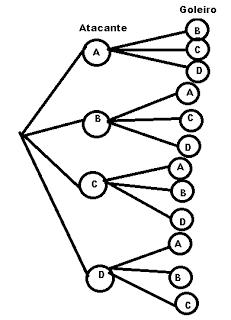
Q-1) Dentre 4 jogadores de futebol, de quantas formas podemos escolher 1 atacante e 1 goleiro.

Esse problema ilustra o principio multiplicativo, que é enunciado da seguinte forma:

Se há K formas de tomar uma decisão A e não importando a decisão tomada há L formas de tomar a decisão B, então podemos tomar consecutivamente as decisões A e B de $[;K \cdot L;]$ formas.

De fato:

Para escolher o atacante temos 4 opções, para cada atacante que for escolhido há 3 formas de escolher o goleiro.

Assim, o número total de formas de escolher essa dupla é $[;4 \cdot 3= 12;]$ .

Se restar dúvida, observe a arvore de possibilidades abaixo, ela lista todos os casos.

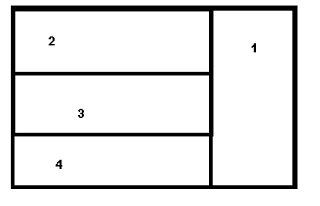
Q-2) De quantas formas podemos colorir a figura abaixo se dispormos de 4 cores e partes que possuam um segmento em comum não podem ter a mesma cor?

Observe que escolher a ordem em que iremos pintar a bandeira é essencial, caso contrário teremos grandes problemas mais tarde. Quando isso ocorrer, comece sempre pelo caso mais restrito, que no problema é a região 1.

Para pintar a parte 1 temos 4 possibilidades, depois de pintar a parte 1 há 3 formas de pintar a parte 2, a parte 3 pode ser pintada de 2 formas, pois não pode ter a mesma cor que as partes 1 e 2, e a parte quatro pode ser pintada também de 2 formas, pois não pode ter a mesma cor que as partes 1 e 3. Pelo princípio multiplicativo, há $[;4 \cdot 3 \cdot 2 \cdot 2 = 48;]$

formas de pintar essa figura.

Q-3) De quantas formas podemos colocar 11 pessoas em fila?

Há 11 formas de escolher quem ocupará o primeiro lugar, 10 para o segundo, 9 para o terceiro... 2 para o décimo e 1 para o décimo primeiro. Logo, há $[;11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 39916800;]$ modos de formar essa fila.

De modo geral, para ordenar n objetos distintos há $[;n \cdot (n-1) \cdots 2 \cdot 1;]$ formas de fazê-lo. Lê-se n fatorial e representamos como "n!".

Q-4) De quantas formas 5 pessoas podem se sentar formando uma roda?

A primeira pessoa pode ser escolhida de 5 formas, a segunda de 4 formas, a terceira de 3, a segunda de 2 e a ultima só de 1 forma. Porém as rodas ABCDE, BCDEA, CDEAB, DEABC e EABCD são equivalentes, logo são $[;\frac{5!}{5}=4!;]$ maneiras de formar essa roda.

Generalizando um pouco, o número de maneiras de dispor n objetos em um circulo, se as rotações coincidirem é o número de maneiras que as pessoas podem ser permutadas, dividido pelo número de rotações, que é: $[;\frac{n!}{n}=(n-1)!;]$

Esse tipo de combinação é chamado de permutação circular.

Q-5) Dentre uma turma de 20 pessoas, queremos selecionar 3 para serem representantes de turma. De quantas maneiras podemos escolher esses representantes?

Sendo A um conjunto de n elementos, definimos $[;{n \choose k};]$ (lê-se n escolhe k) como o número de subconjuntos de A que possuem k elementos. Sendo $[;{n \choose k}= \frac{n!}{k!(n-k)!};]$ . De fato, o primeiro elemento pode ser escolhido de n formas, o segundo de (n-1)... o k-ésimo elemento pode ser escolhido de (n-k+1). Porém esses k elementos podem ser permutados entre si de [;k!;]

formas, assim, o número de maneiras de escolher os k elementos é

$[;\frac{n\cdot(n-1)\cdots (k+1) \cdot k}{k!} = \frac{n!}{k! (n-k)!};]$ .

Logo, há $[;\frac{20!}{3! \cdot 17!}= 1140;]$ maneiras de escolher esses representantes.

ALGUMAS PROPRIEDADES!

Se n e k são números inteiros positivos com [;n>k;]

, então:

P.1- $[;{n \choose k}={n \choose (n-k)};]$

De fato, por definição $[;{n \choose k} = \frac{n!}{k! (n-k)!};]$ e

$[;{n \choose (n-k)} = \frac{n!}{(n-k)![n-(n-k)]!}= \frac{n!}{(n-k)!k!};]$

P.2-

$[;{n \choose k} = \frac{n}{k} {(n-1) \choose (k-1)};]$ (fórmula da absorção)

Para demonstrar é só aplicar a definição!

P.3- $[;{n \choose k} = {(n-1) \choose k} + {(n-1) \choose (k-1)};]$ (relação de Stifel)

$[;{(n-1) \choose k} + {(n-1) \choose (k-1)} = \frac{(n-1)!}{k! \cdot (n-k-1)!} + \frac{(n-1)!}{(k-1)! \cdot (n-k)!} =;]$

$[;= \frac{(n-1)! \cdot (n-k) + (n-1)! \cdot k}{k! \cdot (n-k)!}=;]$ $[; \frac{(n-1) \cdot (n-k+k)}{k! \cdot (n-k)!}=;]$

$[;=\frac{n!}{k! \cdot (n-k)!};]$ $[;= {n \choose k};]$

C.Q.D.

P.4- $[;{k \choose k} + {(k+1) \choose k} + \cdots + {n \choose k} = {(n+1) \choose (k+1)};]$

Vamos usar indução em n.

$[;{k \choose k} = {(k+1) \choose (k+1)} = 1;]$

Se $[;{k \choose k} + {(k+1) \choose k} + \cdots + {n \choose k} = {(n+1) \choose (k+1)};]$

então $[;{k \choose k} + {(k+1) \choose k} + \cdots + {n \choose k} + {(n+1) \choose k} =;]$ $[;{(n+1) \choose (k+1)};]$ $[; + {(n+1) \choose k};]$

Pela propriedade 3...

$[;{(n+1) \choose (k+1)} + {(n+1) \choose k} = {(n+2) \choose (k+1)};]$

C.Q.D.

P.5- $[;{n \choose 0} + {n \choose 1} + \cdots + {n \choose n} = 2^n;]$

Para demonstrar essa propriedade vamos pensar no que essa soma representa.

Se $[;{n \choose k};]$ é o número de subconjuntos com k elementos de um conjunto com n elementos, então essa soma mostra quantos subconjuntos um conjunto de n elementos tem no total.

Logo, precisamos contar de quantas maneiras podemos formar esse subconjunto. Cada um dos n elementos tem 2 opções, estar ou não nesse subconjunto que queremos formar. Logo, pelo principio multiplicativo, são [;2^n;]

maneiras de formar esse subconjunto.

Por hoje é só! Espero que este post tenha sido util. Brevemente voltarei com algumas coisas um pouco mais avançadas sobre combinatória. Se você gostou, recomende aos seus amigos nas redes sociais e se inscreva por e-mail para receber nossas atualizações.

Lembre-se: Para melhorar a qualidade de nossas postagens avalie este post nas caixas logo abaixo. É rapidinho!

Até mais!
Fonte:

Apostila 2 distribuina no Programa de Iniciação Científica da OBMEP - Você pode baixa-la clicando aqui

Apostila da aula 3 do curso de combinatória do POTI (Polo de Treinamento Intensivo) escrita pelo Prof. Carlos Shine - Você pode vizualiza-la clicando aqui

- Os Lemas De Kaplansky
Olá pessoal, hoje estamos escrevendo sobre os lemas de Kaplansky. Suponha que você se depare com o seguinte problema: 1- De quantas formas pode-se escolher subconjuntos de 3 elementos do conjunto {1,2,3,4,5,6,7} sendo que não pode haver números consecutivos?...

- Combinatória
Combinatória é a parte da matemática que se preocupa em agrupar e contar coleções de objetos, seguindo certos critérios de contagem. Tais contagens podem ser feitas de duas maneiras: princípio aditivo e princípio multiplicativo.Princípio...

- Combinações
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com Quando...

- Combinações
Professor de Matemática Antonio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] HTTP://ensinodematemtica.blogspot.comhttp://accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.comQuando formamos...

- Combinações
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...

Matemática