Matemática
MEDIDA DE UM ÂNGULO
A medida de um ângulo é dada pela medida de sua abertura. A unidade padrão de medida de um ângulo é o grau, cujo símbolo é º.
Tomando um ângulo raso ou de meia-volta e dividindo-o em 180 partes iguais, determinamos 180 ângulos de mesma medida. Cada um desses ângulos representa um ângulo de 1º grau (1º).
Para medir ângulos utilizamos um instrumento denominado transferidor. O transferidor já vem graduado com divisões de 1º em 1º. Existem dois tipos de transferidor: Transferidor de 180º e de 360º.
O grau compreende os submúltiplos:
Logo, podemos concluir que:
Quando um ângulo é medido em graus, minutos e segundos, estamos utilizando o sistema sexagesimal.
Como medir um ângulo, utilizando o transferidor
Observe a seqüência
Observe as seguintes indicações de ângulos e suas respectivas leituras:
15º (lê-se "15 graus'')
45º50' (lê-se ''45 graus e 50 minutos'')
30º48'36'' (lê-se ''30 graus, 48 minutos e 36 segundos'')
Observações
Além do transferidor, existem outros instrumentos que medem ângulos com maior precisão. Como exemplos temos o teodolito, utilizado na agrimensura, e o sextante, utilizado em navegação.
A representação da medida de um ângulo pode também ser feita através de uma letra minúscula ou de um número.
Um ângulo raso ou de meia-volta mede 180º.
O ângulo de uma volta mede 360º.
Questões envolvendo medidas de ângulos
Observe a resolução das questões abaixo:
Solução
Medida de AÔB = x
Medida de BÔC = 105º
Como m ( AÔC) é 180º, pois é um ângulo raso, temos:
m (AÔB) + m (BÔC) = m (AÔC)
x + 105º = 180º
x = 180º - 105º
x = 75º
Logo, a medida de AÔB é 75º.
Solução
Verificamos que o ângulo não-convexo na figura (x) e o ângulo convexo (50º) formam, juntos, um ângulo de uma volta, que mede 360º. Assim:
Medidas fracionárias de um ângulo
Subtração
Observe os exemplos:
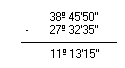
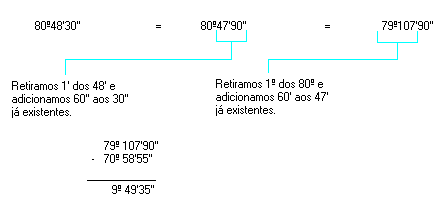
Logo, a diferença é 9º 49'35''.
Multiplicação por um número natural
Observe os exemplos:
Divisão por um número natural
Observe os exemplos:
- Geometria
Estudando Ãngulos Estudando os ângulos Ângulo é a abertura formada entre duas semirretas de mesma origem. Observe:A unidade de representação do ângulo é o grau (º). Classificamos um ângulo em agudo, reto ou obtuso. Ângulo reto:...
- Ângulos
Denominamos ângulo a região do plano limitada por duas semirretas de mesma origem. As semirretas recebem o nome de lados do ângulo e a origem delas, de vértice do ângulo. A unidade usual de medida de ângulo, de acordo com o sistema de medidas,...
- Ângulos
Ângulo é a reunião de duas semi-retas de mesma origem e não-colineares. Na figura Indicação do ângulo: AÔB, ou BÔA ou simplismente Ô PONTOS INTERNOS E PONTOS EXTERNOS A UM ÂNGULO Seja o ângulo AÔB MEDIDA DE UM ÂNGULO Um ângulo...
- Ângulos
Ângulo é a reunião de duas semi-retas de mesma origem e não-colineares. Na figura Indicação do ângulo: AÔB, ou BÔA ou simplismente Ô PONTOS INTERNOS E PONTOS EXTERNOS A UM ÂNGULO Seja o ângulo AÔB MEDIDA DE UM ÂNGULO Um...
- Ângulos
Ângulo é a reunião de duas semi-retas de mesma origem e não-colineares. Na figura Indicação do ângulo: AÔB, ou BÔA ou simplismente Ô PONTOS INTERNOS E PONTOS EXTERNOS A UM ÂNGULO Seja o ângulo AÔB MEDIDA DE UM ÂNGULO Um...
Matemática
Ângulos
Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email [email protected]
www.ensinodematemtica.blogspot.com.br
www.accbarrosogestar.blogspot.com.br
WWW.profantoniocarneiro.com
fonte:http://www.somatematica.com.br
Observe agora dois casos em que as semi-retas de mesma origem estão contidas na mesma reta. Nesses casos, formam-se também ângulos.- As semi-retas
coincidem. Temos aí o ângulo nulo e o ângulo de uma volta.
- As semi-retas
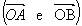não coincidem. Temos aí dois ângulos rasos ou de meia-volta.
Podemos, então, estabelecer que:
| Ângulo é a região do plano limitada por duas semi-retas que têm a mesma origem. |
A medida de um ângulo é dada pela medida de sua abertura. A unidade padrão de medida de um ângulo é o grau, cujo símbolo é º.
Tomando um ângulo raso ou de meia-volta e dividindo-o em 180 partes iguais, determinamos 180 ângulos de mesma medida. Cada um desses ângulos representa um ângulo de 1º grau (1º).
O grau compreende os submúltiplos:
- O minuto corresponde a
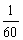do grau. Indica-se um minuto por 1'.
| 1º=60' |
- O segundo corresponde a 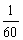do minuto. Indica-se um segundo por 1''.
| 1'=60'' |
1º = 60'.60 = 3.600'' |
Como medir um ângulo, utilizando o transferidor
Observe a seqüência
- O centro O do transferidor deve ser colocado sobre o vértice do ângulo.
- A linha horizontal que passa pelo centro deve coincidir com uma das semi-retas do ângulo
. - Verificamos a medida da escala em que passa a outra semi-reta
.
Observe as seguintes indicações de ângulos e suas respectivas leituras:
15º (lê-se "15 graus'')
45º50' (lê-se ''45 graus e 50 minutos'')
30º48'36'' (lê-se ''30 graus, 48 minutos e 36 segundos'')
Observações
Além do transferidor, existem outros instrumentos que medem ângulos com maior precisão. Como exemplos temos o teodolito, utilizado na agrimensura, e o sextante, utilizado em navegação.
A representação da medida de um ângulo pode também ser feita através de uma letra minúscula ou de um número.
Um ângulo raso ou de meia-volta mede 180º.
O ângulo de uma volta mede 360º.
Questões envolvendo medidas de ângulos
Observe a resolução das questões abaixo:
- Determine a medida do ângulo AÔB na figura:
Medida de AÔB = x
Medida de BÔC = 105º
Como m ( AÔC) é 180º, pois é um ângulo raso, temos:
m (AÔB) + m (BÔC) = m (AÔC)
x + 105º = 180º
x = 180º - 105º
x = 75º
Logo, a medida de AÔB é 75º.
- Determine a medida do 6angulo não-convexo na figura:
Verificamos que o ângulo não-convexo na figura (x) e o ângulo convexo (50º) formam, juntos, um ângulo de uma volta, que mede 360º. Assim:
x + 50º = 360º
x = 360º - 50º
x = 310º
Logo, o valor do ângulo não-convexo é 310º. Como construir um ângulo utilizando o transferidor
Observe a seqüência utilizada na construção de um ângulo de 50º:
- Traçamos uma semi-reta
.
- Colocamos o centro do transferidor sobre a origem da semi-reta (A).
- Identificamos no transferidor o ponto (C) correspondente à medida de 50º.
- Traçamos a semi-reta
, obtendo o ângulo BÂC que mede 50º.
Os ângulos de 30º, 45º, 60º e 90º são ângulos especiais.
Eles podem ser desenhados com esquadro.
TRANSFORMAÇÃO DE UNIDADES
Como vimos, quando trabalhamos com medidas de ângulos, utilizamos o sistema sexagesimal.
Observe nos exemplos como efetuar transformações nesse sistema:
- Transforme 30º em minutos.
Solução
Sendo 1º = 60', temos:
30º = 30 . 60'= 1.800
'Logo, 30º = 1.800
- Transforme 5º35' em minutos.
Solução
5º = 5 . 60' = 300'
300' + 35'= 335'
Logo, 5º35'= 335'.
- transforme 8º em segundos.
Solução
Sendo 1º = 60', temos:
8º = 8 . 60'= 480
'Sendo 1'= 60'', temos:
480'= 480 . 60'' = 28.800''
Logo, 8º = 28.800''.
- Transforme 3º35' em segundos.
Solução
3º = 3 . 60'= 180'
180' + 35' = 215'
215' . 60'' = 12.900''
Logo, 3º35'= 12.900''
- Transforme 2º20'40'' em segundos.
Solução
2º = 2 . 60' = 120'
120' + 20' = 140'
140'. 60''= 8.400''
8.400'' + 40'' = 8.440''
Logo, 2º20'40'' = 8.440''
Transformando uma medida de ângulo em número misto
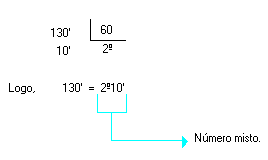
- Transforme 130' em graus e minutos.
Solução
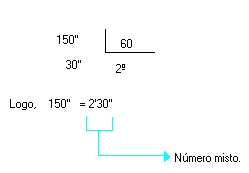
- Transforme 150'' em minutos e segundos.
Solução
- Transforme 26.138'' em graus, minutos e segundos.
Solução
Medidas fracionárias de um ângulo
- Transforme 24,5º em graus e minutos.
solução
0,5º = 0,5 . 60' = 30'
24,5º= 24º + 0,5º = 24º30'
Logo, 24,5º = 24º30'.
- Transforme 45º36' em graus.
solução
60' 
1º
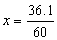
1º 36' x 
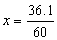
x x = 0,6º (lê-se ''seis décimos de grau'')
Logo, 45º36'= 45º + 0,6º = 45,6º.
- Transforme 5'54'' em minutos.
Solução
60'' 1'
1' 54'' x 
x x = 0,9' ( lê-se ''nove décimos de minuto'')
Logo, 5'54'' = 5'+ 0,9'= 5,9' OPERAÇÕES COM MEDIDAS DE ÂNGULOS
Observe alguns exemplos de como adicionar medidas de ângulos:
Adição
 |
 |
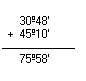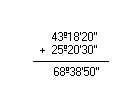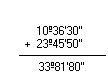 Simplificando 33º81'80'', obtemos:  Logo, a soma é 34º22'20''. | |
Observe os exemplos:
- 70º25' - 30º15
- 38º45'50'' - 27º32'35''
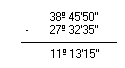
- 90º - 35º49'46''
- 80º48'30'' - 70º58'55''
Logo, a diferença é 9º 49'35''.
Multiplicação por um número natural
Observe os exemplos:
 |
 |
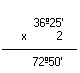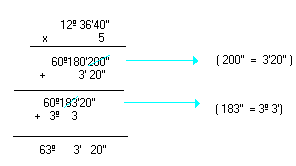 Logo, o produto é 63º3'20''. | |
Observe os exemplos:
|
|
|
- Geometria
Estudando Ãngulos Estudando os ângulos Ângulo é a abertura formada entre duas semirretas de mesma origem. Observe:A unidade de representação do ângulo é o grau (º). Classificamos um ângulo em agudo, reto ou obtuso. Ângulo reto:...
- Ângulos
Denominamos ângulo a região do plano limitada por duas semirretas de mesma origem. As semirretas recebem o nome de lados do ângulo e a origem delas, de vértice do ângulo. A unidade usual de medida de ângulo, de acordo com o sistema de medidas,...
- Ângulos
Ângulo é a reunião de duas semi-retas de mesma origem e não-colineares. Na figura Indicação do ângulo: AÔB, ou BÔA ou simplismente Ô PONTOS INTERNOS E PONTOS EXTERNOS A UM ÂNGULO Seja o ângulo AÔB MEDIDA DE UM ÂNGULO Um ângulo...
- Ângulos
Ângulo é a reunião de duas semi-retas de mesma origem e não-colineares. Na figura Indicação do ângulo: AÔB, ou BÔA ou simplismente Ô PONTOS INTERNOS E PONTOS EXTERNOS A UM ÂNGULO Seja o ângulo AÔB MEDIDA DE UM ÂNGULO Um...
- Ângulos
Ângulo é a reunião de duas semi-retas de mesma origem e não-colineares. Na figura Indicação do ângulo: AÔB, ou BÔA ou simplismente Ô PONTOS INTERNOS E PONTOS EXTERNOS A UM ÂNGULO Seja o ângulo AÔB MEDIDA DE UM ÂNGULO Um...