Matemática
O coeficiente angular será igual a m = tg 45° = 1. Um dos seus pontos será (0,0) e todos os outros pontos pertencentes à reta b terão as ordenadas e abscissas iguais, por exemplo, (4,4), (5,5), (6,6), (7,7),... .
Considerando qualquer um desses pontos e o coeficiente angular igual a 1, podemos concluir que a reta que representa a bissetriz dos quadrantes ímpares terá - de acordo com os conceitos de Geometria Analítica - a equação fundamental: y – y0 = m (x – x0).
Substituindo o ponto (2,2), temos:
y – 2 = 1 (x – 2)
y – 2 = x – 2
y = x
Bissetriz dos quadrantes pares
A bissetriz dos quadrantes pares é determinada por uma reta que intercepta o ponto (0,0) traçando as bissetrizes dos quadrantes II e IV.
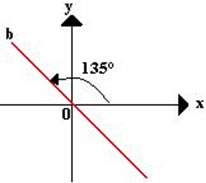
O coeficiente angular será igual a m = tg 135° = -1. Um dos seus pontos será (0,0) e todos os outros pontos pertencentes à reta b terão os valores das ordenadas opostos aos valores das abscissas, por exemplo, (4,-4), (5,-5), (6,-6), (7,-7),... .
Considerando qualquer um desses pontos e o coeficiente angular igual a -1, podemos concluir que a reta que representa a bissetriz dos quadrantes pares terá - de acordo com os conceitos de Geometria Analítica - a equação fundamental: y – y0 = m (x – x0).
y – (–2) = –1 (x – 2)
y + 2 = –x + 2
y = – xPor Marcos Noé
- Questão 73 ? Prova Do Estado ? (ofa) 2.012 ? Professor De Educação Básica Ii
A sentença que representa a bissetriz dos quadrantes pares de um sistema cartesiano ortogonal é: (A) x = y.(B) 3 ? x = 2 ? y.(C) 2 ? x = y.(D) x = 3 ? y.(E) x = ? y. Solução: (E) No plano cartesiano os quadrantes pares são: o quadrante II onde o...
- Introdução à Geometria Analítica
Para começar o estudo da geometria analítica, é necessário conhecer o Plano Cartesiano: O Eixo Y (linha vertical) é chamado de eixo das ordenadas, enquanto que o Eixo X (linha horizontal), é chamado de eixo das abscissas. O ponto P (ponto vermelho...
- Função
Chama-se polinomial toda função cuja lei que associa x à imagem de x é um polinômio. Por exemplo, são polinomiais as funções de definidas por: - f(x) = x3 – 5x2 + 3x + 1 - g(x) = x5 - h(x) = 3x + 1 Função polinomial de 1º grau Definição...
- Equação Fundamental Da Reta
Podemos determinar a equação fundamental de uma reta utilizando o ângulo formado pela reta com o eixo das abscissas (x) e as coordenadas de um ponto pertencente à reta. O coeficiente angular da reta, associado à coordenada do ponto, facilita a representação...
- Equação Fundamental Da Reta
Podemos determinar a equação fundamental de uma reta utilizando o ângulo formado pela reta com o eixo das abscissas (x) e as coordenadas de um ponto pertencente à reta. O coeficiente angular da reta, associado à coordenada do ponto, facilita a representação...
Matemática
As bissetrizes dos quadrantes
O plano cartesiano é formado por dois eixos perpendiculares que se cruzam na origem das coordenadas (0,0), estabelecendo quatro quadrantes. A intersecção perpendicular dos eixos forma ângulos de 90º.
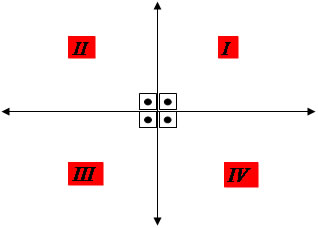

No plano cartesiano, ao traçarmos uma reta, que passa pelo ponto (0,0) formando um ângulo de 45º com a abscissa (eixo horizontal), estamos dividindo um quadrante ao meio e determinando a sua bissetriz.
Podemos traçar as bissetrizes dos quadrantes de duas formas: bissetriz dos quadrantes pares e bissetriz dos quadrantes ímpares.
Bissetriz dos quadrantes ímpares
A bissetriz dos quadrantes ímpares é determinada por uma reta que intercepta o ponto (0,0) traçando as bissetrizes dos quadrantes I e III.
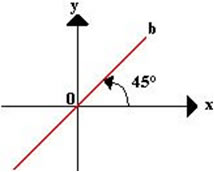
Podemos traçar as bissetrizes dos quadrantes de duas formas: bissetriz dos quadrantes pares e bissetriz dos quadrantes ímpares.
Bissetriz dos quadrantes ímpares
A bissetriz dos quadrantes ímpares é determinada por uma reta que intercepta o ponto (0,0) traçando as bissetrizes dos quadrantes I e III.

O coeficiente angular será igual a m = tg 45° = 1. Um dos seus pontos será (0,0) e todos os outros pontos pertencentes à reta b terão as ordenadas e abscissas iguais, por exemplo, (4,4), (5,5), (6,6), (7,7),... .
Considerando qualquer um desses pontos e o coeficiente angular igual a 1, podemos concluir que a reta que representa a bissetriz dos quadrantes ímpares terá - de acordo com os conceitos de Geometria Analítica - a equação fundamental: y – y0 = m (x – x0).
Substituindo o ponto (2,2), temos:
y – 2 = 1 (x – 2)
y – 2 = x – 2
y = x
Bissetriz dos quadrantes pares
A bissetriz dos quadrantes pares é determinada por uma reta que intercepta o ponto (0,0) traçando as bissetrizes dos quadrantes II e IV.

O coeficiente angular será igual a m = tg 135° = -1. Um dos seus pontos será (0,0) e todos os outros pontos pertencentes à reta b terão os valores das ordenadas opostos aos valores das abscissas, por exemplo, (4,-4), (5,-5), (6,-6), (7,-7),... .
Considerando qualquer um desses pontos e o coeficiente angular igual a -1, podemos concluir que a reta que representa a bissetriz dos quadrantes pares terá - de acordo com os conceitos de Geometria Analítica - a equação fundamental: y – y0 = m (x – x0).
y – (–2) = –1 (x – 2)
y + 2 = –x + 2
y = – x
- Questão 73 ? Prova Do Estado ? (ofa) 2.012 ? Professor De Educação Básica Ii
A sentença que representa a bissetriz dos quadrantes pares de um sistema cartesiano ortogonal é: (A) x = y.(B) 3 ? x = 2 ? y.(C) 2 ? x = y.(D) x = 3 ? y.(E) x = ? y. Solução: (E) No plano cartesiano os quadrantes pares são: o quadrante II onde o...
- Introdução à Geometria Analítica
Para começar o estudo da geometria analítica, é necessário conhecer o Plano Cartesiano: O Eixo Y (linha vertical) é chamado de eixo das ordenadas, enquanto que o Eixo X (linha horizontal), é chamado de eixo das abscissas. O ponto P (ponto vermelho...
- Função
Chama-se polinomial toda função cuja lei que associa x à imagem de x é um polinômio. Por exemplo, são polinomiais as funções de definidas por: - f(x) = x3 – 5x2 + 3x + 1 - g(x) = x5 - h(x) = 3x + 1 Função polinomial de 1º grau Definição...
- Equação Fundamental Da Reta
Podemos determinar a equação fundamental de uma reta utilizando o ângulo formado pela reta com o eixo das abscissas (x) e as coordenadas de um ponto pertencente à reta. O coeficiente angular da reta, associado à coordenada do ponto, facilita a representação...
- Equação Fundamental Da Reta
Podemos determinar a equação fundamental de uma reta utilizando o ângulo formado pela reta com o eixo das abscissas (x) e as coordenadas de um ponto pertencente à reta. O coeficiente angular da reta, associado à coordenada do ponto, facilita a representação...
