Matemática
O que vamos relembrar já foi exposto no texto “Divisão de polinômio por monômio”, mas vamos rever novamente: em toda divisão temos o dividendo, divisor, quociente e resto, como estamos falando de divisão de polinômio por polinômio, teremos:
Para o dividendo um polinômio G(x)
Para o divisor um polinômio D(x)
Para o quociente um polinômio Q(x)Para o resto (podendo ser zero) um polinômio R(x)

Prova real:
Tem algumas observações a serem feitas, como:
► ao final da divisão o resto sempre tem que ser menor que o divisor: R(x) < D(x).
► quando o resto for igual a zero, a divisão é considerada exata, ou seja, o dividendo é divisível pelo divisor. R(x) = 0.
Observe a divisão de polinômio por polinômio abaixo, vamos partir de um exemplo, cada passo tomado no desenvolvimento da divisão será explicado.
Dada a divisão
(12x3 + 9 – 4x) : (x + 2x2 + 3)
Antes de começar a operação temos que fazer algumas verificações:
► se todos os polinômios estão em ordem conforme as potências de x.
No caso da nossa divisão devemos ordenar, ficando assim:
(12x3 - 4x + 9) : (2x2 + x + 3)
► observar se no polinômio G(x) não está faltando algum termo, se estiver devemos completar.
No polinômio 12x3 - 4x + 9 está faltando o termo x2, completando ficará, assim:
12x3 + 0x2 - 4x + 9
Agora podemos iniciar a divisão:

► G(x) tem 3 termos e D(x) tem 3 termos. Pegamos o 1º termo de G(x) e dividimos pelo 1º termo de D(x): 12x3 : 2x2 = 6x, o resultado multiplicará o polinômio 2x2 + x + 3 e o resultado dessa multiplicação subtrairemos pelo polinômio 12x3 + 0x2 - 4x + 9. Assim teremos:


► R(x) > D(x), podemos dar continuidade à divisão, repetindo o mesmo processo anterior. Achando agora o segundo termo de Q(x).
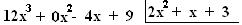

R(x) < D(x), não damos continuidade a divisão, concluindo que:
O quociente é 6x – 3 e o resto é –19x + 18.
Por Danielle de Miranda
Graduada em Matemática
- Divisão De Polinômios
Polinômio é uma expressão algébrica composta por dois ou mais monômios. Na divisão de polinômios, utilizamos duas regras matemáticas fundamentais: realizar a divisão entre os coeficientes numéricos e divisão de potências de mesma base (conservar...
- Polinômios
01. Calcular o valor numérico do polinômio P(x) = x3 - 7x2 + 3x - 4 para x = 2. RESOLUÇÃO: P(2) = -18 02. Determinar os valores reais de a e b para que o polinômio x3 + 6x2 + ax + b seja um cubo perfeito. RESOLUÇÃO: a = 12 e b = 8 03. (UESB)...
- Teorema De D’alembert
O teorema de D’Alembert é uma consequência imediata do teorema do resto, que são voltados para a divisão de polinômio por binômio do tipo x – a. O teorema do resto diz que um polinômio G(x) dividido por um binômio x – a terá resto R igual...
- Divisão De Polinômios
A operação de divisões é composta por dividendo, divisor, quociente e resto, no caso da divisão de polinômio por polinômio, considerando que cada um deles seja formado por mais de um monômio, iremos considerar a seguinte divisão: P(x) |G(x) R(x)...
- Divisão De Polinômio Por Polinômio
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
Matemática
Divisão inteira de polinómios
O que vamos relembrar já foi exposto no texto “Divisão de polinômio por monômio”, mas vamos rever novamente: em toda divisão temos o dividendo, divisor, quociente e resto, como estamos falando de divisão de polinômio por polinômio, teremos:
Para o dividendo um polinômio G(x)
Para o divisor um polinômio D(x)
Para o quociente um polinômio Q(x)Para o resto (podendo ser zero) um polinômio R(x)
Prova real:
Tem algumas observações a serem feitas, como:
► ao final da divisão o resto sempre tem que ser menor que o divisor: R(x) < D(x).
► quando o resto for igual a zero, a divisão é considerada exata, ou seja, o dividendo é divisível pelo divisor. R(x) = 0.
Observe a divisão de polinômio por polinômio abaixo, vamos partir de um exemplo, cada passo tomado no desenvolvimento da divisão será explicado.
Dada a divisão
(12x3 + 9 – 4x) : (x + 2x2 + 3)
Antes de começar a operação temos que fazer algumas verificações:
► se todos os polinômios estão em ordem conforme as potências de x.
No caso da nossa divisão devemos ordenar, ficando assim:
(12x3 - 4x + 9) : (2x2 + x + 3)
► observar se no polinômio G(x) não está faltando algum termo, se estiver devemos completar.
No polinômio 12x3 - 4x + 9 está faltando o termo x2, completando ficará, assim:
12x3 + 0x2 - 4x + 9
Agora podemos iniciar a divisão:

► G(x) tem 3 termos e D(x) tem 3 termos. Pegamos o 1º termo de G(x) e dividimos pelo 1º termo de D(x): 12x3 : 2x2 = 6x, o resultado multiplicará o polinômio 2x2 + x + 3 e o resultado dessa multiplicação subtrairemos pelo polinômio 12x3 + 0x2 - 4x + 9. Assim teremos:

► R(x) > D(x), podemos dar continuidade à divisão, repetindo o mesmo processo anterior. Achando agora o segundo termo de Q(x).
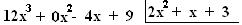

R(x) < D(x), não damos continuidade a divisão, concluindo que:
O quociente é 6x – 3 e o resto é –19x + 18.
Por Danielle de Miranda
Graduada em Matemática
- Divisão De Polinômios
Polinômio é uma expressão algébrica composta por dois ou mais monômios. Na divisão de polinômios, utilizamos duas regras matemáticas fundamentais: realizar a divisão entre os coeficientes numéricos e divisão de potências de mesma base (conservar...
- Polinômios
01. Calcular o valor numérico do polinômio P(x) = x3 - 7x2 + 3x - 4 para x = 2. RESOLUÇÃO: P(2) = -18 02. Determinar os valores reais de a e b para que o polinômio x3 + 6x2 + ax + b seja um cubo perfeito. RESOLUÇÃO: a = 12 e b = 8 03. (UESB)...
- Teorema De D’alembert
O teorema de D’Alembert é uma consequência imediata do teorema do resto, que são voltados para a divisão de polinômio por binômio do tipo x – a. O teorema do resto diz que um polinômio G(x) dividido por um binômio x – a terá resto R igual...
- Divisão De Polinômios
A operação de divisões é composta por dividendo, divisor, quociente e resto, no caso da divisão de polinômio por polinômio, considerando que cada um deles seja formado por mais de um monômio, iremos considerar a seguinte divisão: P(x) |G(x) R(x)...
- Divisão De Polinômio Por Polinômio
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
