Matemática

Torricelli
Evangelista Torricelli nasceu em Faenza, Itália. Foi físico e matemático que teve grandes e importantes contribuições na física e matemática. Inventou o barômetro, aperfeiçoou o telescópio e inventou um telescópio bem rudimentar. Na área da matemática ele, entre tantas outras descobertas, determinou o cálculo que possibilita calcular o centro de gravidade de qualquer figura geométrica por meio de duas integrais.
Integração é uma das operações básicas do cálculo, que apesar de ser uma operação matemática, também é muito utilizada na física.
Torricelli se formou em um colégio jesuíta, e na Universidade de Roma foi aluno de Bonaventura Cavalieri. Escreveu um tratado sobre mecânica, De moto gravium naturaliter descendentim et projectorum, que fala sobre os movimentos dos corpos ascendentes e projetados. Nesse tratado ele faz um brilhante comentário ao terceiro diálogo dos discursos de Galileu. Foi aluno, secretário e assistente de Galileu, cientista esse que teve grande influência na vida de Torricelli.
Após a morte de Galileu, Evangelista Torricelli foi nomeado grão-duque e professor de matemática na Academia Florentina. Ao retomar uma idéia de Galileu, Torricelli realizou experimentos com o tubo de mercúrio, e pela primeira vez conseguiu fazer o vácuo. Após seus estudos, com base nesse mesmo experimento, ele concluiu que as variações na coluna de mercúrio são provocadas pela influência da pressão atmosférica. Com isso ele acabava de inventar o barômetro de mercúrio, que a princípio se chamava “Tubo de Torricelli”. Formulou ainda, no mesmo ano que inventou o barômetro, a lei sobre o escoamento de líquidos.
Torricelli se tornou muito famoso também pela descoberta de um sólido infinitamente longo, que hoje é chamado de Trombeta de Gabriel, cuja área superficial é infinita e o seu volume, em contrapartida, é finito. Na época da descoberta essa propriedade foi vista como um grande paradoxo pelos contemporâneos, até mesmo por Torricelli que tentou demonstrações alternativas. Tal descoberta chegou a gerar questionamentos sobre a natureza do infinito.
Apesar de todas as suas descobertas, Torricelli é mais lembrado por descobrir uma equação matemática que possibilita calcular a velocidade de um determinado corpo sem o conhecimento do intervalo de tempo que o mesmo permaneceu em movimento. Essa equação pode ser escrita da seguinte forma:
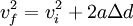
Onde:
Vf é a velocidade final;
Vi é a velocidade inicial;
a é a aceleração;
Δd é a variação de posição.
Tal equação pode ser utilizada para se calcular a velocidade do corpo que descreve movimento retilíneo uniformemente variado (MRUV), sem que se saiba por quanto tempo o móvel está em movimento.
www.mundoeducacao.com.br
- Cinemática -b Movimento Uniformemente Variado E Equação De Torricelli
Considere um movimento em que a velocidade do móvel varia, ou seja, o móvel tem aceleração. Se essa aceleração for constante, dizemos que esse móvel está executando um movimento uniformemente variado. Um exemplo clássico desse tipo de movimento...
- Movimento Uniformemente Variado
O movimento uniformemente variado é o movimento no qual a velocidade escalar varia uniformemente no decorrer do tempo. Quando se observa que a velocidade de uma partícula é uniforme, independentemente de sua trajetória, diz-se que a partícula possui...
- Equação De Torricelli
Sabendo que: Podemos isolar o tempo e obtemos: Substituindo este tempo em: Obtemos: Multiplicando a equação por 2a, temos: Que é a equação de Torricelli. Note que esta equação não depende do tempo. Veja Mais: Movimento Unidimensional...
- Aceleração
A aceleração é a taxa de variação da velocidade em relação ao tempo. Analogamente à velocidade instantânea, temos: Ou seja, a aceleração instantânea é a derivada em relação ao tempo da velocidade instantânea: que é a derivada segunda...
- Velocidade Instantânea
Enquanto a velocidade média é tomada num intervalo de tempo Δt, a velocidade instantânea é tomada num instante extremamente pequeno. Em termos mais rigorosos: Veja Mais: Movimento Unidimensional Transformação de Km/h em m/s Movimento...
Matemática
Equação de Torricelli

Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email [email protected]
www.ensinodematemtica.blogspot.com.br
www.accbarrosogestar.blogspot.com.br
WWW.profantoniocarneiro.com
Torricelli
Evangelista Torricelli nasceu em Faenza, Itália. Foi físico e matemático que teve grandes e importantes contribuições na física e matemática. Inventou o barômetro, aperfeiçoou o telescópio e inventou um telescópio bem rudimentar. Na área da matemática ele, entre tantas outras descobertas, determinou o cálculo que possibilita calcular o centro de gravidade de qualquer figura geométrica por meio de duas integrais.
Integração é uma das operações básicas do cálculo, que apesar de ser uma operação matemática, também é muito utilizada na física.
Torricelli se formou em um colégio jesuíta, e na Universidade de Roma foi aluno de Bonaventura Cavalieri. Escreveu um tratado sobre mecânica, De moto gravium naturaliter descendentim et projectorum, que fala sobre os movimentos dos corpos ascendentes e projetados. Nesse tratado ele faz um brilhante comentário ao terceiro diálogo dos discursos de Galileu. Foi aluno, secretário e assistente de Galileu, cientista esse que teve grande influência na vida de Torricelli.
Após a morte de Galileu, Evangelista Torricelli foi nomeado grão-duque e professor de matemática na Academia Florentina. Ao retomar uma idéia de Galileu, Torricelli realizou experimentos com o tubo de mercúrio, e pela primeira vez conseguiu fazer o vácuo. Após seus estudos, com base nesse mesmo experimento, ele concluiu que as variações na coluna de mercúrio são provocadas pela influência da pressão atmosférica. Com isso ele acabava de inventar o barômetro de mercúrio, que a princípio se chamava “Tubo de Torricelli”. Formulou ainda, no mesmo ano que inventou o barômetro, a lei sobre o escoamento de líquidos.
Torricelli se tornou muito famoso também pela descoberta de um sólido infinitamente longo, que hoje é chamado de Trombeta de Gabriel, cuja área superficial é infinita e o seu volume, em contrapartida, é finito. Na época da descoberta essa propriedade foi vista como um grande paradoxo pelos contemporâneos, até mesmo por Torricelli que tentou demonstrações alternativas. Tal descoberta chegou a gerar questionamentos sobre a natureza do infinito.
Apesar de todas as suas descobertas, Torricelli é mais lembrado por descobrir uma equação matemática que possibilita calcular a velocidade de um determinado corpo sem o conhecimento do intervalo de tempo que o mesmo permaneceu em movimento. Essa equação pode ser escrita da seguinte forma:
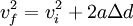
Onde:
Vf é a velocidade final;
Vi é a velocidade inicial;
a é a aceleração;
Δd é a variação de posição.
Tal equação pode ser utilizada para se calcular a velocidade do corpo que descreve movimento retilíneo uniformemente variado (MRUV), sem que se saiba por quanto tempo o móvel está em movimento.
www.mundoeducacao.com.br
- Cinemática -b Movimento Uniformemente Variado E Equação De Torricelli
Considere um movimento em que a velocidade do móvel varia, ou seja, o móvel tem aceleração. Se essa aceleração for constante, dizemos que esse móvel está executando um movimento uniformemente variado. Um exemplo clássico desse tipo de movimento...
- Movimento Uniformemente Variado
O movimento uniformemente variado é o movimento no qual a velocidade escalar varia uniformemente no decorrer do tempo. Quando se observa que a velocidade de uma partícula é uniforme, independentemente de sua trajetória, diz-se que a partícula possui...
- Equação De Torricelli
Sabendo que: Podemos isolar o tempo e obtemos: Substituindo este tempo em: Obtemos: Multiplicando a equação por 2a, temos: Que é a equação de Torricelli. Note que esta equação não depende do tempo. Veja Mais: Movimento Unidimensional...
- Aceleração
A aceleração é a taxa de variação da velocidade em relação ao tempo. Analogamente à velocidade instantânea, temos: Ou seja, a aceleração instantânea é a derivada em relação ao tempo da velocidade instantânea: que é a derivada segunda...
- Velocidade Instantânea
Enquanto a velocidade média é tomada num intervalo de tempo Δt, a velocidade instantânea é tomada num instante extremamente pequeno. Em termos mais rigorosos: Veja Mais: Movimento Unidimensional Transformação de Km/h em m/s Movimento...
