Matemática
http://accbarrosogestar.blogspot.com.br
- Equações Modulares
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso Colégio Estadual Dinah Gonçalves email [email protected] HTTP://ensinodematemtica.blogspot.com http://accbarrosogestar.blogspot.com.br Equações modularesTipos e estratégias...
- Equações Modulares
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
- Equações Modulares
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
- Equação Modular
Utilizando a definição de módulo que diz: | x | = x, se x for maior ou igual a zero. | x | = – x, se x for menor que zero. Podemos resolver equações modulares, uma vez que: Se | x | = k, então x = k ou x = – k. Exemplo 1. Resolva a equação...
- Equaçao Modular
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
Matemática
Equações modulares
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email [email protected]
Blog HTTP://ensinodematemtica.blogspot.comhttp://accbarrosogestar.blogspot.com.br
Equações modulares
Tipos e estratégias de resolução
Sabemos que
Uma equação modular é aquela em que a incógnita "aparece dentro do módulo".
Vamos aqui apresentar alguns tipos de equações e suas estratégias de resolução.
Exemplo 1
O que queremos aqui é saber qual é o número cujo módulo é igual a 5. Segundo a definição de módulo, esse número pode ser 5 ou -5, pois ambos têm módulo igual a 5.
Assim, podemos dizer que "desmembramos" a equação em duas, para "tirarmos" o módulo.
Exemplo 2
Da mesma forma, devemos desmembrar a equação.
Assim, se voltarmos à igualdade inicial e substituirmos x por -5 ou 3, ela será verdadeira:
Exemplo 3
Aqui também se desmembra a equação, com o devido cuidado quanto ao sinal da expressão do segundo membro da igualdade.
resolução.
Exemplo 1
O que queremos aqui é saber qual é o número cujo módulo é igual a 5. Segundo a definição de módulo, esse número pode ser 5 ou -5, pois ambos têm módulo igual a 5.
Assim, podemos dizer que "desmembramos" a equação em duas, para "tirarmos" o módulo.
Exemplo 2
Da mesma forma, devemos desmembrar a equação.
Assim, se voltarmos à igualdade inicial e substituirmos x por -5 ou 3, ela será verdadeira:
Exemplo 3
Logo, 0 e 2 são os valores que verificam as igualdades, quando colocados no lugar de x.
Exemplo 4
Nesse caso, queremos saber qual o valor de x para que a expressão tenha módulo igual a -5. Pela definição, sabemos que o módulo não pode ser igual a um número negativo. Logo, não existe tal valor de x.
Portanto,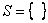 .
.
Exemplo 5
Exemplo 6
É bom lembrarmos uma das propriedades do módulo, segundo a qual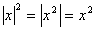 .
.
Logo, a equação pode ser reescrita da seguinte forma: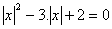 .
.
Agora, basta usar a técnica da substituição para facilitar a resolução.
Mas ainda não encontramos a solução da equação. Devemos voltar à substituição feita anteriormente.
Portanto, o conjunto solução da equação é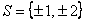 .
.
Exemplo 7
Se, para eliminar cada módulo, desmembrarmos em dois casos, teremos quatro equações, porém com dois pares de equações repetidas. Assim, para facilitarmos a resolução, consideraremos dois casos:
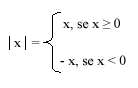 |
Uma equação modular é aquela em que a incógnita "aparece dentro do módulo".
Vamos aqui apresentar alguns tipos de equações e suas estratégias de resolução.
Exemplo 1
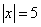 |
O que queremos aqui é saber qual é o número cujo módulo é igual a 5. Segundo a definição de módulo, esse número pode ser 5 ou -5, pois ambos têm módulo igual a 5.
Assim, podemos dizer que "desmembramos" a equação em duas, para "tirarmos" o módulo.
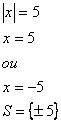 |
Exemplo 2
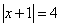 |
Da mesma forma, devemos desmembrar a equação.
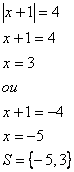 |
Assim, se voltarmos à igualdade inicial e substituirmos x por -5 ou 3, ela será verdadeira:
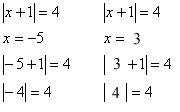 |
Exemplo 3
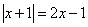 |
Aqui também se desmembra a equação, com o devido cuidado quanto ao sinal da expressão do segundo membro da igualdade.
resolução.
Exemplo 1
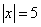 |
O que queremos aqui é saber qual é o número cujo módulo é igual a 5. Segundo a definição de módulo, esse número pode ser 5 ou -5, pois ambos têm módulo igual a 5.
Assim, podemos dizer que "desmembramos" a equação em duas, para "tirarmos" o módulo.
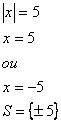 |
Exemplo 2
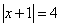 |
Da mesma forma, devemos desmembrar a equação.
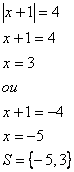 |
Assim, se voltarmos à igualdade inicial e substituirmos x por -5 ou 3, ela será verdadeira:
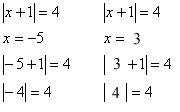 |
Exemplo 3
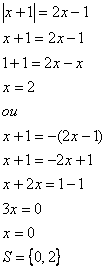 |
Logo, 0 e 2 são os valores que verificam as igualdades, quando colocados no lugar de x.
Exemplo 4
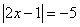 |
Nesse caso, queremos saber qual o valor de x para que a expressão tenha módulo igual a -5. Pela definição, sabemos que o módulo não pode ser igual a um número negativo. Logo, não existe tal valor de x.
Portanto,
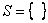 .
.Exemplo 5
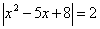 |
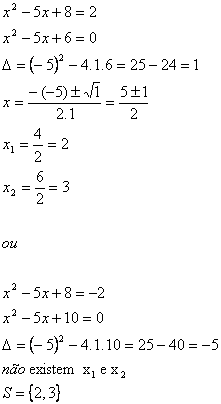 |
Exemplo 6
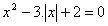 |
É bom lembrarmos uma das propriedades do módulo, segundo a qual
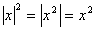 .
.Logo, a equação pode ser reescrita da seguinte forma:
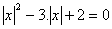 .
.Agora, basta usar a técnica da substituição para facilitar a resolução.
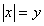 |
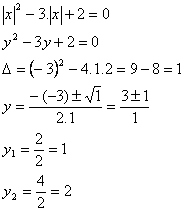 |
Mas ainda não encontramos a solução da equação. Devemos voltar à substituição feita anteriormente.
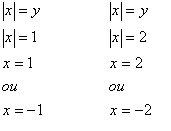 |
Portanto, o conjunto solução da equação é
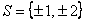 .
.Exemplo 7
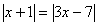 |
Se, para eliminar cada módulo, desmembrarmos em dois casos, teremos quatro equações, porém com dois pares de equações repetidas. Assim, para facilitarmos a resolução, consideraremos dois casos:
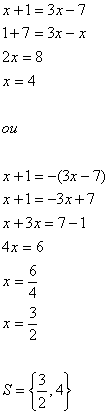 |
*Michele Viana Debus de França é licenciada em matemática pela USP e mestre em educação matemática pela PUC-SP.
- Equações Modulares
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso Colégio Estadual Dinah Gonçalves email [email protected] HTTP://ensinodematemtica.blogspot.com http://accbarrosogestar.blogspot.com.br Equações modularesTipos e estratégias...
- Equações Modulares
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
- Equações Modulares
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
- Equação Modular
Utilizando a definição de módulo que diz: | x | = x, se x for maior ou igual a zero. | x | = – x, se x for menor que zero. Podemos resolver equações modulares, uma vez que: Se | x | = k, então x = k ou x = – k. Exemplo 1. Resolva a equação...
- Equaçao Modular
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
