Matemática
- Post De Número 260
É com muita felicidade, que nós do Clave de Pi chgamos a marca de nosso post de numero 260. Agradecemos a todos que acessam nosso blog, pois sem vocês nada existiria. Também agradecemos a todos que comentam em nosso blog, aos nossos parceiros e todos...
- EquaÇÕes Incompletas Do 2º Grau
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos, como se resolvem as equações incompletas do 2º grau 1º CASO: Equação da forma ax² + c = 0 Exemplos: Resolver as seguintes equações,...
- Fatoração
Professor de Matemática no Colégio Estadual Dinah GonçalvesE Biologia na rede privada de Salvador-BahiaProfessor Antonio Carlos carneiro Barrosoemail [email protected] HTTP://ensinodematemtica.blogspot.com eHTTP://accbarroso60.wordpress.com...
- EquaÇÕes Incompletas Do 2º Grau
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos, como se resolvem as equações incompletas do 2º grau 1º CASO: Equação da forma ax² + c = 0 Exemplos: Resolver as seguintes equações,...
- EquaÇÕes Incompletas Do 2º Grau
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos, como se resolvem as equações incompletas do 2º grau 1º CASO: Equação da forma ax² + c = 0 Exemplos: Resolver as seguintes equações,...
Matemática
Função Modular
O valor absoluto de um número real é o próprio número real sem considerar o sinal, consequentemente não negativo.
Exemplos:
| + 7 | = 7 | – 4 | = 4 | 3 | = 3
| + 7 | = 7 | – 4 | = 4 | 3 | = 3
Sendo "a" um número real, | a | não pode ser igual a "a", pois se "a" fosse, por exemplo, –6, teria-se:
| – 6 | = – 6, o que estaria errado, mas se "a" fosse, por exemplo, 4, teria-se:
| 4 | = 4, que estaria certo.
Portanto, | a | = a, se "a" for positivo ou nulo e | a | = – a, se "a" for negativo.
| – 6 | = – 6, o que estaria errado, mas se "a" fosse, por exemplo, 4, teria-se:
| 4 | = 4, que estaria certo.
Portanto, | a | = a, se "a" for positivo ou nulo e | a | = – a, se "a" for negativo.
Uma função real onde a variável está em módulo (valor absoluto) é dita função modular.
f :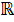

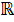
y = | f(x) |
f :
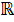

y = | f(x) |
Exemplos de função modular:
f(x) = | 2x + 4 |
g(x) = | x2 – 4x + 3 |
f(x) = | 2x + 4 |
g(x) = | x2 – 4x + 3 |
Representação gráfica
O gráfico de uma função modular pode ser esboçado mediante a separação em sentenças, por exemplo, dada a função f(x) = | 2 – x |.
Transformando-a em uma função de duas sentenças, cujo domínio real é dividido em duas condições (uma positiva ou nula e outra negativa).
Estudando o sinal da função que está em módulo, ou seja, achando a raiz da função que está no módulo, 2 – x = 0; e portanto x = 2.
Logo, tem-se:
f(x) > 0 quando x 2
2
f(x) = 0 quando x = 2 daí, f(x) = 2 – x, se x 2
2
f(x) < 0 quando x > 2 daí, f(x) = – 2 + x, se x > 2
f(x) =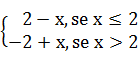
Assim, f(1) = 2 – 1 = 1 f(2) = 2 – 2 = 0 f(3) = – 2 + 3 = 1
Representando numa tabela tem-se:

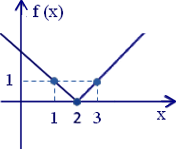
Transformando-a em uma função de duas sentenças, cujo domínio real é dividido em duas condições (uma positiva ou nula e outra negativa).
Estudando o sinal da função que está em módulo, ou seja, achando a raiz da função que está no módulo, 2 – x = 0; e portanto x = 2.
Logo, tem-se:
f(x) > 0 quando x
 2
2f(x) = 0 quando x = 2 daí, f(x) = 2 – x, se x
 2
2f(x) < 0 quando x > 2 daí, f(x) = – 2 + x, se x > 2
f(x) =
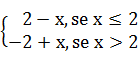
Assim, f(1) = 2 – 1 = 1 f(2) = 2 – 2 = 0 f(3) = – 2 + 3 = 1
Representando numa tabela tem-se:


Equação modular
Uma equação em que a incógnita esteja em módulo é chamada de equação modular.
Resolução:
Para resolver uma equação modular da forma | f(x) | = a, com "a" um número real negativo.
| 2x – 3 | = – 5, neste caso, a solução é vazio, pois nunca pode dar negativo.
S =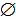
Para resolver uma equação modular da forma | f(x) | = 0.
| 2x – 3 | = 0, apenas a raiz é a solução, ou seja, 2x – 3 = 0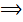 2x = 3 e daí, x = 3/2.
2x = 3 e daí, x = 3/2.
S = {3/2}
Para resolver uma equação modular da forma | f(x) | = a, com "a" um número real positivo.
| 2x – 3 | = 5, neste caso, separa | 2x – 3 | em dois casos: 2x – 3 = 5 ou – 2x + 3 = 5.
Para 2x – 3 = 5 tem-se: 2x – 8 = 0 e daí, x = 4.
Para – 2x + 3 = 5 tem-se: – 2x – 2 = 0 e daí, x = – 1.
S = { – 1; 4 }
Para resolver uma equação modular da forma | f(x) | = a, com "a" um número real negativo.
| 2x – 3 | = – 5, neste caso, a solução é vazio, pois nunca pode dar negativo.
S =
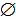
Para resolver uma equação modular da forma | f(x) | = 0.
| 2x – 3 | = 0, apenas a raiz é a solução, ou seja, 2x – 3 = 0
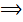 2x = 3 e daí, x = 3/2.
2x = 3 e daí, x = 3/2.S = {3/2}
Para resolver uma equação modular da forma | f(x) | = a, com "a" um número real positivo.
| 2x – 3 | = 5, neste caso, separa | 2x – 3 | em dois casos: 2x – 3 = 5 ou – 2x + 3 = 5.
Para 2x – 3 = 5 tem-se: 2x – 8 = 0 e daí, x = 4.
Para – 2x + 3 = 5 tem-se: – 2x – 2 = 0 e daí, x = – 1.
S = { – 1; 4 }
Inequação modular
Uma inequação em que a incógnita esteja em módulo é chamada de inequação modular.
Para resolver uma inequação modular da forma | f(x) | < 0.
| 2x – 3 | < 0, neste caso, a solução é vazio, pois nada que está em módulo pode ser negativo.
S =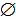
Para resolver uma inequação modular da forma | f(x) | 0.
0.
| 2x – 3 | = 0, apenas a raiz é a solução.
S = {3/2}
Para resolver uma inequação modular da forma | f(x) | > 0.
| 2x – 3 | > 0, neste caso, apenas a raiz não pertence a solução:
S = { x
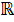 ; x
; x 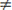 3/2 }
3/2 }
Para resolver uma inequação modular da forma | f(x) |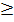 0.
0.
| 2x – 3 |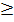 0, qualquer número real é válido.
0, qualquer número real é válido.
S =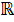
Para resolver uma inequação modular da forma | f(x) | < a ou | f(x) | a, com "a" um número real negativo.
a, com "a" um número real negativo.
| 2x – 3 | < – 5 ou | 2x – 3 | – 5, neste caso, a solução é vazio, pois nunca pode dar negativo.
– 5, neste caso, a solução é vazio, pois nunca pode dar negativo.
S =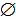
Para resolver uma inequação modular da forma | f(x) | < a, com "a" um número real positivo.
| 2x – 3 | < 5, neste caso, separa | 2x – 3 | em dois casos: 2x – 3 < 5 ou – 2x + 3 < 5.
Para 2x – 3 < 5 tem-se: 2x – 8 < 0 e daí, x < 4 (onde 2x – 8 é menor que zero, ou seja, negativo).
Para – 2x + 3 < 5 tem-se: – 2x – 2 < 0 e daí, x > – 1 (onde – 2x – 2 é menor que zero, ou seja, negativo).
S = { x
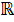 ; – 1 < x < 4 }
; – 1 < x < 4 }
Para resolver uma inequação modular da forma | f(x) | a, com "a" um número real positivo.
a, com "a" um número real positivo.
| 2x – 3 | 5, e a mesma situação anterior acrescentado o igual.
5, e a mesma situação anterior acrescentado o igual.
S = x
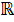 ; – 1
; – 1  x
x  4 }
4 }
Para resolver uma inequação modular da forma | f(x) | > a, com "a" um número real positivo.
| 2x – 3 | > 5, neste caso, separa | 2x – 3 | em dois casos: 2x – 3 > 5 ou – 2x + 3 > 5.
Para 2x – 3 > 5 tem-se: 2x – 8 > 0 e daí, x > 4 (onde 2x – 8 é maior que zero, ou seja, positivo).
Para – 2x + 3 > 5 tem-se: – 2x – 2 > 0 e daí, x < – 1 (onde – 2x – 2 é maior que zero, ou seja, positivo).
S = { x
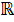 ; x < – 1 ou x > 4 }
; x < – 1 ou x > 4 }
Para resolver uma inequação modular da forma | f(x) |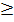 a, com "a" um número real positivo.
a, com "a" um número real positivo.
| 2x – 3 |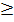 5, é a mesma situação anterior acrescentado o igual.
5, é a mesma situação anterior acrescentado o igual.
S = x
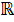 ; x
; x  – 1 ou x
– 1 ou x 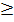 4 }
4 }
| 2x – 3 | < 0, neste caso, a solução é vazio, pois nada que está em módulo pode ser negativo.
S =
Para resolver uma inequação modular da forma | f(x) |
 0.
0.| 2x – 3 | = 0, apenas a raiz é a solução.
S = {3/2}
Para resolver uma inequação modular da forma | f(x) | > 0.
| 2x – 3 | > 0, neste caso, apenas a raiz não pertence a solução:
S = { x

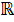 ; x
; x 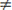 3/2 }
3/2 }Para resolver uma inequação modular da forma | f(x) |
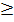 0.
0.| 2x – 3 |
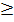 0, qualquer número real é válido.
0, qualquer número real é válido.S =
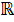
Para resolver uma inequação modular da forma | f(x) | < a ou | f(x) |
 a, com "a" um número real negativo.
a, com "a" um número real negativo.| 2x – 3 | < – 5 ou | 2x – 3 |
 – 5, neste caso, a solução é vazio, pois nunca pode dar negativo.
– 5, neste caso, a solução é vazio, pois nunca pode dar negativo.S =
Para resolver uma inequação modular da forma | f(x) | < a, com "a" um número real positivo.
| 2x – 3 | < 5, neste caso, separa | 2x – 3 | em dois casos: 2x – 3 < 5 ou – 2x + 3 < 5.
Para 2x – 3 < 5 tem-se: 2x – 8 < 0 e daí, x < 4 (onde 2x – 8 é menor que zero, ou seja, negativo).
Para – 2x + 3 < 5 tem-se: – 2x – 2 < 0 e daí, x > – 1 (onde – 2x – 2 é menor que zero, ou seja, negativo).
S = { x

 ; – 1 < x < 4 }
; – 1 < x < 4 }Para resolver uma inequação modular da forma | f(x) |
 a, com "a" um número real positivo.
a, com "a" um número real positivo.| 2x – 3 |
 5, e a mesma situação anterior acrescentado o igual.
5, e a mesma situação anterior acrescentado o igual.S = x

 ; – 1
; – 1  x
x  4 }
4 }Para resolver uma inequação modular da forma | f(x) | > a, com "a" um número real positivo.
| 2x – 3 | > 5, neste caso, separa | 2x – 3 | em dois casos: 2x – 3 > 5 ou – 2x + 3 > 5.
Para 2x – 3 > 5 tem-se: 2x – 8 > 0 e daí, x > 4 (onde 2x – 8 é maior que zero, ou seja, positivo).
Para – 2x + 3 > 5 tem-se: – 2x – 2 > 0 e daí, x < – 1 (onde – 2x – 2 é maior que zero, ou seja, positivo).
S = { x

 ; x < – 1 ou x > 4 }
; x < – 1 ou x > 4 }Para resolver uma inequação modular da forma | f(x) |
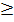 a, com "a" um número real positivo.
a, com "a" um número real positivo.| 2x – 3 |
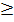 5, é a mesma situação anterior acrescentado o igual.
5, é a mesma situação anterior acrescentado o igual.S = x

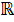 ; x
; x  – 1 ou x
– 1 ou x 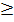 4 }
4 }Exercícios Resolvidos
R01 — Faça um Esboço gráfico de f(x) = | x – 1 |.
Encontrando a raiz: x – 1 = 0 então, a raiz é x = 1. Como a direita da raiz é positivo e a esquerda é negativo, vem que:
f(x) = x – 1, se x 1 e f(x) = – x + 1, se x < 1.
1 e f(x) = – x + 1, se x < 1.
f(x) =
Assim, f(0) = – 0 + 1 = 1, f(1) = 1 – 1 = 0, f(2) = 2 – 1 = 1.

f(x) = x – 1, se x
 1 e f(x) = – x + 1, se x < 1.
1 e f(x) = – x + 1, se x < 1.f(x) =

Assim, f(0) = – 0 + 1 = 1, f(1) = 1 – 1 = 0, f(2) = 2 – 1 = 1.


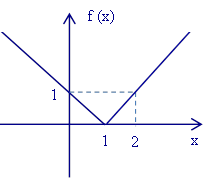
R02 — Faça um Esboço gráfico de f(x) = | x – 1 | + 1.
Como a raiz é x = 1 tem-se:
f(x) = x – 1 + 1 = x, se 1 e f(x) = – x + 1 + 1 = – x + 2, se x < 1.
1 e f(x) = – x + 1 + 1 = – x + 2, se x < 1.
f(x) =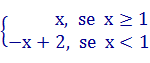
Assim, f(0) = – 0 + 2 = 2, f(1) = 1, f(2) = 2.

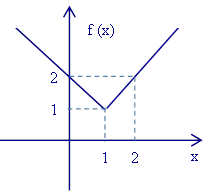
f(x) = x – 1 + 1 = x, se
 1 e f(x) = – x + 1 + 1 = – x + 2, se x < 1.
1 e f(x) = – x + 1 + 1 = – x + 2, se x < 1.f(x) =
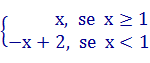
Assim, f(0) = – 0 + 2 = 2, f(1) = 1, f(2) = 2.


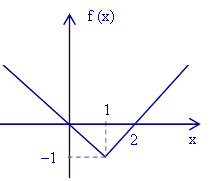
R03 — Faça um Esboço gráfico de f(x) = | x – 1 | – 1.
Como a raiz é x = 1 tem-se:
f(x) = x – 1 – 1 = x – 2, se 1 e f(x) = – x + 1 – 1 = – x, se x < 1.
1 e f(x) = – x + 1 – 1 = – x, se x < 1.
f(x) =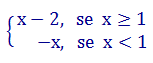
Assim, f(0) = – 0 = 0, f(1) = 1 – 2 = 0, f(2) = 2 – 2 = 0.

f(x) = x – 1 – 1 = x – 2, se
 1 e f(x) = – x + 1 – 1 = – x, se x < 1.
1 e f(x) = – x + 1 – 1 = – x, se x < 1.f(x) =
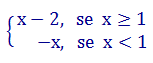
Assim, f(0) = – 0 = 0, f(1) = 1 – 2 = 0, f(2) = 2 – 2 = 0.


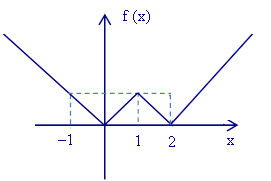
R04 — Esboçe o gráfico de f(x) = | | x – 1 | – 1 |.
Encontrando a raiz de | x – 1 | tem-se x = 1, então | x – 1 | = x – 1, se x  1 e | x – 1 | = – x + 1, se x < 1.
1 e | x – 1 | = – x + 1, se x < 1.
Então f(x) = | x – 1 – 1 | = | x – 2 |, se x 1 e f(x) = | – x + 1 – 1 = | – x |, se x < 1.
1 e f(x) = | – x + 1 – 1 = | – x |, se x < 1.
Para x 1:
1:
A raiz de x – 2 = 0 é x = 2 (que é positivo se x 2 e negativo se x < 2).
2 e negativo se x < 2).
f(x) = x – 2, se x 2 e f(x) = – x + 2, se 1
2 e f(x) = – x + 2, se 1 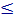 x < 2.
x < 2.
Para x < 1:
A raiz de – x = 0 é x = 0 (que é positivo quando x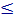 0 e negativo se x > 0).
0 e negativo se x > 0).
f(x) = – x se x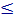 0 e f(x) = – (–x) = x, se 0 < x < 1.
0 e f(x) = – (–x) = x, se 0 < x < 1.
f(x) =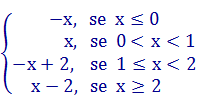
Assim, f(– 1) = – (– 1) = 1, f(0) = – 0 = 0, f(1) = – 1 + 2 = 1, f(2) = 2 – 2 = 0, f(3) = 3 – 2 = 1.
 1 e | x – 1 | = – x + 1, se x < 1.
1 e | x – 1 | = – x + 1, se x < 1.Então f(x) = | x – 1 – 1 | = | x – 2 |, se x
 1 e f(x) = | – x + 1 – 1 = | – x |, se x < 1.
1 e f(x) = | – x + 1 – 1 = | – x |, se x < 1.Para x
 1:
1:A raiz de x – 2 = 0 é x = 2 (que é positivo se x
 2 e negativo se x < 2).
2 e negativo se x < 2).f(x) = x – 2, se x
 2 e f(x) = – x + 2, se 1
2 e f(x) = – x + 2, se 1 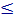 x < 2.
x < 2.Para x < 1:
A raiz de – x = 0 é x = 0 (que é positivo quando x
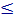 0 e negativo se x > 0).
0 e negativo se x > 0).f(x) = – x se x
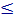 0 e f(x) = – (–x) = x, se 0 < x < 1.
0 e f(x) = – (–x) = x, se 0 < x < 1.f(x) =
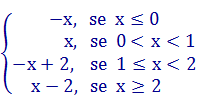
Assim, f(– 1) = – (– 1) = 1, f(0) = – 0 = 0, f(1) = – 1 + 2 = 1, f(2) = 2 – 2 = 0, f(3) = 3 – 2 = 1.

R05 — Resolva a equação | | 2x – 1 | – 3 | = 2.
Há duas opções para esta equação: ou | 2x – 1 | – 3 = 2 ou | 2x – 1 | – 3 = – 2.
Na primeira | 2x – 1 | = 2 + 3 = 5, o que dá duas opções: 2x – 1 = 5 e daí, 2x = 6 logo x = 3 ou 2x – 1 = – 5 e daí, 2x = – 4, logo x = – 2.
Na segunda | 2x – 1 | = – 2 + 3 = 1, o que também dá duas opções: 2x – 1 = 1 ou 2x – = – 1.
Em 2x – 1 = 1, tem-se x = 1 e em 2x – 1 = – 1, tem-se, x = 0.
Portanto, a solução é S = { – 2, 0, 1, 3 }.
Na primeira | 2x – 1 | = 2 + 3 = 5, o que dá duas opções: 2x – 1 = 5 e daí, 2x = 6 logo x = 3 ou 2x – 1 = – 5 e daí, 2x = – 4, logo x = – 2.
Na segunda | 2x – 1 | = – 2 + 3 = 1, o que também dá duas opções: 2x – 1 = 1 ou 2x – = – 1.
Em 2x – 1 = 1, tem-se x = 1 e em 2x – 1 = – 1, tem-se, x = 0.
Portanto, a solução é S = { – 2, 0, 1, 3 }.
R06 — Encontre a solução da inequação 6 > | x2 + 5x |.
Em | x2 + 5x | < 6, têm-se: x2 + 5x < 6 ou x2 + 5x > – 6
O que é o mesmo que resolver as inequações:
x2 + 5x – 6 < 0 ou x2 + 5x + 6 > 0
Para x2 + 5x – 6 = 0 tem-se:
x' = 1 e x'' = – 6
E como se deseja que x2 + 5x – 6 seja negativo, a solução é – 6 < x < 1.
Para x2 + 5x + 6 = 0 tem-se:
x' = – 2 e x'' = – 3
E como se deseja que x2 + 5x + 6 seja positivo, a solução é x < – 3 ou x > – 2.
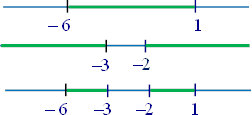
Logo a solução da inequação | x2 + 5x | < 6 é:
S = { x
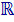 ; – 6 < x < – 3 ou – 2 < x < 1 }
; – 6 < x < – 3 ou – 2 < x < 1 }
O que é o mesmo que resolver as inequações:
x2 + 5x – 6 < 0 ou x2 + 5x + 6 > 0
Para x2 + 5x – 6 = 0 tem-se:
x' = 1 e x'' = – 6
E como se deseja que x2 + 5x – 6 seja negativo, a solução é – 6 < x < 1.
Para x2 + 5x + 6 = 0 tem-se:
x' = – 2 e x'' = – 3
E como se deseja que x2 + 5x + 6 seja positivo, a solução é x < – 3 ou x > – 2.

Logo a solução da inequação | x2 + 5x | < 6 é:
S = { x

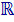 ; – 6 < x < – 3 ou – 2 < x < 1 }
; – 6 < x < – 3 ou – 2 < x < 1 }R07 — Calcule k de modo que a função (| 2k – 3 |)x2 + 5x – 3 seja do 2° grau.
Para ser do 2° grau, | 2k – 3 | 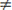 0 e, portanto, com exceção da raiz qualquer real serve.
0 e, portanto, com exceção da raiz qualquer real serve.
A raiz é 2k – 3 = 0, ou seja, k = 3/2. Então a solução é:
S = { k
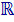 ; k
; k 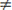 3/2 }
3/2 }
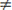 0 e, portanto, com exceção da raiz qualquer real serve.
0 e, portanto, com exceção da raiz qualquer real serve.A raiz é 2k – 3 = 0, ou seja, k = 3/2. Então a solução é:
S = { k

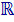 ; k
; k 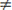 3/2 }
3/2 }R08 — Esboce um gráfico para a função modular dada por f(x) = | x + 2 | – | x + 1 |.
Em | x + 2 | se tem: x + 2, se x  – 2 e – x – 2, se x < – 2.
– 2 e – x – 2, se x < – 2.
Em | x + 1 | se tem: x + 1, se x – 1 e – x – 1, se x < – 1.
– 1 e – x – 1, se x < – 1.
Se x – 2 e x
– 2 e x  – 1 tem-se:
– 1 tem-se:
f(x) = x + 2 – ( x + 1 ) = x + 2 – x – 1 = 1, se x – 1.
– 1.
Se x – 2 e x < – 1 tem-se:
– 2 e x < – 1 tem-se:
f(x) = x + 2 – ( – x – 1 ) = x + 2 + x + 1 = 2x + 3, se – 2 x < – 1.
x < – 1.
Se x < – 2 e x – 1, não há intervalo comum.
– 1, não há intervalo comum.
Se x < – 2 e x < – 1 tem-se:
f(x) = – x – 2 – ( – x – 1 ) = – x – 2 + x + 1 = – 1, se x < – 2.
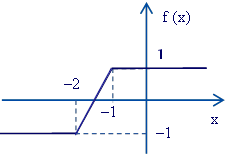
Assim, a lei de formação de f(x) é dada por:
f(x) =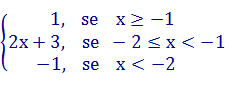
 – 2 e – x – 2, se x < – 2.
– 2 e – x – 2, se x < – 2.Em | x + 1 | se tem: x + 1, se x
 – 1 e – x – 1, se x < – 1.
– 1 e – x – 1, se x < – 1.Se x
 – 2 e x
– 2 e x  – 1 tem-se:
– 1 tem-se:f(x) = x + 2 – ( x + 1 ) = x + 2 – x – 1 = 1, se x
 – 1.
– 1.Se x
 – 2 e x < – 1 tem-se:
– 2 e x < – 1 tem-se:f(x) = x + 2 – ( – x – 1 ) = x + 2 + x + 1 = 2x + 3, se – 2
 x < – 1.
x < – 1.Se x < – 2 e x
 – 1, não há intervalo comum.
– 1, não há intervalo comum.Se x < – 2 e x < – 1 tem-se:
f(x) = – x – 2 – ( – x – 1 ) = – x – 2 + x + 1 = – 1, se x < – 2.
Assim, a lei de formação de f(x) é dada por:
f(x) =
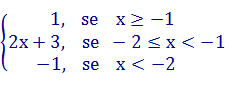

R09 — Dada a função f(x) = | k – 1 |x2 – x – 3. Determine k para que a função tenha raízes reais e distintas.
Para que raízes distintas 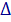 > 0, então:
> 0, então:
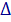 = (– 1)2 – 4 . | k – 1 | . (– 3) = 1 + 12 . | k – 1 |.
= (– 1)2 – 4 . | k – 1 | . (– 3) = 1 + 12 . | k – 1 |.
1 + 12 . | k – 1 | > 0 ou 12 . | k – 1 | > – 1 ou | k – 1 | > – 1/12
Como sempre o módulo é positivo, então qualquer que seja o k real é válido.
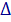 > 0, então:
> 0, então: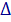 = (– 1)2 – 4 . | k – 1 | . (– 3) = 1 + 12 . | k – 1 |.
= (– 1)2 – 4 . | k – 1 | . (– 3) = 1 + 12 . | k – 1 |.1 + 12 . | k – 1 | > 0 ou 12 . | k – 1 | > – 1 ou | k – 1 | > – 1/12
Como sempre o módulo é positivo, então qualquer que seja o k real é válido.
R10 — As raízes da equação | x |2 + | x | – 6 = 0:
a) são positivas
b) tem soma igual a zero
c) tem soma igual a um
d) tem produto igual a seis
e) tem produto igual a menos seis
a) são positivas
b) tem soma igual a zero
c) tem soma igual a um
d) tem produto igual a seis
e) tem produto igual a menos seis
Substituindo | x | por "y" tem-se: y2 + y – 6 = 0, cujas raízes são y' = – 3 e y'' = 2.
Então | x | = – 3 ou | x | = 2
Como a primeira não tem solução, as únicas soluções são x = – 2 ou x = 2.
Alternativa "b".
Então | x | = – 3 ou | x | = 2
Como a primeira não tem solução, as únicas soluções são x = – 2 ou x = 2.
Alternativa "b".
R11 — Resolva a equação 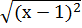 = 4.
= 4.
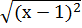 = 4.
= 4.Elevando ambos os membros ao quadrado têm-se:
(x – 1)2 = 16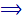 x – 1 = ± 4, e daí, x' = 5 e x'' = – 3.
x – 1 = ± 4, e daí, x' = 5 e x'' = – 3.
S = { – 3, 5 }
(x – 1)2 = 16
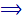 x – 1 = ± 4, e daí, x' = 5 e x'' = – 3.
x – 1 = ± 4, e daí, x' = 5 e x'' = – 3.S = { – 3, 5 }
Outra forma de resolver seria:
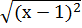 = | x – 1 | = 4, e daí, x – 1 = 4 ou x = 4 + 1 = 5 e x – 1 = – 4 ou x = – 4 + 1 = – 3.
= | x – 1 | = 4, e daí, x – 1 = 4 ou x = 4 + 1 = 5 e x – 1 = – 4 ou x = – 4 + 1 = – 3.
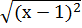 = | x – 1 | = 4, e daí, x – 1 = 4 ou x = 4 + 1 = 5 e x – 1 = – 4 ou x = – 4 + 1 = – 3.
= | x – 1 | = 4, e daí, x – 1 = 4 ou x = 4 + 1 = 5 e x – 1 = – 4 ou x = – 4 + 1 = – 3.R12 — Resolva a equação | 3 – 2x | = x + 3.
Neste caso, é necessário x + 3 > 0, ou seja, x > – 3.
3 – 2x = x + 3 ou – 3 + 2x = x + 3
3 – 3 = x + 2x ou 2x – x = 3 + 3
0 = 3x ou x = 6
Como ambos são maiores que – 3, então:
S = { 0, 6 }.
3 – 2x = x + 3 ou – 3 + 2x = x + 3
3 – 3 = x + 2x ou 2x – x = 3 + 3
0 = 3x ou x = 6
Como ambos são maiores que – 3, então:
S = { 0, 6 }.
Exercícios Propostos
P01 — Faça um esboço gráfico de f(x) = | 1 – 2x |.
P02 — Resolva a equação | 3 – 5x | = 1.
P03 — Represente graficamente a função y = | – x2 + 2x + 3 |.
P04 — Resolva a equação | 2 – 4x | = 3x – 5.
P05 — Resolva a inequação | 3x + 9 |  6.
6.
 6.
6.P06 — Esboce um gráfico para a função modular f(x) = | 2x – 6 | + | x – 3 |.
P07 — Resolva a equação 3| x |2 – | x | – 2 = 0.
P08 — Determine o valor de k para que o gráfico da função f(x) = ( | k2 – 4 | )x2 + x – 2 tenha a concavidade voltada para cima.
P09 — A soma das raízes da equação | x2 – 3x | = 2 é:
a) 3 b) 4 c) 5 d) 6 e) 7
a) 3 b) 4 c) 5 d) 6 e) 7
P10 — Encontre k para que a função f(x) = (| 2k – 1 | – 4)x + 7 seja crescente.
P11 — Determine k para que a função y = (| k | – 3)x2 – 5x + 6 tenha a concavidade voltada para baixo.
P12 — Encontre a solução de | 4 – 3x | > 2x – 1.
P13 — Obtenha o conjunto-solução de 
 0.
0.

 0.
0.P14 — Resolva a inequação: | x + 1 | – | 2 – x | < 0.
P15 — Encontre a solução de | x – 4 | = | 2x – 3 |.
P16 — Esboce um gráfico para a função modular dada por f(x) = | x + 2 | + | x + 1 |.
P17 — Considere a equação | x | = x – 6. Com respeito à solução real dessa equação, podemos afirmar que:
a) a solução pertence ao intervalo [ 1, 2 ]
b) a solução pertence ao intervalo [ –2, –1 ]
c) a solução pertence ao intervalo ] –1, 1 [
d) a equação não tem solução
a) a solução pertence ao intervalo [ 1, 2 ]
b) a solução pertence ao intervalo [ –2, –1 ]
c) a solução pertence ao intervalo ] –1, 1 [
d) a equação não tem solução
P18 — O maior valor que y pode assumir em y = 3 – | x – 3 | é:
a) 2 b) 3 c) 6 d) 9 e) 27
a) 2 b) 3 c) 6 d) 9 e) 27
P19 — Encontre k para que a função f(x) = (| 3k – 3| – 5)x + 7 seja do 1° grau.
P20 — Determine k para que a função y = (| 2k + 6 | – 6)x2 – 5x + 1 tenha a concavidade voltada para cima.
Fonte: http://hpdemat.apphb.com
- Post De Número 260
É com muita felicidade, que nós do Clave de Pi chgamos a marca de nosso post de numero 260. Agradecemos a todos que acessam nosso blog, pois sem vocês nada existiria. Também agradecemos a todos que comentam em nosso blog, aos nossos parceiros e todos...
- EquaÇÕes Incompletas Do 2º Grau
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos, como se resolvem as equações incompletas do 2º grau 1º CASO: Equação da forma ax² + c = 0 Exemplos: Resolver as seguintes equações,...
- Fatoração
Professor de Matemática no Colégio Estadual Dinah GonçalvesE Biologia na rede privada de Salvador-BahiaProfessor Antonio Carlos carneiro Barrosoemail [email protected] HTTP://ensinodematemtica.blogspot.com eHTTP://accbarroso60.wordpress.com...
- EquaÇÕes Incompletas Do 2º Grau
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos, como se resolvem as equações incompletas do 2º grau 1º CASO: Equação da forma ax² + c = 0 Exemplos: Resolver as seguintes equações,...
- EquaÇÕes Incompletas Do 2º Grau
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos, como se resolvem as equações incompletas do 2º grau 1º CASO: Equação da forma ax² + c = 0 Exemplos: Resolver as seguintes equações,...