Matemática
1 - FUNÇÃO INVERSA
Dada uma função f : A ® B , se f é bijetora , então define-se a função inversa f -1 como sendo a função de B em A , tal que f -1 (y) = x .
Veja a representação a seguir:

É óbvio então que:
a) para obter a função inversa , basta permutar as variáveis x e y .
b) o domínio de f -1 é igual ao conjunto imagem de f .
c) o conjunto imagem de f -1 é igual ao domínio de f .
d) os gráficos de f e de f -1 são curvas simétricas em relação à reta y = x ou seja , à bissetriz do primeiro quadrante .
Exemplo:Determine a INVERSA da função definida por y = 2x + 3.
Permutando as variáveis x e y, fica: x = 2y + 3
Explicitando y em função de x, vem:
2y = x - 3 \ y = (x - 3) / 2, que define a função inversa da função dada.
O gráfico abaixo, representa uma função e a sua inversa.
Observe que as curvas representativas de f e de f-1, são simétricas em relação à reta
y = x, bissetriz do primeiro e terceiro quadrantes.

Exercício resolvido:
A função f: R ® R , definida por f(x) = x2 :
a) é inversível e sua inversa é f -1 (x) = Ö x
b) é inversível e sua inversa é f -1(x) = - Ö x
c) não é inversível
d) é injetora
e) é bijetora
SOLUÇÃO:
Já sabemos que somente as funções bijetoras são inversíveis, ou seja, admitem função inversa. Ora, a função f(x) = x2, definida em R - conjunto dos números reais - não é injetora, pois elementos distintos possuem a mesma imagem. Por exemplo,
f(3) = f(-3) = 9. Somente por este motivo, a função não é bijetora e, em conseqüência, não é inversível.
Observe também que a função dada não é sobrejetora, pois o conjunto imagem da função f(x) = x2 é o conjunto R + dos números reais não negativos, o qual não coincide com o contradomínio dado que é
igual a R. A alternativa correta é a letra C.
2 - FUNÇÃO COMPOSTA
Chama-se função composta ( ou função de função ) à função obtida substituindo-se a variável independente x , por uma função.
Simbologia : fog (x) = f(g(x)) ou gof (x) = g(f(x)) .
Veja o esquema a seguir:
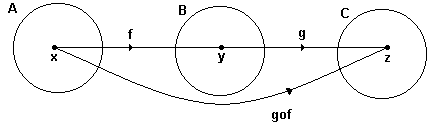
Obs : atente para o fato de que fog ¹ gof , ou seja, a operação " composição de funções " não é comutativa .
Exemplo:
Dadas as funções f(x) = 2x + 3 e g(x) = 5x, pede-se determinar gof(x) e fog(x).
Teremos:
gof(x) = g[f(x)] = g(2x + 3) = 5(2x + 3) = 10x + 15
fog(x) = f[g(x)] = f(5x) = 2(5x) + 3 = 10x + 3
Observe que fog ¹ gof .
Exercícios resolvidos:
1 - Sendo f e g duas funções tais que: f(x) = ax + b e g(x) = cx + d . Podemos afirmar que a igualdade gof(x) = fog(x) ocorrerá se e somente se:
a) b(1 - c) = d(1 - a)
b) a(1 - b) = d(1 - c)
c) ab = cd
d) ad = bc
e) a = bc
SOLUÇÃO:
Teremos:
fog(x) = f[g(x)] = f(cx + d) = a(cx + d) + b \ fog(x) = acx + ad + b
gof(x) = g[f(x)] = g(ax + b) = c(ax + b) + d \ gof(x) = cax + cb + d
Como o problema exige que gof = fog, fica:
acx + ad + b = cax + cb + d
Simplificando, vem:
ad + b = cb + d
ad - d = cb - b \ d(a - 1) = b(c - 1), que é equivalente a d(a - 1) = b(c - 1), o que nos leva a concluir que a alternativa correta é a letra A. .
2 - Sendo f e g duas funções tais que fog(x) = 2x + 1 e g(x) = 2 - x então f(x) é:
a) 2 - 2x
b) 3 - 3x
c) 2x - 5
*d) 5 - 2x
e) uma função par.
SOLUÇÃO:
Sendo fog(x) = 2x + 1, temos: f[g(x)] = 2x + 1
Substituindo g(x) pelo seu valor, fica: f(2 - x) = 2x + 1
Fazendo uma mudança de variável, podemos escrever 2 - x = u, sendo u a nova variável. Portanto, x = 2 - u.
Substituindo, fica:
f(u) = 2(2 - u) + 1 \ f(u) = 5 - 2u
Portanto, f(x) = 5 - 2x , o que nos leva à alternativa D.
Agora resolva esta:
Dadas as funções f(x) = 4x + 5 e g(x) = 2x - 5k, ocorrerá gof(x) = fog(x) se e somente se k for igual a:
*a) -1/3
b) 1/3
c) 0
d) 1
e) -1
- Função Inversa
Professor de Matemática Antonio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] HTTP://ensinodematemtica.blogspot.comhttp://accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com Dado um conjunto...
- Função Inversa
O objetivo de uma função inversa é criar funções a partir de outras. Uma função somente será inversa se for bijetora, isto é, os pares ordenados da função f deverão pertencer à função inversa f –1 da seguinte maneira: (x,y) Є f –1...
- Relação E Função
Se em uma relação de dois conjuntos A e B, todos os elementos x de A estiver relacionados com um elemento y de B, dizemos que essa relação é uma função bijetora. Toda função bijetora tem a sua forma inversa. Veja um exemplo de função bijetora...
- Função Inversa
O objetivo de uma função inversa é criar funções a partir de outras. Uma função somente será inversa se for bijetora, isto é, os pares ordenados da função f deverão pertencer à função inversa f –1 da seguinte maneira: (x,y) Є f –1...
- Função Composta E Inversa
Função Composta Observando as funções f : x →y | y = x + 1 e g : y →z | z = y2, representadas por diagramas de setas, notamos que, em f, x leva a y e, em g, y leva a z: Mas há uma função que permite “ir direto” de X para Z, sem passar...
Matemática
Funções, Inversa e Composta
Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email [email protected]
www.ensinodematemtica.blogspot.com.br
www.accbarrosogestar.blogspot.com.br
www.accbarrosogestar.wordpress.com
1 - FUNÇÃO INVERSA
Dada uma função f : A ® B , se f é bijetora , então define-se a função inversa f -1 como sendo a função de B em A , tal que f -1 (y) = x .
Veja a representação a seguir:

É óbvio então que:
a) para obter a função inversa , basta permutar as variáveis x e y .
b) o domínio de f -1 é igual ao conjunto imagem de f .
c) o conjunto imagem de f -1 é igual ao domínio de f .
d) os gráficos de f e de f -1 são curvas simétricas em relação à reta y = x ou seja , à bissetriz do primeiro quadrante .
Exemplo:Determine a INVERSA da função definida por y = 2x + 3.
Permutando as variáveis x e y, fica: x = 2y + 3
Explicitando y em função de x, vem:
2y = x - 3 \ y = (x - 3) / 2, que define a função inversa da função dada.
O gráfico abaixo, representa uma função e a sua inversa.
Observe que as curvas representativas de f e de f-1, são simétricas em relação à reta
y = x, bissetriz do primeiro e terceiro quadrantes.

Exercício resolvido:
A função f: R ® R , definida por f(x) = x2 :
a) é inversível e sua inversa é f -1 (x) = Ö x
b) é inversível e sua inversa é f -1(x) = - Ö x
c) não é inversível
d) é injetora
e) é bijetora
SOLUÇÃO:
Já sabemos que somente as funções bijetoras são inversíveis, ou seja, admitem função inversa. Ora, a função f(x) = x2, definida em R - conjunto dos números reais - não é injetora, pois elementos distintos possuem a mesma imagem. Por exemplo,
f(3) = f(-3) = 9. Somente por este motivo, a função não é bijetora e, em conseqüência, não é inversível.
Observe também que a função dada não é sobrejetora, pois o conjunto imagem da função f(x) = x2 é o conjunto R + dos números reais não negativos, o qual não coincide com o contradomínio dado que é
igual a R. A alternativa correta é a letra C.
2 - FUNÇÃO COMPOSTA
Chama-se função composta ( ou função de função ) à função obtida substituindo-se a variável independente x , por uma função.
Simbologia : fog (x) = f(g(x)) ou gof (x) = g(f(x)) .
Veja o esquema a seguir:

Obs : atente para o fato de que fog ¹ gof , ou seja, a operação " composição de funções " não é comutativa .
Exemplo:
Dadas as funções f(x) = 2x + 3 e g(x) = 5x, pede-se determinar gof(x) e fog(x).
Teremos:
gof(x) = g[f(x)] = g(2x + 3) = 5(2x + 3) = 10x + 15
fog(x) = f[g(x)] = f(5x) = 2(5x) + 3 = 10x + 3
Observe que fog ¹ gof .
Exercícios resolvidos:
1 - Sendo f e g duas funções tais que: f(x) = ax + b e g(x) = cx + d . Podemos afirmar que a igualdade gof(x) = fog(x) ocorrerá se e somente se:
a) b(1 - c) = d(1 - a)
b) a(1 - b) = d(1 - c)
c) ab = cd
d) ad = bc
e) a = bc
SOLUÇÃO:
Teremos:
fog(x) = f[g(x)] = f(cx + d) = a(cx + d) + b \ fog(x) = acx + ad + b
gof(x) = g[f(x)] = g(ax + b) = c(ax + b) + d \ gof(x) = cax + cb + d
Como o problema exige que gof = fog, fica:
acx + ad + b = cax + cb + d
Simplificando, vem:
ad + b = cb + d
ad - d = cb - b \ d(a - 1) = b(c - 1), que é equivalente a d(a - 1) = b(c - 1), o que nos leva a concluir que a alternativa correta é a letra A. .
2 - Sendo f e g duas funções tais que fog(x) = 2x + 1 e g(x) = 2 - x então f(x) é:
a) 2 - 2x
b) 3 - 3x
c) 2x - 5
*d) 5 - 2x
e) uma função par.
SOLUÇÃO:
Sendo fog(x) = 2x + 1, temos: f[g(x)] = 2x + 1
Substituindo g(x) pelo seu valor, fica: f(2 - x) = 2x + 1
Fazendo uma mudança de variável, podemos escrever 2 - x = u, sendo u a nova variável. Portanto, x = 2 - u.
Substituindo, fica:
f(u) = 2(2 - u) + 1 \ f(u) = 5 - 2u
Portanto, f(x) = 5 - 2x , o que nos leva à alternativa D.
Agora resolva esta:
Dadas as funções f(x) = 4x + 5 e g(x) = 2x - 5k, ocorrerá gof(x) = fog(x) se e somente se k for igual a:
*a) -1/3
b) 1/3
c) 0
d) 1
e) -1
- Função Inversa
Professor de Matemática Antonio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] HTTP://ensinodematemtica.blogspot.comhttp://accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com Dado um conjunto...
- Função Inversa
O objetivo de uma função inversa é criar funções a partir de outras. Uma função somente será inversa se for bijetora, isto é, os pares ordenados da função f deverão pertencer à função inversa f –1 da seguinte maneira: (x,y) Є f –1...
- Relação E Função
Se em uma relação de dois conjuntos A e B, todos os elementos x de A estiver relacionados com um elemento y de B, dizemos que essa relação é uma função bijetora. Toda função bijetora tem a sua forma inversa. Veja um exemplo de função bijetora...
- Função Inversa
O objetivo de uma função inversa é criar funções a partir de outras. Uma função somente será inversa se for bijetora, isto é, os pares ordenados da função f deverão pertencer à função inversa f –1 da seguinte maneira: (x,y) Є f –1...
- Função Composta E Inversa
Função Composta Observando as funções f : x →y | y = x + 1 e g : y →z | z = y2, representadas por diagramas de setas, notamos que, em f, x leva a y e, em g, y leva a z: Mas há uma função que permite “ir direto” de X para Z, sem passar...
