Matemática
OO’ é a distância entre o plano que contém o centro O' e o plano que contém o centro da esfera.
Qualquer plano que secciona uma esfera de raio R determina como seção plana um círculo de raio "R".
R2 = d2 + r2 ( teorema de pitágoras )
- Prisma
Prisma é um sólido geométrico delimitado por faces planas, no qual as bases se situam em planos paralelos. Quanto à inclinação das arestas laterais, os prismas podem ser retos ou oblíquos. Prisma reto As arestas laterais têm o mesmo comprimento....
- Volume Do Tronco De Pirâmide
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Cone
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
- Pirâmides
Dada uma região poligonal de n vértices e um ponto V fora da região (outro plano), ao traçarmos segmentos de retas entre os vértices da região poligonal e o ponto V, construímos uma pirâmide que será classificada de acordo com o número de lados...
- Volume Do Tronco De Pirâmide
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.br www.accbarrosogestar.wordpress.comwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...
Matemática
Geometria Espacial
A geometria espacial euclidiana pode ser estuda em dois aspectos:
geometria espacial de posição e geometria espacial métrica.
geometria espacial de posição e geometria espacial métrica.
Geometria espacial de posição
Os entes geométricos envolvidos na geometria espacial de posição são: o ponto, a reta e o plano.
Tais elementos geométricos são ideias primitivas e não se definem, apenas suas existências são aceitas.
Tais elementos geométricos são ideias primitivas e não se definem, apenas suas existências são aceitas.
Geralmente, eles são representados por letras.
os pontos e as retas com letras do alfabeto latino.
Os pontos com as maiúsculas ; A, B, C, etc.
As retas com as minúsculas: r, s, t, etc.
Já os planos com letras minúsculas do alfabeto grego: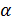
, 
, 
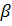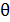, etc.
os pontos e as retas com letras do alfabeto latino.
Os pontos com as maiúsculas ; A, B, C, etc.
As retas com as minúsculas: r, s, t, etc.
Já os planos com letras minúsculas do alfabeto grego:
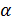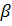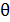, , , etc.O ponto não tem dimensão.
A reta tem uma única dimensão ( comprimento ).
O plano tem duas dimensões ( comprimento e largura ).
A reta tem uma única dimensão ( comprimento ).
O plano tem duas dimensões ( comprimento e largura ).
Posições relativas entre ponto e reta
Alguns axiomas ( verdades válidas e inquestionáveis sem a necessidade de demonstração ) sobre ponto e reta:
1) Existe infinitos pontos em uma reta e, também, fora dela.
2) Por dois pontos distintos passam uma única reta.
3) Três pontos colineares ( mesma linha ) estão em uma única reta.
4) Um ponto em uma reta divide-a em duas semirretas que o contém.
5) A parte que está entre dois pontos distintos de uma reta, incluindo eles, é dito segmento de reta.
Em relação a um reta, um ponto pode pertencer a uma reta ou não.
1) Existe infinitos pontos em uma reta e, também, fora dela.
2) Por dois pontos distintos passam uma única reta.
3) Três pontos colineares ( mesma linha ) estão em uma única reta.
4) Um ponto em uma reta divide-a em duas semirretas que o contém.
5) A parte que está entre dois pontos distintos de uma reta, incluindo eles, é dito segmento de reta.
Em relação a um reta, um ponto pode pertencer a uma reta ou não.
Posições relativas entre ponto e plano
Alguns postulados ( ou axiomas ) sobre ponto e plano:
1) Em um plano, bem como fora dele, existe infinitos pontos.
2) Três pontos não colineares determinam um único plano que os contém.
3) Se dois pontos distintos estão em um plano, a reta que passa por eles também está.
Em relação a um plano, um ponto pode pertencer a um plano ou não.
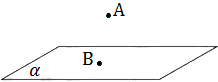
1) Em um plano, bem como fora dele, existe infinitos pontos.
2) Três pontos não colineares determinam um único plano que os contém.
3) Se dois pontos distintos estão em um plano, a reta que passa por eles também está.
Em relação a um plano, um ponto pode pertencer a um plano ou não.
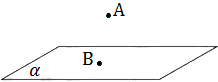
Posições relativas entre duas retas
Duas retas podem ser:
paralelas, concorrentes ou reversas.
As paralelas, que são coplanares ( mesmo plano ), podem ser:
paralelas coincidentes ( tem todos os pontos em comum )
paralelas distintas ( sem ponto em comum ).
As concorrentes, que são coplanares, têm apenas um ponto em comum.
As concorrentes podem ser perpendiculares se formarem entre si um ângulo reto.
As reversas, que não são coplanares, não têm pontos em comum.
As reversas podem ser ortogornais se existir uma paralela a uma delas que seja perpendicular a outra.
paralelas, concorrentes ou reversas.
As paralelas, que são coplanares ( mesmo plano ), podem ser:
paralelas coincidentes ( tem todos os pontos em comum )
paralelas distintas ( sem ponto em comum ).
As concorrentes, que são coplanares, têm apenas um ponto em comum.
As concorrentes podem ser perpendiculares se formarem entre si um ângulo reto.
As reversas, que não são coplanares, não têm pontos em comum.
As reversas podem ser ortogornais se existir uma paralela a uma delas que seja perpendicular a outra.
Posições relativas entre reta e plano
Alguns postulados sobre reta e plano:
1) Duas retas concorrentes determinam um único plano.
2) Duas retas paralelas distintas determinam um único plano.
3) Uma reta e um ponto fora dela determinam um único plano.
Em relação a um plano, uma reta pode:
está contida, ser paralela ou ser concorrente.
Está contida se pelo menos dois pontos da reta estiverem no plano.
São concorrentes se a reta e o plano tiverem um ponto em comum.
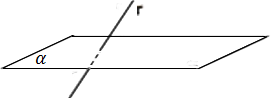
Paralelas se a reta e o plano não tiverem ponto em comum.
1) Duas retas concorrentes determinam um único plano.
2) Duas retas paralelas distintas determinam um único plano.
3) Uma reta e um ponto fora dela determinam um único plano.
Em relação a um plano, uma reta pode:
está contida, ser paralela ou ser concorrente.
Está contida se pelo menos dois pontos da reta estiverem no plano.
São concorrentes se a reta e o plano tiverem um ponto em comum.
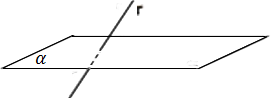
Paralelas se a reta e o plano não tiverem ponto em comum.
Posições relativas entre dois planos
Dois planos podem ser:
coincidentes, paralelos ou concorrentes ( secantes ).
Coincidentes se todos os pontos de um são também do outro.
Paralelos se não houver ponto em comum aos dois planos.
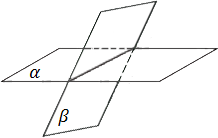
Secantes se tiverem uma reta em comum ( se interceptem ).
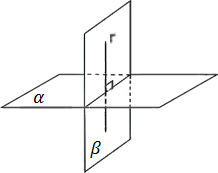
Perpendiculares se existe uma reta em um deles que é perpendicular a reta comum aos planos.
coincidentes, paralelos ou concorrentes ( secantes ).
Coincidentes se todos os pontos de um são também do outro.
Paralelos se não houver ponto em comum aos dois planos.
Secantes se tiverem uma reta em comum ( se interceptem ).
Perpendiculares se existe uma reta em um deles que é perpendicular a reta comum aos planos.
Projeção ortogonal
A projeção ortogonal de um ponto num plano é um ponto, projetado com o auxílio de uma reta perpendicular ao plano.
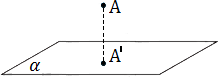
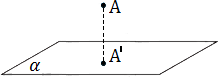
A projeção de uma reta sobre um plano pode ser uma reta ou um ponto.
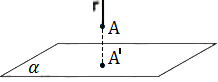
Geometria espacial métrica
Prismas
Prisma é um sólido geométrico delimitado por duas bases poligonais paralelas.
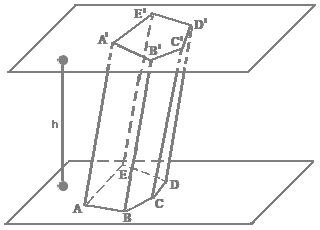
Os polígonos ABCDE e A'B'C'D'E' são as bases do prisma.
Os polígonos ABB'A', BCC'B', CDD'C', DEE'D', AEE'A' são as faces laterais.
Os segmentos AB, BC, CD, DE, AE, A'B', B'C', C'D', D'E', A'E' são as arestas da base.
AA', BB', CC', DD', EE' são as arestas laterais.
A distância entre as bases, h, é a altura do prisma.
Os polígonos ABCDE e A'B'C'D'E' são as bases do prisma.
Os polígonos ABB'A', BCC'B', CDD'C', DEE'D', AEE'A' são as faces laterais.
Os segmentos AB, BC, CD, DE, AE, A'B', B'C', C'D', D'E', A'E' são as arestas da base.
AA', BB', CC', DD', EE' são as arestas laterais.
A distância entre as bases, h, é a altura do prisma.
Nomeclatura
Os primas recebem nomes de acordo com o polígono de suas bases.
Se as bases são triangulares então o prisma é chamado de prisma triangular.
Assim, tem-se:
Prismas triangulares, prismas quadrangulares, prismas pentagonais, prismas hexagonais, etc.
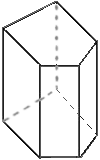
Se as bases são triangulares então o prisma é chamado de prisma triangular.
Assim, tem-se:
Prismas triangulares, prismas quadrangulares, prismas pentagonais, prismas hexagonais, etc.
Classificação
Os prismas são classificados de acordo com a inclinação das arestas laterais:
Se as arestas laterais são inclinadas em relação as bases, o prisma é oblíquo.
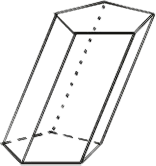
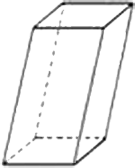
Se as arestas leterais são perpendiculares em relação as bases, o prisma é reto.
Um prisma reto cujas bases são polígonos regulares ( arestas das bases de mesmo tamanho ) é chamado de prisma regular.
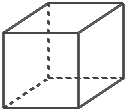
Se as arestas laterais são inclinadas em relação as bases, o prisma é oblíquo.
Se as arestas leterais são perpendiculares em relação as bases, o prisma é reto.
Um prisma reto cujas bases são polígonos regulares ( arestas das bases de mesmo tamanho ) é chamado de prisma regular.
Cálculo de áreas de polígonos
Triângulos:
A área de um triângulo é dada por:
Striângulo = b . h ( conhecendo-se a base e a altura do triângulo )
ou pela fórmula de Heron:
Conhecendo-se os lados "a", "b" e "c" e o semi-perímetro p = (a + b + c) / 2
Striângulo =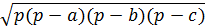
A área do triângulo equilátero de lado "a":
Striângulo equilátero =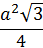
Quadriláteros:
A área do paralelogramo:
S = b . h
A área do retângulo:
S = b . h
A área do quadrado de lado "a":
S = a2
A área do losango:
Considerando "D" a diagonal maior e "d" a diagonal menor:
S = ( D . d ) / 2
A área do trapézio:
Considerando "B" a base maior, "b" a base menor e "h" a altura do trapézio:
S = [ (B + b) . h ] / 2
Pentágono regular:
Spentágono =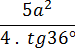
Hexágono regular:
Shexágono =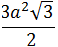
A área de um triângulo é dada por:
Striângulo = b . h ( conhecendo-se a base e a altura do triângulo )
ou pela fórmula de Heron:
Conhecendo-se os lados "a", "b" e "c" e o semi-perímetro p = (a + b + c) / 2
Striângulo =
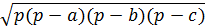
A área do triângulo equilátero de lado "a":
Striângulo equilátero =
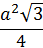
Quadriláteros:
A área do paralelogramo:
S = b . h
A área do retângulo:
S = b . h
A área do quadrado de lado "a":
S = a2
A área do losango:
Considerando "D" a diagonal maior e "d" a diagonal menor:
S = ( D . d ) / 2
A área do trapézio:
Considerando "B" a base maior, "b" a base menor e "h" a altura do trapézio:
S = [ (B + b) . h ] / 2
Pentágono regular:
Spentágono =
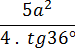
Hexágono regular:
Shexágono =
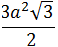
Cálculo da área de um prisma
As bases são sempre congruentes então a medida da área de uma base é igual a da outra base.
A área totaldo prisma é igual a área das bases mais a área lateral ( de todas as faces ).
Sprisma = 2 . SB + SL
Se a base for um polígono regular então:
as faces laterais serão congruentes, então a medida da área de uma face é igual a de qualquer uma face.
Sprisma = 2 . SB + SL
Se a base for um polígono regular então:
as faces laterais serão congruentes, então a medida da área de uma face é igual a de qualquer uma face.
Cálculo do volume de um prisma
O volume de um prisma é igual a área da base vezes a altura do prisma.
Vprisma = SB . h
Vprisma = SB . h
Exemplo:
Um prisma triangular reto regular de aresta da base 4 cm e altura 5 cm, tem área e volume dados por:
planificação de um prisma triangular:
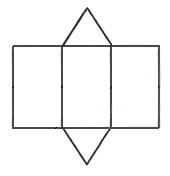
A área da base ( que é um triângulo equilátero ) é dada por:
SB =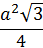
SB = 42/4 .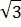
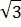= 4 cm2
A área lateral ( que são 3 retângulos ) é dada por:
SL = 3 . a . h = 3 . 4 . 5 = 60 cm2
ST = 2 . SB + SL
ST = 2 . 4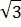 + 60 = 8 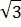+ 60 cm2
O volume é dado por:
V = SB . h
V = 4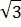 . 5 = 20 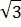cm2
Um prisma triangular reto regular de aresta da base 4 cm e altura 5 cm, tem área e volume dados por:
planificação de um prisma triangular:
A área da base ( que é um triângulo equilátero ) é dada por:
SB =
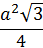
SB = 42/4 .
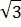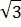= 4 cm2A área lateral ( que são 3 retângulos ) é dada por:
SL = 3 . a . h = 3 . 4 . 5 = 60 cm2
ST = 2 . SB + SL
ST = 2 . 4
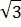+ 60 = 8 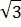+ 60 cm2O volume é dado por:
V = SB . h
V = 4
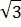. 5 = 20 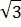cm2Prismas quadrangulares especiais
Paralelepípedo:
Prisma quadrangular cujas bases são paralelogramos.
Num paralelepípedo reto regular de arestas da base "a" e "b" e altura "h", a área é dada por:
SB = a . b
SL = 2 . a . h + 2 . b . h
ST = 2 . a . b + 2 . a . h + 2 . b . h = 2 . (a . b + a . h + b . h)
A diagonal da base é dada por:
dB =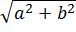
A diagonal do paralelepípedo é dada por:
Dparalelepípedo =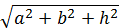
O volume é dado por:
Vparalelepípedo = a . b . h
Prisma quadrangular cujas bases são paralelogramos.
Num paralelepípedo reto regular de arestas da base "a" e "b" e altura "h", a área é dada por:
SB = a . b
SL = 2 . a . h + 2 . b . h
ST = 2 . a . b + 2 . a . h + 2 . b . h = 2 . (a . b + a . h + b . h)
A diagonal da base é dada por:
dB =
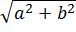
A diagonal do paralelepípedo é dada por:
Dparalelepípedo =
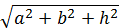
O volume é dado por:
Vparalelepípedo = a . b . h
Cubo:
Prisma quadrangular reto regular cujas seis faces são quadrados congruentes.
A área do cubo é seis vezes a área da base.
Considerando "a" como medida das arestas tem-se:
SB = a . a = a2
Scubo = 6 . a2
A diagonal do cubo é dada por:
dcubo = a .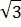
O volume do cubo é dado por:
Vcubo = a . a . a = a3
Prisma quadrangular reto regular cujas seis faces são quadrados congruentes.
A área do cubo é seis vezes a área da base.
Considerando "a" como medida das arestas tem-se:
SB = a . a = a2
Scubo = 6 . a2
A diagonal do cubo é dada por:
dcubo = a .
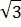
O volume do cubo é dado por:
Vcubo = a . a . a = a3
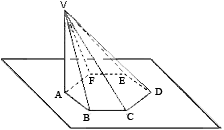
Pirâmides
É o sólido geométrico formado por todas as projeções ( ortogonais e não ortogonais ) de um ponto em uma superfície poligonal.
O polígono ABCDEF é a base da pirâmide.
O ponto V é o vértice da pirâmide.
Os triângulos ABV, BCV, CDV, DEV, EFV, FAV são as faces laterais.
Os segmentos AB, BC, CD, DE, EF, FA são as arestas da base.
Os segmentos AV, BV, CV, DV, EV, FV são as arestas laterais.
A projeção ortogonal de V no plano que contem a base é a altura, h, da pirâmide.
As alturas das faces laterais são chamadas de apótema da pirâmide.
O ponto V é o vértice da pirâmide.
Os triângulos ABV, BCV, CDV, DEV, EFV, FAV são as faces laterais.
Os segmentos AB, BC, CD, DE, EF, FA são as arestas da base.
Os segmentos AV, BV, CV, DV, EV, FV são as arestas laterais.
A projeção ortogonal de V no plano que contem a base é a altura, h, da pirâmide.
As alturas das faces laterais são chamadas de apótema da pirâmide.
Nomeclatura
A pirâmide recebe o nome de acordo com o polígono da base.
Assim tem-se:
Pirâmide triângular, pirâmide quadrangular, pirâmide pentagonal, etc.
As pirâmides triângulares são chamadas de tetraedro.
Assim tem-se:
Pirâmide triângular, pirâmide quadrangular, pirâmide pentagonal, etc.
As pirâmides triângulares são chamadas de tetraedro.
Classificação
Quando a projeção do vértice coincide com o centro da base a pirâmide é dita reta, caso contrário é dita oblíqua.
Uma pirâmide é dita regular quando é reta e a base é um polígono regular.
Uma pirâmide é dita regular quando é reta e a base é um polígono regular.
Cálculo da área de uma pirâmide
A área de uma pirâmide é dada pela área da base mais a área lateral:
Spirâmide = SB + SL
Se a pirâmide for regular as faces laterais serão triângulos isósceles congruentes.
Spirâmide = SB + SL
Se a pirâmide for regular as faces laterais serão triângulos isósceles congruentes.
Cálculo do volume de uma pirâmide
O volume de uma pirâmide é dado por um terço da áea da base vezes a altura:
Vpirâmide =
. SB . h
Vpirâmide =
. SB . hTronco de pirâmide
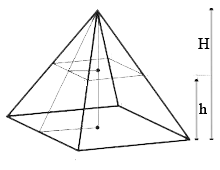
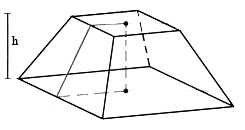
Uma secção paralela a base de uma pirâmide divide-a em uma pirâmide menor e em um tronco de pirâmide.
Se o tronco de pirâmide for regular:
as bases são polígonos regulares paralelos e semelhantes
as faces laterais são trapézios isósceles congruentes
a altura de qualquer face lateral é o apótema do tronco.
Se o tronco de pirâmide for regular:
as bases são polígonos regulares paralelos e semelhantes
as faces laterais são trapézios isósceles congruentes
a altura de qualquer face lateral é o apótema do tronco.
Cálculo da área do tronco de pirâmide
A área será formada pelas áreas da base maior, da base menor e a área lateral do tronco:
Stronco da pirâmide = SB + Sb + SLtronco
Considerando "aB" a aresta da base maior, "ab" a aresta da base menor, "H" a altura da pirâmide, "h" a altura do tronco, tem-se:
aB / ab = H / (H – h)
aB2 / ab2 = H2 / (H – h)2
aB3 / ab3 = H3 / (H – h)3
Stronco da pirâmide = SB + Sb + SLtronco
Considerando "aB" a aresta da base maior, "ab" a aresta da base menor, "H" a altura da pirâmide, "h" a altura do tronco, tem-se:
aB / ab = H / (H – h)
aB2 / ab2 = H2 / (H – h)2
aB3 / ab3 = H3 / (H – h)3
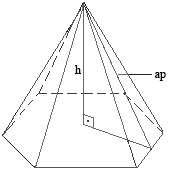
Cálculo do volume do tronco de pirâmide
O volume do tronco da pirâmide pode ser calculado pela diferença dos volumes das pirâmides ( a maior e a que é retirada para formar o tronco ).
Vtronco = ( SB. H – Sb . (H – h) )
ou por:
Vtronco pirâmide =
. ( SB + Sb +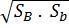 
)
Vtronco =
( SB. H – Sb . (H – h) )ou por:
Vtronco pirâmide =
. ( SB + Sb + 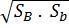)Cilindros
É um sólido geométrico determinado pela projeção de todos os pontos de um círculo contido em um plano em outro plano paralelo.
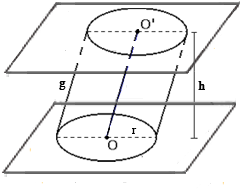
A projeção de qualquer ponto do plano é chamada de geratriz do cilindro, a distâcia entre os planos é a altura do cilindro.
Classificação
Se a geratriz for perpendicular as bases o cilindro é dito reto, caso contrário, é dito oblíquo.
Chama-se secção meridiana de um cilindro a intersecção do cilindro com um plano que contém seu eixo.
Um cilindro reto em que a altura é igual ao diâmetro da base é dito cilindro equilátero.
Chama-se secção meridiana de um cilindro a intersecção do cilindro com um plano que contém seu eixo.
Um cilindro reto em que a altura é igual ao diâmetro da base é dito cilindro equilátero.
Cálculo da área de um cilindro
A área de um cilindro é dada pelas áreas das duas bases mais a área lateral.
Scilindro = 2 . SB + SL
Scilindro = 2 . SB + SL
Em um cilindro reto a área é dada por:
SB =
. R2
SL = 2 . . R . h
Scilindro = 2 . . R2 + 2 . . R . h = 2 . . R . (R + h)
SB =
. R2SL = 2 .
. R . hScilindro = 2 .
. R2 + 2 . . R . h = 2 . . R . (R + h)Cálculo do volume de um cilindro
O volume do cilindro é dado pela área da base vezes a geratriz:
Vcilindro = SB . g
No cilindro reto é dado por:
Vcilindro = . R2 . h
Vcilindro = SB . g
No cilindro reto é dado por:
Vcilindro =
. R2 . hCones
É o sólido geométrico formado por todas as projeções ( ortogonais e não ortogonais ) de um ponto em uma superfície circular.
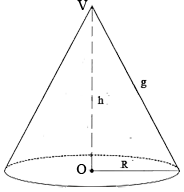
O vértice do cone é o ponto V.
A geratriz "g" do cone é uma reta que passa no vértice e em qualquer ponto da circunferência da base.
A altura "h" é a projeção ortogonal do vértice.
A geratriz "g" do cone é uma reta que passa no vértice e em qualquer ponto da circunferência da base.
A altura "h" é a projeção ortogonal do vértice.
Classificação
Se o eixo OV for perpendicular a base o cone é dito reto, caso contrário, é oblíquo.
Chama-se secção meridiana do cone a interseção do cone com um plano que contém seu eixo.
Todo cone em que a geratriz é igual ao diâmetro da base é dito cone equilátero.
Chama-se secção meridiana do cone a interseção do cone com um plano que contém seu eixo.
Todo cone em que a geratriz é igual ao diâmetro da base é dito cone equilátero.
Cálculo da área de um cone
A área do cone é dada pela área da base mais a área lateral.
Scone = SB + SL
Se o cone é reto então a área é dada por:
Scone = . R2 + . R . g = = . R . (R + g)
Scone = SB + SL
Se o cone é reto então a área é dada por:
Scone =
. R2 + . R . g = = . R . (R + g)Cálculo do volume de um cone
O volume de um cone é um terço da área da base vezes a altura. Vcone = . SB . h
Vcone = . . R2 . h
. SB . hVcone =
. . R2 . hTronco do cone
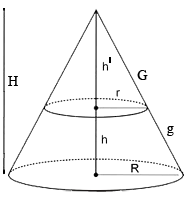
Uma secção paralela a base de um cone divide-o em um outro cone menor e em um tronco de cone.
As bases são paralelas
A altura do tronco "h" é a distância entre os planos das bases.
O raio da base maior é "R".
O raio da base menor é "r".
A geratriz do tronco do cone é "g".
Assim, tem-se:
R / r = H / (H – h) = G / g
R2 + H2 = G2
(R – r)2 + h2 = g2
As bases são paralelas
A altura do tronco "h" é a distância entre os planos das bases.
O raio da base maior é "R".
O raio da base menor é "r".
A geratriz do tronco do cone é "g".
Assim, tem-se:
R / r = H / (H – h) = G / g
R2 + H2 = G2
(R – r)2 + h2 = g2
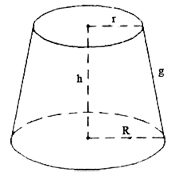
Cálculo da área do tronco de um cone
A área do tronco do cone é dada pelas áreas das bases maior e menor e pela área lateral.
Stronco de cone = SB + Sb + SL
Stronco de cone = . R2 + . r2 + . (R + r) . g = . [(R + r) . g + R2 + r2]
Stronco de cone = SB + Sb + SL
Stronco de cone =
. R2 + . r2 + . (R + r) . g = . [(R + r) . g + R2 + r2]Cálculo do volume do tronco de um cone
O volume do tronco de um cone é dado por:
Vtronco de cone = . . [ R2 + R . r + r2 ]
Vtronco de cone =
. . [ R2 + R . r + r2 ]Esferas
A superfície esférica de centro "O" é o conjunto de pontos do espaço cuja distância ao centro é igual ao raio "R".
A esfera de centro "O" para ser considerada sólido geométrico deve conter também os pontos interiores a superfície esférica.
A distância OP é igual ao raio da esfera "R".
A esfera de centro "O" para ser considerada sólido geométrico deve conter também os pontos interiores a superfície esférica.
A distância OP é igual ao raio da esfera "R".
Cálculo da área da esfera
A área da superfície esférica é dada por:
Sesfera = 4 . . R2
Sesfera = 4 .
. R2Cálculo do volume da esfera
O volume da esfera é dado por:
Vesfera = (4/3) . . R3
Vesfera = (4/3) .
. R3Secção de uma esfera
OO’ é a distância entre o plano que contém o centro O' e o plano que contém o centro da esfera.
Qualquer plano que secciona uma esfera de raio R determina como seção plana um círculo de raio "R".
R2 = d2 + r2 ( teorema de pitágoras )
Exercícios Resolvidos
R01 — Qual o volume de um prisma triangular com todas as arestas congruentes de área 12 cm2?
A área lateral é formada por 3 quadrados de aresta "a", então tem-se:
3 . a2 = 12
a2 = 4
a = 2
A base é um triângulo equilátero de aresta "a" (a = 2), logo a área da base é dada por:
SB = (22/4) .
SB =
Logo, o volume é dado pela área da base vezes a altura (a = 2):
Vprisma = 2 .
3 . a2 = 12
a2 = 4
a = 2
A base é um triângulo equilátero de aresta "a" (a = 2), logo a área da base é dada por:
SB = (22/4) .
SB =
Logo, o volume é dado pela área da base vezes a altura (a = 2):
Vprisma = 2 .
R02 — A base de uma prisma reto de 5 cm de altura é um quadrado de aresta 2 cm. Qual a sua área?
A área da base é 22 = 4 cm2
Cada face é um retangulo 5 po 2, logo tem área 5 . 2 = 10 cm2
Sprisma = 2 . S2 . h
Sprisma = 2 . 4 . 5 = 40 cm2.
Cada face é um retangulo 5 po 2, logo tem área 5 . 2 = 10 cm2
Sprisma = 2 . S2 . h
Sprisma = 2 . 4 . 5 = 40 cm2.
R03 — Um paralelepípedo reto retângulo tem arestas 2, 3 e 4 cm. Qual a medida da sua diagonal?
A diagonal é dada por D =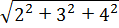 
= 
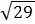
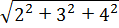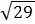
= R04 — Determine a área e o volume de um prisma hexagonal regular de altura 4 cm e aresta da base 2 cm.
Como a base é um hexágono regular então a área é dada por:
SB = 3 . 22 /2 . = 6
A área lateral é formada por seis retângulos 4 por 2, logo SL = 6 . 4 . 2 = 48
ST = 2 . 6 . + 48 = 12 + 48
O volume é dado pela área da base vezes a altura, assim:
V = 6 . . 4 = 24
SB = 3 . 22 /2 .
= 6 A área lateral é formada por seis retângulos 4 por 2, logo SL = 6 . 4 . 2 = 48
ST = 2 . 6 .
+ 48 = 12 + 48O volume é dado pela área da base vezes a altura, assim:
V = 6 .
. 4 = 24 R05 — Um cubo tem área 24 cm2. Quanto vale a diagonal desse cubo?
A área do cubo é 6 vezes a aresta ao quadrado, assim:
6 . a2 = 24
a2 = 4
a = 2
A diagonal do cubo é dada por: D = a .
D = 2
6 . a2 = 24
a2 = 4
a = 2
A diagonal do cubo é dada por: D = a .
D = 2
R06 — Numa pirâmide quadrangular, a aresta mede 10 cm e a altura é 12 cm. Calcule a área total e o volume dessa pirâmide.
A área da base que é um quadrado é:
SB = 102 = 100 cm2
A área lateral que são quatro triângulos isósceles é dada por:
SL = 4 . 10 . h ( apótema )
h2 = 122 + (10/2)2
h2 = 144 + 25 = 169
h = 13
SL = 4 . 10 . 13 = 520 cm2
ST = 2 . 100 + 520 = 720 cm2
O volume é dado por área da base vezes altura
V = 100 . 12 = 1200 cm3
SB = 102 = 100 cm2
A área lateral que são quatro triângulos isósceles é dada por:
SL = 4 . 10 . h ( apótema )
h2 = 122 + (10/2)2
h2 = 144 + 25 = 169
h = 13
SL = 4 . 10 . 13 = 520 cm2
ST = 2 . 100 + 520 = 720 cm2
O volume é dado por área da base vezes altura
V = 100 . 12 = 1200 cm3
R07 — Qual o volume de um tronco de pirâmide quadrangular regular, se os lados das bases medem 6 cm e 4 cm e a altura do tronco mede 12 cm?
Calculando as áreas das bases tem-se:
SB = 62 = 36 cm2 e Sb = 42 = 16 cm2
V = h/3 . (SB +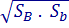
+ Sb)
V = 12/3 . (36 +
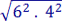+ 16)
V = 12/3 . (36 + 24 + 16) = 4 . 76 = 304 cm3
SB = 62 = 36 cm2 e Sb = 42 = 16 cm2
V = h/3 . (SB +
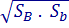+ Sb)V = 12/3 . (36 +
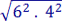+ 16)V = 12/3 . (36 + 24 + 16) = 4 . 76 = 304 cm3
R08 — Qual a área e o volume de um cilindro reto cuja diagonal da base vale 6 cm e altura 8 cm?
Como a diagonal da base e 6, então o raio R é 3 cm.
A área da base é dada por:
SB =
. R2
SB = . 32 = 9
A área lateral é dada por:
SL = 2 . . R . h = 2 . . 3 . 8 = 48
A área total é dada por:
ST = 2 . 9 + 48 = 66 cm2
O volume é dado por:
V = . R2 . h = . 9 . 8 = 72 cm3
A área da base é dada por:
SB =
. R2SB =
. 32 = 9 A área lateral é dada por:
SL = 2 .
. R . h = 2 . . 3 . 8 = 48 A área total é dada por:
ST = 2 . 9
+ 48 = 66 cm2O volume é dado por:
V =
. R2 . h = . 9 . 8 = 72 cm3R09 — Um cone reto tem diâmetro igual a 6 cm e altura igual a 15 cm. Se diminuir o diâmetro para 4 cm, mantendo a mesma altura. Determine os dois volumes e diga em quantos por cento varia o volume?
Se o diâmetro é 6 então o raio é 3, assim:
SB1 = . 32 = 9
V1 = (1/3) . SB . h = (1/3) . 9 . 15 = 45 cm3
Com diâmetro 4 o raio é 2, assim:
SB2 = . 22 = 4
V2 = (1/3) . SB . h = (1/3) . 4 . 15 = 20 cm3
V2 / V1 = (1/3) . SB2 . h = (1/3) . SB1 . h = 20 / 45 = 4/9
Assim, o volume do 2°
44,44% menor que o volume do 1°.
SB1 =
. 32 = 9 V1 = (1/3) . SB . h = (1/3) . 9
. 15 = 45 cm3Com diâmetro 4 o raio é 2, assim:
SB2 =
. 22 = 4 V2 = (1/3) . SB . h = (1/3) . 4
. 15 = 20 cm3V2 / V1 = (1/3) . SB2 . h = (1/3) . SB1 . h = 20 / 45 = 4/9
Assim, o volume do 2°
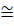44,44% menor que o volume do 1°.R10 — Um cone reto de 12 cm de altura e raio da base 6 cm é seccionado a 4 cm do vértice. Obtenha a área e o volume do tronco de cone formado por essa secção.
A altura do tronco do cone "h" é dada pela diferença entre a altura "H" do cone maior e a altura "h'" do cone menor:
h = H - h' = 12 – 4 = 8 cm
O raio da base menor pode se encontrado por:
r / R = h' / H
r / 6 = 4 / 12
r = 24/12 = 2 cm
A geratriz "g" do tronco de cone pode ser encontrada por:
(R – r)2 + h2 = g2
(6 – 2)2 + 82 = g2
42 + 64 = g2
16 + 64 = g2
80 = g2
g = 4 .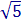
A área do tronco é dada por:
Stronco = . [(R + r) . g + R2 + r2]
Stronco = . [(6 + 2) . 4 . 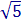+ 62 + 22]
Stronco = . [ 8 . 4 . 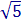+ 36 + 4 ]
Stronco = . [ 32 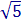+ 40 ] cm2
V = (h / 3) . . [R2 + R . r + r2]
V = (8/3) . . [62 + 6 . 2 + 22]
V = (8/3) . . [36 + 12 + 4]
V = (8 . 52)/3 .
V = (416/3) cm3
h = H - h' = 12 – 4 = 8 cm
O raio da base menor pode se encontrado por:
r / R = h' / H
r / 6 = 4 / 12
r = 24/12 = 2 cm
A geratriz "g" do tronco de cone pode ser encontrada por:
(R – r)2 + h2 = g2
(6 – 2)2 + 82 = g2
42 + 64 = g2
16 + 64 = g2
80 = g2
g = 4 .
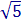
A área do tronco é dada por:
Stronco =
. [(R + r) . g + R2 + r2]Stronco =
. [(6 + 2) . 4 . 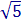+ 62 + 22]Stronco =
. [ 8 . 4 . 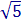+ 36 + 4 ]Stronco =
. [ 32 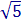+ 40 ] cm2V = (h / 3) .
. [R2 + R . r + r2]V = (8/3) .
. [62 + 6 . 2 + 22]V = (8/3) .
. [36 + 12 + 4]V = (8 . 52)/3 .
V = (416/3)
cm3R11 — Qual a área e o volume de uma esfera inscrita em um cubo de aresta 6 cm?
Se a esfera está inscrita no cubo então o raio da esfera é igual a metade da aresta do cubo.
R = 6/2 = 3 cm
A área da esfera é dada por:
S = 4 . R2
S = 4 . 32
S = 36 cm2
O volume da esfera é dado por:
V = (4/3) . R3
V = (4/3) . 33
V = (4 . 27/3)
V = 36 cm3
R = 6/2 = 3 cm
A área da esfera é dada por:
S = 4
. R2S = 4
. 32S = 36
cm2O volume da esfera é dado por:
V = (4/3)
. R3V = (4/3)
. 33V = (4 . 27/3)
V = 36
cm3Exercícios Propostos
P01 — Quanto vale a aresta de um tetraedro regular de volume 64 .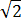 
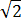cm3?
cm3?P02 — Qual o volume de um prisma retangular de arestas da base, 3 e 6 cm e altura 10 cm?
P04 — (SJRP - JUNDIAI) Os vértices de um tetraedro regular de volume 1 m3 são centros das faces de outro tetraedro regular. O volume deste outro tetraedro vale em cm3:
a) 1 b) 3 c) 9 d) 27 e) 81
a) 1 b) 3 c) 9 d) 27 e) 81
P05 — (OSEC) Um prisma e uma pirâmide tem bases com a mesma área. Se o volume do prisma é o dobro do volume da pirâmide, a altura da pirâmide será:
a) O triplo da do prisma.
b) O dobro da do prisma.
c) O triplo da metade da do prisma.
d) O dobro da terça parte da do prisma.
e) n.d.a
a) O triplo da do prisma.
b) O dobro da do prisma.
c) O triplo da metade da do prisma.
d) O dobro da terça parte da do prisma.
e) n.d.a
P06 — Qual a área e o volume de um prisma pentagonal regular de aresta da base 4 cm e altura 6 cm?
P07 — Secciona-se uma pirâmide regular de altura 2 cm por um plano paralelo à base, a uma distância de x do vértice. Determine x de modo que a áreas laterais da pirâmide se altura x e do tronco de pirâmide de altura 2 – x sejam iguais.
P08 — Calcular a área lateral de uma pirâmide quadrangular regular que tem 12 cm de altura e 40 cm de perímetro da base.
P09 — Se o apótema de uma pirâmide mede 17 m e o apótema da base mede 8 m, qual é a altura da pirâmide?
P10 — Qual é a área total de uma pirâmide quadrangular regular, sabendo-se que sua altura mede 12 cm e que o apótema da pirâmide mede 24 cm?
P11 — Um tronco de pirâmide de bases quadradas tem 700 cm3 de volume. A altura do tronco mede 12 cm e o lado do quadrado da base maior, 10 cm. Então, quanto vale o lado do quadrado da base menor?
P12 — (OSEC) Um prisma e uma pirâmide tem bases com a mesma área. Se o volume do prisma é o dobro do volume da pirâmide, a altura da pirâmide será:
a) O triplo da do prisma.
b) O dobro da do prisma.
c) O triplo da metade da do prisma.
d) O dobro da terça parte da do prisma.
e) n.d.a
a) O triplo da do prisma.
b) O dobro da do prisma.
c) O triplo da metade da do prisma.
d) O dobro da terça parte da do prisma.
e) n.d.a
P13 — Calcule a área de um cilindro reto cuja diâmetro da base é igual a altura e vale 6 cm.
P14 — Um líquido que está em um recipiente em forma de cone reto é despejado em outro de forma de um cilindro reto. Se ambos tem raio da base 10 cm e altura 20 cm, que altura atingirá o líquido no cilindro?
P15 — As áreas das bases de um cone circular reto e de um prisma quadrangular reto são iguais. O prisma tem altura 12 cm e volume igual ao dobro do volume do cone. Determinar a altura do cone.
P16 — Um cone circular reto tem 12 cm de altura e 16 cm de geratriz. Calcule a área e o volume desse cone.
P17 — A área lateral de um cone circular reto é de 15 m2 e a área total é de 24 m2. Calcule a medida do raio do cone.
P18 — Determinar a área lateral de um cone sendo 3 cm sua altura e 5 cm a soma da medida da geratriz com o raio da base.
P19 — Uma secção feita numa esfera por um plano é um círculo de perímetro 2π cm. A distância do centro da esfera ao plano é 2 raiz de 2 cm. Calcule a medida do raio da esfera.
P20 — O volume de uma esfera A é 1/8 do volume de uma esfera B. Se o raio da esfera B mede 10, então quanto mede o raio da esfera A?
P21 — Uma pirâmide quadrada tem todas as arestas medindo 2 cm. Então qual é o seu volume?
fonte:hpdemat.apphb.com
- Prisma
Prisma é um sólido geométrico delimitado por faces planas, no qual as bases se situam em planos paralelos. Quanto à inclinação das arestas laterais, os prismas podem ser retos ou oblíquos. Prisma reto As arestas laterais têm o mesmo comprimento....
- Volume Do Tronco De Pirâmide
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Cone
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
- Pirâmides
Dada uma região poligonal de n vértices e um ponto V fora da região (outro plano), ao traçarmos segmentos de retas entre os vértices da região poligonal e o ponto V, construímos uma pirâmide que será classificada de acordo com o número de lados...
- Volume Do Tronco De Pirâmide
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.br www.accbarrosogestar.wordpress.comwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...