Matemática
Dada uma região poligonal de n vértices e um ponto V fora da região (outro plano), ao traçarmos segmentos de retas entre os vértices da região poligonal e o ponto V, construímos uma pirâmide que será classificada de acordo com o número de lados do polígono da base.
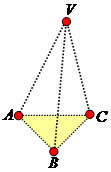
Os segmentos AV, BV e CV são as arestas laterais da pirâmide.
Os pontos A, B, C e V são os vértices.
Os triângulos VAB,VBC e VCA são as faces laterais.
O triângulo ABC é outra face da pirâmide e constitui a base.
A distância do ponto V ao centro da base constitui a altura da pirâmide.
A classificação de uma pirâmide depende do número de arestas da região da área da base.
Base é um triângulo
Nome: pirâmide triangular
Número de faces: três faces laterais mais face da base, portanto, quatro faces.
Base é um quadrado
Nome: pirâmide quadrangular
Número de faces: quatro faces laterais mais face da base, portanto, cinco faces.
Base é um pentágono
Nome: pirâmide pentagonal
Número de faces: cinco faces laterais mais face da base, portanto, seis faces.
Base é um hexágono
Nome: pirâmide de base hexagonal
Número de faces: seis faces laterais mais face da base, portanto, sete faces.
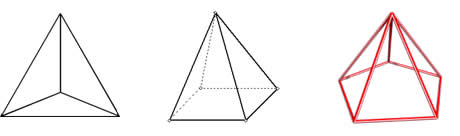
Pirâmide triangular Pirâmide quadrangular Pirâmide pentagonal
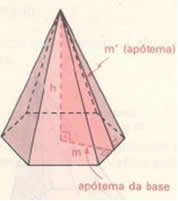
Altura, apótema da base e apótema da pirâmide
h: altura da pirâmide
m’: apótema da pirâmide
m: apótema da base
Pelo teorema de Pitágoras temos:
m’² = h² + m²
Área da base
A área da base de uma pirâmide depende da área do polígono em questão, sendo calculada pela expressão:
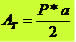
onde P: perímetro do polígono e a: apótema do polígono.
Área lateral
É a soma de todas as áreas laterais.
Área totalSoma da área lateral com a área da base.
At = Al + Ab
Volume
O volume de uma pirâmide é dado pela expressão:
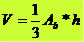
onde Ab: área da base (depende do polígono) e h: altura da pirâmide.
Planificação de uma pirâmide
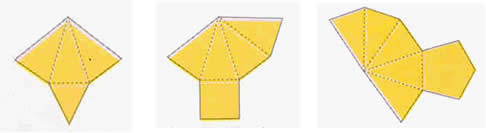
Pirâmide triangular Pirâmide quadrangular Pirâmide pentagonal
Marcos Noé
- Questão 28 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
Uma pirâmide possui 24 arestas. Pode-se concluir que se trata de uma pirâmide cuja base tem a forma de um (A) heptágono. (B) octógono. (C) eneágono. (D) decágono. (E) dodecágono. Solução: (E) Aplicando o Método de Resolução de Problemas...
- Questão 33 ? Processo De Promoção ? Professor De Matemática ? See ? São Paulo ? 2.013
A respeito de um prisma com 18 arestas e de uma pirâmide também com 18 arestas, é correto afirmar que (A) O prisma e a pirâmide têm, ambos, 12 vértices.(B) O prisma tem 12 vértices e a pirâmide tem 10 vértices.(C) O prisma tem 6 faces e a pirâmide...
- Concurso Público ? Professor De Educação Básica Ii ? Matemática
Concurso: Professor de Educação Básica II ? Matemática Ano: 2.012 Órgão: Prefeitura Municipal de Sertãozinho Instituição: Fundação Vunesp Questão: 47 Analise as seguintes afirmativas sobre prismas e pirâmides: I. um prisma com 24 arestas...
- Questão 52 ? Prova Do Estado ? (ofa) 2.013 ? Professor De Educação Básica Ii
Uma pirâmide tem 12 faces. É correto afirmar que o número de arestas dessa pirâmide é (A) 20. (B) 22. (C) 24. (D) 34. (E) 36. Solução: (B) Se a pirâmide possui 12 faces, logo: uma face é a base, sendo assim a base possui 11 lados (11 vértices...
- Pirâmides
Consideremos um polígono contido em um plano (por exemplo, o plano horizontal) e um ponto V localizado fora desse plano. Uma Pirâmide é a reunião de todos os segmentos que têm uma extremidade em P e a outra num ponto qualquer do polígono....
Matemática
Pirâmides
Dada uma região poligonal de n vértices e um ponto V fora da região (outro plano), ao traçarmos segmentos de retas entre os vértices da região poligonal e o ponto V, construímos uma pirâmide que será classificada de acordo com o número de lados do polígono da base.

Os segmentos AV, BV e CV são as arestas laterais da pirâmide.
Os pontos A, B, C e V são os vértices.
Os triângulos VAB,VBC e VCA são as faces laterais.
O triângulo ABC é outra face da pirâmide e constitui a base.
A distância do ponto V ao centro da base constitui a altura da pirâmide.
A classificação de uma pirâmide depende do número de arestas da região da área da base.
Base é um triângulo
Nome: pirâmide triangular
Número de faces: três faces laterais mais face da base, portanto, quatro faces.
Base é um quadrado
Nome: pirâmide quadrangular
Número de faces: quatro faces laterais mais face da base, portanto, cinco faces.
Base é um pentágono
Nome: pirâmide pentagonal
Número de faces: cinco faces laterais mais face da base, portanto, seis faces.
Base é um hexágono
Nome: pirâmide de base hexagonal
Número de faces: seis faces laterais mais face da base, portanto, sete faces.

Pirâmide triangular Pirâmide quadrangular Pirâmide pentagonal
Altura, apótema da base e apótema da pirâmide
h: altura da pirâmide
m’: apótema da pirâmide
m: apótema da base
Pelo teorema de Pitágoras temos:
m’² = h² + m²

Área da base
A área da base de uma pirâmide depende da área do polígono em questão, sendo calculada pela expressão:
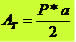
onde P: perímetro do polígono e a: apótema do polígono.
Área lateral
É a soma de todas as áreas laterais.
Área totalSoma da área lateral com a área da base.
At = Al + Ab
Volume
O volume de uma pirâmide é dado pela expressão:
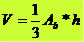
onde Ab: área da base (depende do polígono) e h: altura da pirâmide.
Planificação de uma pirâmide

Pirâmide triangular Pirâmide quadrangular Pirâmide pentagonal
Marcos Noé
- Questão 28 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
Uma pirâmide possui 24 arestas. Pode-se concluir que se trata de uma pirâmide cuja base tem a forma de um (A) heptágono. (B) octógono. (C) eneágono. (D) decágono. (E) dodecágono. Solução: (E) Aplicando o Método de Resolução de Problemas...
- Questão 33 ? Processo De Promoção ? Professor De Matemática ? See ? São Paulo ? 2.013
A respeito de um prisma com 18 arestas e de uma pirâmide também com 18 arestas, é correto afirmar que (A) O prisma e a pirâmide têm, ambos, 12 vértices.(B) O prisma tem 12 vértices e a pirâmide tem 10 vértices.(C) O prisma tem 6 faces e a pirâmide...
- Concurso Público ? Professor De Educação Básica Ii ? Matemática
Concurso: Professor de Educação Básica II ? Matemática Ano: 2.012 Órgão: Prefeitura Municipal de Sertãozinho Instituição: Fundação Vunesp Questão: 47 Analise as seguintes afirmativas sobre prismas e pirâmides: I. um prisma com 24 arestas...
- Questão 52 ? Prova Do Estado ? (ofa) 2.013 ? Professor De Educação Básica Ii
Uma pirâmide tem 12 faces. É correto afirmar que o número de arestas dessa pirâmide é (A) 20. (B) 22. (C) 24. (D) 34. (E) 36. Solução: (B) Se a pirâmide possui 12 faces, logo: uma face é a base, sendo assim a base possui 11 lados (11 vértices...
- Pirâmides
Consideremos um polígono contido em um plano (por exemplo, o plano horizontal) e um ponto V localizado fora desse plano. Uma Pirâmide é a reunião de todos os segmentos que têm uma extremidade em P e a outra num ponto qualquer do polígono....
