Matemática

Lista de Exercícios Preparatória para o Profmat

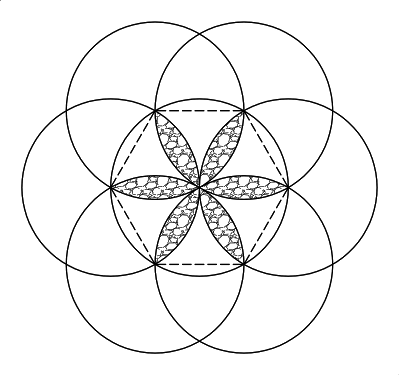
Um arquiteto desenhou a rosácea da figura, produzida por interseções de seis círculos de raios iguais centrados sobre os vértices de um hexágono regular inscrito num círculo de mesmo raio. O arquiteto pretende fazer o desenho de forma tal que os círculos tenham 10 m de raio, num grande paredão, e para calcular a tinta necessária precisa estimar a área da rosácea (que está sombreada no desenho). Entre as cinco alternativas abaixo, aquela que melhor estima a área da rosácea é:

(A) 50 m²

(B) 80 m²

(C) 110 m²

(D) 160 m²

(E) 310 m²

Solução: (C)

(I) Método

Observe o hexágono traçado na circunferência da esquerda na Figura 1. Perceba que ele divide uma pétala da rosácea ao meio.

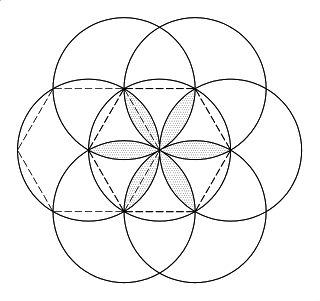Figura 1: Visualização da divisão da pétala da rosácea pelo hexágono.

A área da rosácea é o dobro da diferença da área do circulo, em que ela esta inscrita, pela área do hexágono regular inscrito na mesma circunferência.

A_{circunferência} = ? . r² , onde r é o raio da circunferência.

A_hexágono = [(3/2) . (a² . ?3)] , onde a é o lado do hexágono.

A_rosácea = 2 . (A_{circunferência} ? A_hexágono)

A_rosácea = 2 . {(? . r²) ? [(3/2) . (a² . ?3)]}

Como o hexágono está inscrito na circunferência a = r , então:

A_rosácea = 2 . {(? . r²) ? [(3/2) . (r² . ?3)]} = (2 . ? . r²) ? (3 . r² . ?3) =

= r² [(2 . ?) ? (3 . ?3)]

Considerando ? ? 3,14 e ?3 ? 1,73.

A_rosácea = r² [(2 . ?) ? (3 . ?3)] = 10² [(2 . 3,14) ? (3 . 1,73)] ? 103 m²

(II) Método

Observe a Figura 2. Cada pétala é formada por dois segmentos circulares e sua área é o dobro da diferença entre o setor circular pela área do triângulo equilátero contido neste setor.

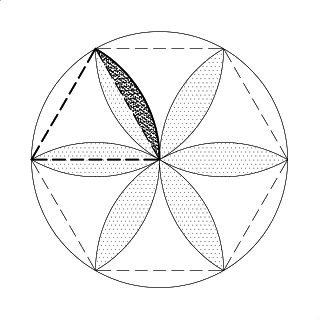Figura 2: Visualização do setor circular na rosácea.

A_triângulo = (a² . ?3) / 4 , onde a é o lado do triângulo equilátero.

A_{setor circular}= (? . r² . a) / 360º , onde a é o ângulo central e r é o raio da circunferência.

A_pétala = 2 . {[(? . r² . a) / 360] ? [(a² . ?3) / 4]}

O lado do triângulo equilátero é formado pelo raio da circunferência, então a = r.

A_pétala = 2 . {[(? . r² . a) / 360] ? [(r² . ?3) / 4]} =

= 2 . {[(? . r² . a) ? [90 . (r² . ?3)] / 360} = [(? . r² . a) ? [90 . (r² . ?3)] / 180

Considerando ? ? 3,14 e ?3 ? 1,73.

A_pétala = {(? . r² . 60) ? [90 . (r² . ?3)]} / 180 =

= {(3,14 . 10² . 6000) ? [(90 . (10² . 1,73)]} / 180 ? 18,17 m²

Como temos 6 pétalas

A_rosácea = 6 . A_pétala = 6 . 18,17 = 109,02 m²

Disponível em <http://www.profmat-sbm.org.br/default.asp>. Acessado em: 01 de fevereiro de 2.011.

- ResoluÇÃo Lista De ExercÍcios Profmat- Mestrado
Resolverei as questões da lista de exercícios disponibilizada no site http://www.profmat-sbm.org.br/docs/Lista_Problemas.pdf como estudo para a prova do Mestrado em Matemática. Questão 08 Um arquiteto desenhou a rosácea da figura, produzida por interseções...

- Questões Do Profmat
1Sérgio B. de Miranda1. Maria se exercita regularmente em sua bicicleta, por 30 minutos. Suameta, em cada sessão, é gastar, no mínimo, 420 kcal. Depois de seexercitar por 20 minutos, ela observa no mostrador que já gastou 240kcal. Para cumprir...

- Hexágono
Hexágono é uma figura plana que possui 6 lados, sendo regular esses lados deverão ser todos iguais (mesma medida), portanto, hexágono regular é uma figura plana que possui 6 lados com a mesma medida. O hexágono regular circunscrito numa circunferência...

- PolÍgonos Inscritos Na CircunferÊncia
Professor de Matemática e Ciências Antonio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] HTTP://ensinodematemtica.blogspot.com http://accbarrosogestar.blogspot.com.br I) RESUMO DE ALGUNS POLÍGONOS...

- Apótema
Considerando um círculo e um polígono inscrito de n lados, definimos como apótema de uma figura poligonal o segmento de reta que parte do centro da figura formando com o lado um ângulo de 90º, isto é, podemos dizer que o apótema é perpendicular...

Matemática