Matemática


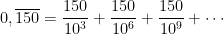
 .
.
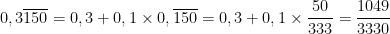 .
.


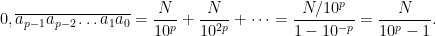
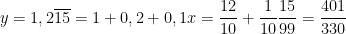 .
.
- Questão 21 ? Prova Do Estado ? (ofa) 2.013 ? Professor De Educação Básica Ii
Ao se utilizar uma calculadora com doze dígitos para dividir 1 por 253, o visor mostrará o valor 0,00395256917. Assim, é correto afirmar que (A) o número 1 / 253 não é racional, pois o quociente não é um número inteiro. (B) o número 1 / 253...
- ProgressÃo Geometrica
Progressão Geométrica (PG) é toda seqüência de números não nulos na qual é constante o quociente da divisão de cada termo (a partir do segundo) pelo termo anterior, esse quociente é chamado de razão (q) da progressão. • Seja a seqüência:...
- Conjunto
CONCEITO Conjunto vazio { } ou Ø: um conjunto que não possui elementos. Subconjuntos: quando todos os elementos de um conjunto A qualquer, pertencem a um outro conjunto B, pode-se dizer, então, que A é um subconjunto de B. Observações: - Todo o...
- Fração Geratriz
A fração geratriz, quando representada na forma decimal, produz dízimas periódicas simples ou compostas. Portanto, toda dízima periódica (número decimal) deve possuir uma forma fracionária, por isso demonstraremos como transformar números decimais...
- Dizimas
Dízimas periódicas Há frações que não possuem representações decimal exata. Por exemplo: Aos numerais decimais em que há repetição periódica e infinita de um ou mais algarismos, dá-se o nome de numerais decimais periódicos...
Matemática
Números Racionais: Dízimas Periódicas e Série Geométrica

Autor: Profº Americo Tavares - Site Teoremas e Problemas (Grifo Meu)
Exemplo: Prove que qualquer número representado por uma dízima periódica é racional.
Se considerar, como exemplo, o número 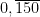 , em que a barra, nesta notação, significa que o grupo de
, em que a barra, nesta notação, significa que o grupo de 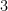 dígitos
dígitos  se repete indefinidamente:
se repete indefinidamente:
posso escrevê-lo na forma:
e calcular agora a soma da progessão geométrica de razão 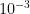 e primeiro termo 0,150
e primeiro termo 0,150
No segundo exemplo tomo o número 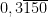 como ilustrativo do caso em que a dízima não começa imediatamente a seguir à vírgula. Assim, usando o resultado anterior:
como ilustrativo do caso em que a dízima não começa imediatamente a seguir à vírgula. Assim, usando o resultado anterior:
No último exemplo, considero  . Será:
. Será:
O caso geral é simplesmente o de uma dízima periódica com 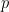 dígitos, bastando, como se viu, mostrar a propriedade para os números do tipo
dígitos, bastando, como se viu, mostrar a propriedade para os números do tipo 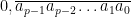 , porque os outros são uma consequência imediata.
, porque os outros são uma consequência imediata.
O número cujos dígitos são os que estão sob a barra tem o valor inteiro
Sendo assim, usando o mesmo raciocínio do primeiro exemplo, tem-se:
Exemplo de aplicação:
Para 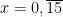 ,
,  De
De  deduz-se
deduz-se 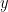
- Questão 21 ? Prova Do Estado ? (ofa) 2.013 ? Professor De Educação Básica Ii
Ao se utilizar uma calculadora com doze dígitos para dividir 1 por 253, o visor mostrará o valor 0,00395256917. Assim, é correto afirmar que (A) o número 1 / 253 não é racional, pois o quociente não é um número inteiro. (B) o número 1 / 253...
- ProgressÃo Geometrica
Progressão Geométrica (PG) é toda seqüência de números não nulos na qual é constante o quociente da divisão de cada termo (a partir do segundo) pelo termo anterior, esse quociente é chamado de razão (q) da progressão. • Seja a seqüência:...
- Conjunto
CONCEITO Conjunto vazio { } ou Ø: um conjunto que não possui elementos. Subconjuntos: quando todos os elementos de um conjunto A qualquer, pertencem a um outro conjunto B, pode-se dizer, então, que A é um subconjunto de B. Observações: - Todo o...
- Fração Geratriz
A fração geratriz, quando representada na forma decimal, produz dízimas periódicas simples ou compostas. Portanto, toda dízima periódica (número decimal) deve possuir uma forma fracionária, por isso demonstraremos como transformar números decimais...
- Dizimas
Dízimas periódicas Há frações que não possuem representações decimal exata. Por exemplo: Aos numerais decimais em que há repetição periódica e infinita de um ou mais algarismos, dá-se o nome de numerais decimais periódicos...
