Matemática
A Proposição $47$ do Livro $I$ dos Elementos de Euclides trata da demonstração do Teorema da Hipotenusa, o conhecido como Teorema de Pitágoras. Veremos neste artigo como Euclides conduziu sua demonstração.

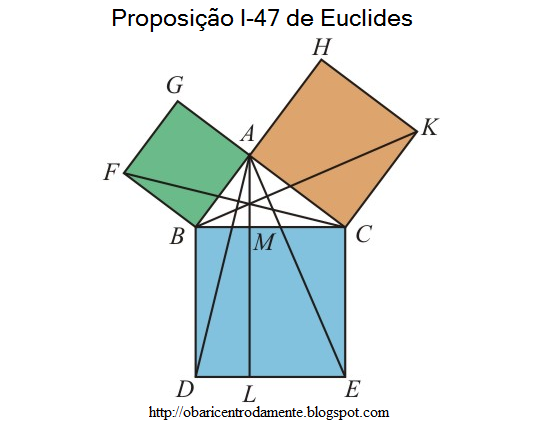
O cerne da demonstração consiste em estabelecer a igualdade entre o retângulo $BDLM$ e o quadrado $ABFG$.
Vejam que o triângulo $ABD$ e $BCF$ são iguais, pois os dois triângulos têm dois lados iguais com ângulos iguais e estes são a metade do retângulo $BDLM$. Esta igualdade entre triângulos já havia sido previamente estabelecida na proposição $I-4$ de seus Elementos:

Numa perspectiva moderna, a igualdade dos triângulos se dá pelo fato de que eles se deduzem um do outro por uma rotação de $90^\circ$. Mas de que modo Euclides justifica que o retângulo $BDLM$ seja o duplo do triângulo $ABD$?
Euclides utilizou-se de outra proposição já estabelecida num teorema mais geral, onde combina triângulos e paralelogramos:

Unindo $AL$, então os triângulo $ABC$ e $EBC$ tem mesma área, cujas bases $BC$ são iguais e estão nas mesmas paralelas $BC$ e $AE$. Logo $BCE$ é a metade de $ABCD$.
Para a prova deste teorema, Euclides une a diagonal $AC$, construindo o triângulo $ABC$, que também tem $BC$ como base, e enuncia duas asserções:
$1)$ Os triângulos $ABC$ e $EBC$, por terem mesma base e estarem nas mesmas paralelas são iguais.
$2)$ O triângulo $ABC$ é a metade do paralelogramo $ABCD$, porque $AC$ é a diagonal e porque a diagonal de um paralelogramo o divide em duas partes iguais.
Esta afirmação advém de outra proposição:

Desta forma, temos que provar que a $I-41$ se aplica na $I-47$. Vamos tomar o quadrado $ABFG$ e o triângulo $BCF$. Por construção $ABFG$ é um quadrado, logo os segmentos $BF$ e $AG$ são paralelos, assim como no retângulo $BDLM$ os segmentos $BD$ e $LM$ também são.
Basta, então, mostrar que o vértice c está sobre o prolongamento de $GA$. Euclides observa:
“Uma vez que cada um dos ângulos sob $BAC$ e $BAG$ é reto, relativamente à reta $BA$, os dois segmentos $AC$ e $AG$, não posicionados do mesmo lado, formam ângulos adjacentes iguais a dois retos. Portanto, $CA$ também está alinhado a $AH$”.
Desta forma, concluímos que o quadrado $ABFG$ tem a mesma base do triângulo $BCF$ e estão na mesma paralela $GC$. Daqui vem que o quadrado $ABFG$ é o duplo do triângulo $BCF$. Mas os triângulos $BCF$ e $ABD$ são iguais, o que nos leva à igualdade entre o quadrado $ABFG$ e o retângulo $BDLM$.
De modo análogo provamos que o quadrado $ACKH$ é igual ao retângulo $CELM$.
Assim, a reunião dos retângulos $BDLM$ e $CELM$ constituem o grande quadrado $BDEC$ sobre a hipotenusa $BC$, e este haverá de ser igual aos dois quadrados $ABFG$ e $ACKH$.
[2] Os Elementos - Euclides - Tradução de Irineu Bicudo - Ed. Unesp
[3] ttp://aleph0.clarku.edu/~djoyce/java/elements/toc.html
O teorema de Pitágoras baseado nas relações métricas da circunferência
Uma demonstração do teorema pitagórico segundo Euclides no blog TICs na Matemática
Provas do Teorema de Pitágoras no Blog Fatos Matemáticos Parte 1, 2, 3, 4, 5

- Triângulo Retângulo
Todo triângulo que tem um ângulo de 90°(ângulo reto) é denominado triângulo retângulo. O triângulo ABC tem um ângulo reto e é denominado triângulo retângulo: Onde: a: hipotenusa; b e c: catetos; h: altura relativa à hipotenusa; m e n: projeções...
- Relações Métricas Triângulo Retângulo
Num triângulo retângulo, os lados perpendiculares, aqueles que formam um ângulo de 90º, são denominados catetos e o lado oposto ao ângulo de 90º recebe o nome de hipotenusa. O teorema de Pitágoras é aplicado ao triângulo retângulo e diz que:...
- Triângulo
O triângulo é considerado uma importante figura no ramo da Geometria, pois através dele podemos estabelecer várias relações fundamentais, como exemplo temos uma relação muito importante utilizada na Geometria e na Trigonometria, que é o Teorema...
- Relações Métricas Triângulo Retângulo
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
- Quadriláteros Notáveis
A Geometria que hoje estudamos teve sua origem aproximadamente a 300 a.C., por Euclides em sua obra Os Elementos, dividido em treze livros. Na definição 19 do Livro I, Euclides define uma “figura quadrilátera” como sendo aquela contida por quatro...
Matemática
O teorema de Pitágoras, segundo Euclides – A proposição $I-47$
A Proposição $47$ do Livro $I$ dos Elementos de Euclides trata da demonstração do Teorema da Hipotenusa, o conhecido como Teorema de Pitágoras. Veremos neste artigo como Euclides conduziu sua demonstração.

Proposição $I-47$
Em um triângulo retângulo, o quadrado sobre o lado oposto ao ângulo reto é igual à soma dos quadrados sobre os lados que forma o ângulo reto.
O cerne da demonstração consiste em estabelecer a igualdade entre o retângulo $BDLM$ e o quadrado $ABFG$.
Vejam que o triângulo $ABD$ e $BCF$ são iguais, pois os dois triângulos têm dois lados iguais com ângulos iguais e estes são a metade do retângulo $BDLM$. Esta igualdade entre triângulos já havia sido previamente estabelecida na proposição $I-4$ de seus Elementos:
Proposição $I-4$
Se dois triângulo tem dois lados iguais a dois, respectivamente, e se o ângulo contido por estes dois lados forem iguais, então eles também têm suas bases iguais. Consequentemente os triângulos serão iguais e os ângulos restantes também serão.
Numa perspectiva moderna, a igualdade dos triângulos se dá pelo fato de que eles se deduzem um do outro por uma rotação de $90^\circ$. Mas de que modo Euclides justifica que o retângulo $BDLM$ seja o duplo do triângulo $ABD$?
Euclides utilizou-se de outra proposição já estabelecida num teorema mais geral, onde combina triângulos e paralelogramos:
Proposição $I-41$
Se um paralelogramo tem a mesma base que um triângulo e estes estão na mesma paralela, então o paralelogramo é o dobro do triângulo.
Unindo $AL$, então os triângulo $ABC$ e $EBC$ tem mesma área, cujas bases $BC$ são iguais e estão nas mesmas paralelas $BC$ e $AE$. Logo $BCE$ é a metade de $ABCD$.
Para a prova deste teorema, Euclides une a diagonal $AC$, construindo o triângulo $ABC$, que também tem $BC$ como base, e enuncia duas asserções:
$1)$ Os triângulos $ABC$ e $EBC$, por terem mesma base e estarem nas mesmas paralelas são iguais.
$2)$ O triângulo $ABC$ é a metade do paralelogramo $ABCD$, porque $AC$ é a diagonal e porque a diagonal de um paralelogramo o divide em duas partes iguais.
Esta afirmação advém de outra proposição:
Proposição $I-34$
Em áreas paralelogrâmicas os lados e os ângulos opostos são iguais entre si e a diagonal divide as áreas e, partes iguais.
Desta forma, temos que provar que a $I-41$ se aplica na $I-47$. Vamos tomar o quadrado $ABFG$ e o triângulo $BCF$. Por construção $ABFG$ é um quadrado, logo os segmentos $BF$ e $AG$ são paralelos, assim como no retângulo $BDLM$ os segmentos $BD$ e $LM$ também são.
Basta, então, mostrar que o vértice c está sobre o prolongamento de $GA$. Euclides observa:
“Uma vez que cada um dos ângulos sob $BAC$ e $BAG$ é reto, relativamente à reta $BA$, os dois segmentos $AC$ e $AG$, não posicionados do mesmo lado, formam ângulos adjacentes iguais a dois retos. Portanto, $CA$ também está alinhado a $AH$”.
Desta forma, concluímos que o quadrado $ABFG$ tem a mesma base do triângulo $BCF$ e estão na mesma paralela $GC$. Daqui vem que o quadrado $ABFG$ é o duplo do triângulo $BCF$. Mas os triângulos $BCF$ e $ABD$ são iguais, o que nos leva à igualdade entre o quadrado $ABFG$ e o retângulo $BDLM$.
De modo análogo provamos que o quadrado $ACKH$ é igual ao retângulo $CELM$.
Assim, a reunião dos retângulos $BDLM$ e $CELM$ constituem o grande quadrado $BDEC$ sobre a hipotenusa $BC$, e este haverá de ser igual aos dois quadrados $ABFG$ e $ACKH$.
Referências:
[1] Revista Scientific American – A Ciência na Antiguidade, Nº 3[2] Os Elementos - Euclides - Tradução de Irineu Bicudo - Ed. Unesp
[3] ttp://aleph0.clarku.edu/~djoyce/java/elements/toc.html
Veja mais:
Os Elementos de EuclidesO teorema de Pitágoras baseado nas relações métricas da circunferência
Uma demonstração do teorema pitagórico segundo Euclides no blog TICs na Matemática
Provas do Teorema de Pitágoras no Blog Fatos Matemáticos Parte 1, 2, 3, 4, 5

- Triângulo Retângulo
Todo triângulo que tem um ângulo de 90°(ângulo reto) é denominado triângulo retângulo. O triângulo ABC tem um ângulo reto e é denominado triângulo retângulo: Onde: a: hipotenusa; b e c: catetos; h: altura relativa à hipotenusa; m e n: projeções...
- Relações Métricas Triângulo Retângulo
Num triângulo retângulo, os lados perpendiculares, aqueles que formam um ângulo de 90º, são denominados catetos e o lado oposto ao ângulo de 90º recebe o nome de hipotenusa. O teorema de Pitágoras é aplicado ao triângulo retângulo e diz que:...
- Triângulo
O triângulo é considerado uma importante figura no ramo da Geometria, pois através dele podemos estabelecer várias relações fundamentais, como exemplo temos uma relação muito importante utilizada na Geometria e na Trigonometria, que é o Teorema...
- Relações Métricas Triângulo Retângulo
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
- Quadriláteros Notáveis
A Geometria que hoje estudamos teve sua origem aproximadamente a 300 a.C., por Euclides em sua obra Os Elementos, dividido em treze livros. Na definição 19 do Livro I, Euclides define uma “figura quadrilátera” como sendo aquela contida por quatro...
