Matemática
Num triângulo retângulo, os lados perpendiculares, aqueles que formam um ângulo de 90º, são denominados catetos e o lado oposto ao ângulo de 90º recebe o nome de hipotenusa. O teorema de Pitágoras é aplicado ao triângulo retângulo e diz que: hipotenusa ao quadrado é igual à soma dos quadrados dos catetos, hip² = c² + c².

- Questão 59 ? Processo De Promoção ? Professor De Matemática ? See ? São Paulo ? 2.013
A professora do 9.º ano solicitou a seus alunos que localizassem na reta numérica o ponto correspondente a 2 ?3, utilizando régua e compasso. Todos os alunos tinham bons instrumentos e fizeram os transportes das medidas adequadamente, utilizando de...
- Triângulo Retângulo
Todo triângulo que tem um ângulo de 90°(ângulo reto) é denominado triângulo retângulo. O triângulo ABC tem um ângulo reto e é denominado triângulo retângulo: Onde: a: hipotenusa; b e c: catetos; h: altura relativa à hipotenusa; m e n: projeções...
- Relações Métricas No Triângulo Retângulo
Relações métricas no triângulo retânguloMarcelo Rigonatto Triângulo retânguloO triângulo é o polígono com menor número de lados, mas é uma das formas geométricas mais importantes no estudo da geometria. Sempre intrigou...
- Relações Métricas Triângulo Retângulo
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
- Triângulo Retângulo Exercícios
c² = a.n b² = a.m h² = m.n c.b = a.h c² + b² = a² Exercícios sobre Relações Métricas no Triângulo Retângulo. 1. Em um triângulo retângulo as projeções dos catetos sobre a hipotenusa medem 6 cm e 8 cm. Determine a altura relativa à hipotenusa...
Matemática
Relações Métricas Triângulo retângulo
Num triângulo retângulo, os lados perpendiculares, aqueles que formam um ângulo de 90º, são denominados catetos e o lado oposto ao ângulo de 90º recebe o nome de hipotenusa. O teorema de Pitágoras é aplicado ao triângulo retângulo e diz que: hipotenusa ao quadrado é igual à soma dos quadrados dos catetos, hip² = c² + c².

Relações métricas no triângulo retângulo
Observe os triângulos:
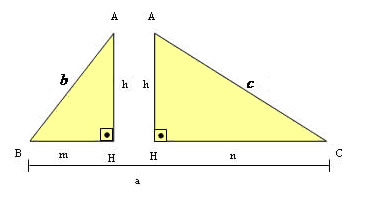
Os triângulos AHB e AHC são semelhantes, então podemos estabelecer algumas relações métricas importantes:
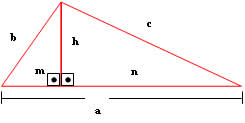
h² = mn b² = na c² = am bc = ah
Aplicações do Teorema de Pitágoras
Diagonal do quadrado
Dado o quadrado de lado l, a diagonal D do quadrado será a hipotenusa de um triângulo retângulo com catetos l, com base nessa definição usaremos o teorema de Pitágoras para uma expressão que calcula a diagonal do quadrado em função da medida do lado.
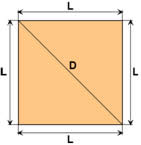
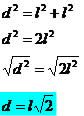
Altura de um triângulo equilátero
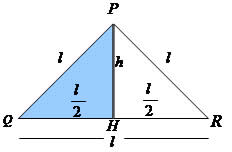
O triângulo PQR é equilátero, vamos calcular sua altura com base na medida l dos lados. Ao determinarmos a altura (h) do triângulo PQR, podemos observar um triângulo retângulo PHQ catetos: h e l/2 e hipotenusa h. Aplicando o teorema de Pitágoras temos:
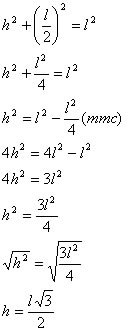
Diagonal do bloco retangular (paralelepípedo)
Observe o bloco de arestas a, b e c, iremos calcular a diagonal (d), mas usaremos a diagonal x da base em nossos cálculos. Veja:
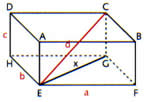
x² = a² + b²
d² = x² + c²
substituindo, temos:
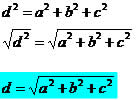
Diagonal do cubo (caso particular do paralelepípedo)
Consideremos o cubo um caso particular de um bloco retangular, então:
a = b = c = l
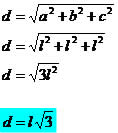
Observe os triângulos:

Os triângulos AHB e AHC são semelhantes, então podemos estabelecer algumas relações métricas importantes:

h² = mn b² = na c² = am bc = ah
Aplicações do Teorema de Pitágoras
Diagonal do quadrado
Dado o quadrado de lado l, a diagonal D do quadrado será a hipotenusa de um triângulo retângulo com catetos l, com base nessa definição usaremos o teorema de Pitágoras para uma expressão que calcula a diagonal do quadrado em função da medida do lado.

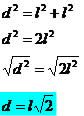
Altura de um triângulo equilátero
O triângulo PQR é equilátero, vamos calcular sua altura com base na medida l dos lados. Ao determinarmos a altura (h) do triângulo PQR, podemos observar um triângulo retângulo PHQ catetos: h e l/2 e hipotenusa h. Aplicando o teorema de Pitágoras temos:

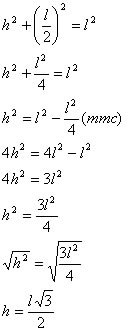
Diagonal do bloco retangular (paralelepípedo)
Observe o bloco de arestas a, b e c, iremos calcular a diagonal (d), mas usaremos a diagonal x da base em nossos cálculos. Veja:

x² = a² + b²
d² = x² + c²
substituindo, temos:
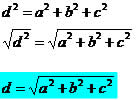
Diagonal do cubo (caso particular do paralelepípedo)
Consideremos o cubo um caso particular de um bloco retangular, então:
a = b = c = l
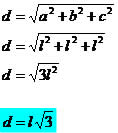
fonte : http://matematica--devrev.blogspot.com
- Questão 59 ? Processo De Promoção ? Professor De Matemática ? See ? São Paulo ? 2.013
A professora do 9.º ano solicitou a seus alunos que localizassem na reta numérica o ponto correspondente a 2 ?3, utilizando régua e compasso. Todos os alunos tinham bons instrumentos e fizeram os transportes das medidas adequadamente, utilizando de...
- Triângulo Retângulo
Todo triângulo que tem um ângulo de 90°(ângulo reto) é denominado triângulo retângulo. O triângulo ABC tem um ângulo reto e é denominado triângulo retângulo: Onde: a: hipotenusa; b e c: catetos; h: altura relativa à hipotenusa; m e n: projeções...
- Relações Métricas No Triângulo Retângulo
Relações métricas no triângulo retânguloMarcelo Rigonatto Triângulo retânguloO triângulo é o polígono com menor número de lados, mas é uma das formas geométricas mais importantes no estudo da geometria. Sempre intrigou...
- Relações Métricas Triângulo Retângulo
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
- Triângulo Retângulo Exercícios
c² = a.n b² = a.m h² = m.n c.b = a.h c² + b² = a² Exercícios sobre Relações Métricas no Triângulo Retângulo. 1. Em um triângulo retângulo as projeções dos catetos sobre a hipotenusa medem 6 cm e 8 cm. Determine a altura relativa à hipotenusa...
